
- •Вопросы к экзамену по математическому анализу.
- •1.Определение определенного интеграла.
- •2.Необходимое условие существования определенного интеграла
- •3. Нижняя и верхняя интегральные суммы Дарбу и их свойства.
- •4. Необходимое и достаточное условие существования определенного интеграла.
- •5. Некоторые классы функций для которых существует определенный интеграл
- •6. Некоторые свойства определённого интеграла
- •7.Определение интеграла с переменным верхним пределом.
- •8.Опредидение интеграла с переменным верхним пределом.
- •9. Формула Ньютона-Лейбница.
- •10. Замена переменной в определённом интеграле
- •11. Интегрирование по частям в определенном интеграле
- •12. Понятие квадрируемой фигуры и её площади.
- •13. Свойства квадрируемых фигур.
- •14. Понятие спрямляемой плоской кривой и её длины. Достаточное условие спрямляемости плоской кривой(сформулировать теорему).
- •15. Вычисление объёма тела вращения(с рисунком).
- •16.Вычисление площади поверхности вращения.
- •17. Определение несобственного интеграла первого рода и его свойства.
- •18. Определение несобственного интеграла второго рода и его свойства.
- •19. Понятие n-мерного Евклидова пространства.
- •20. Множества в пространстве .
- •21. Понятие действительной функции нескольких действительных переменных.
- •22. Действительная функция двух действительных переменных.
- •23. Предел функции двух действительных переменных . Повторные пределы.
- •24. Непрерывность функции двух действительных переменных.
- •25. Определение частной производной функции двух переменных. Механический смысл.
- •26. Определение дифференцируемой функции двух действительных переменных и полного дифференциала. Необходимое условие дифференцируемости функции двух действительных переменных.
- •27. Достаточное условие дифференцируемости двух действительных переменных.
- •28.Дифференцирование сложной функции.
- •29. Частные производные высших порядков.
- •30. Восстановление функции по её полному дифференциалу.
- •31. Дифференциалы высших порядков для функции двух переменных.
- •32. Определение производной по направлению. Теорема.
- •33. Градиент функции. И его свойства.
20. Множества в пространстве .
Определение:
Пусть
точка
 тогда множество точек
тогда множество точек
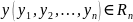 удовлетворяющих неравенству
удовлетворяющих неравенству
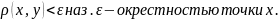
Обозначают:
 .
.
Определение:
Точка
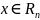 называется внутренней
точкой
множества M
называется внутренней
точкой
множества M ,
если точка входит в множество М вместе
с некоторой Е окрестностью.
,
если точка входит в множество М вместе
с некоторой Е окрестностью.
Определение:
Множество M ,
называется открытым
если все
его точки внутренние.
,
называется открытым
если все
его точки внутренние.
Определение: Точка х пространства называется предельной точкой множества M , если любая Е окрестность этой точки содержит бесконечно много точек из множества М.
Определение: Множество М называется замкнутым если оно содержит все свои предельные точки.
Определение: Всякое открытое множество M содержащее точку х называется просто окрестностью точки х.
Определение: Множество M называется связным, если любые две точки этого множества можно соединить непрерывной кривой целиком принадлежащей данному множеству.
Определение: Если множество пространства одновременно и открыто и связно, то такое множество называется областью.
В дальнейшем области будем обозначать: Д, ….
Определение: Точка называется граничной точкой области Д , если любая окрестность этой точки содержит как точки области Д, так и точки не принадлежащие ей. Множество граничных точек области Д называют границей области Д.
Определение: Если точкам области Д присоединить все граничные точки, то получим множество которое называется замкнутой областью Д.
Определение: Область Д называется ограниченной, если её можно заключить в шар конечного радиуса.
21. Понятие действительной функции нескольких действительных переменных.
Пусть Д это некоторое
множество точек пространства
.
И пусть каждой точке
 по некоторому правилу (закону) f
ставится в соответствие некоторое
действительное число
по некоторому правилу (закону) f
ставится в соответствие некоторое
действительное число
 ,тогда
говорят что на множестве Д определена
функция
,тогда
говорят что на множестве Д определена
функция
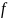 принимающая значение в пространстве
принимающая значение в пространстве
 .
Эту функцию называют
действительной функцией
.
Эту функцию называют
действительной функцией
 действительных
переменных
действительных
переменных
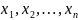 и обозначают
и обозначают
 ,
где
,
где
 ,
,
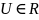 ,
или
,
или

Множество Д называют
областью определения функции, множество
чисел
 называют множеством значений функции.
Координаты
называют аргументами или независимыми
переменными.
называют множеством значений функции.
Координаты
называют аргументами или независимыми
переменными.
Чтобы задать функцию нужно
1. Задать область определения.
2.
Задать закон
ставящий в соответствие каждой точке
 некоторое действительное число
.
Из определения следует что функция f
является однозначной.
некоторое действительное число
.
Из определения следует что функция f
является однозначной.
22. Действительная функция двух действительных переменных.
Эта функция имеет вид:

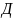 –
это область
определения функции.
–
это область
определения функции.
 – независимые
переменные.
– независимые
переменные.
Определение:
Линией
уровня для функции
 называется множество точек
называется множество точек
 в которых функция принимает одно и то
же значение.
в которых функция принимает одно и то
же значение.
Уравнение линии
уровня :
 постоянная.
постоянная.
