14. Понятие спрямляемой плоской кривой и её длины. Достаточное условие спрямляемости плоской кривой(сформулировать теорему).

Пусть плоская Жорданова кривая L задана параметрическими уравнениями . Пусть 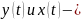непрерывны на отрезке

Отрезок произвольно разобьём на n частей точками .

Каждому значению на кривой соответствует

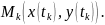
Соединим точки последовательно отрезками, получим ломаную линию, вписанную в кривую обозначим её через (Р). Таких ломаных можно вписать в кривую бесконечное множество. Обозначим {p} – множество длин вписанных в прямую ломанных (Р).

Определение: Если множество {P} – длин ломаных вписанных в прямую ограничено сверху то кривую называют спрямляемой кривой, а верхнюю грань {P}называют длиной кривой ). Будем обозначать длину кривой через .

По определению:

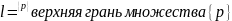
Определение: Жорданова кривая 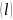задана параметрическими уравнениями

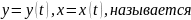регулярной кривой, если функции

и их производные 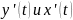непрерывны на отрезке

Регулярная кривая является кусочно-гладкой кривой.

Теорема: (достаточное условие) Если кривая - регулярна, то она спрямляема, то есть имеет длину.

15. Вычисление объёма тела вращения(с рисунком).

Пусть криволинейная трапеция ограниченная кривой 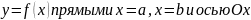вращается вокруг оси . Нужно вычислить объём тела полученного при вращении.

Объём будем обозначать отрезок произвольно разобъём на n частей точками

Через каждую точку проведём плоскость В результате тело разобъётся на n слоёв. Произвольно на каждом отрезке выберем и 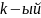слой заменим цилиндром с радиусом основания и высотой

Тогда объём к-ого цилиндра будет = .

Просуммировав эти объёмы по всем от 0 до 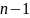получим объём тел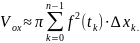а , Сумма Является интегральной суммой для функции переходя к пределу получаем точный объём тела 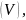а с другой стороны

Окончательно получим: ;

Пусть теперь криволинейная трапеция ограничена графиком функции 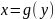прямыми и осью вращаются вокруг .

Тогда объём тела вращения находится по формуле: ;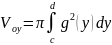

16.Вычисление площади поверхности вращения.

Пусть кривая является графиком функции 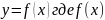непрерывно дифференцируема на отрезке [a,b]. И пусть вращается вокруг оси Ox.

Получим поверхность вращения, площадь которой надо вычислить. Площадь будем обозначать через

Отрезок произвольно разобъём на n частей точками

Через каждую точку проведём плоскость . Длина

будет 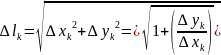²

Заменив отрезком получим усечённый конус площадь боковой поверхности которого находится по формуле:

Если то поэтому 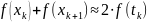тогда получим 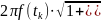² это площадь боковой поверхности к-ого усечённого конуса. Просуммировав эти площади по всем от 0 до получим площадь поверхности вращения :

Аналогично, если кривая вращается вокруг оси то площадь поверхности: