10. Замена переменной в определённом интеграле

Теорема: пусть требуется вычислить где функция f(x) непрерывна на отрезке . Вместо переменной введём переменную по формуле , где функция непрерывно дифференцируема на отрезке , её значение не выходят за пределы отрезка и при этом , тогда справедлива формула

= .

Замечание: применяя формулу замены переменной в неопределённом интеграле мы после отыскания первообразной, возвращались к старой переменной , в определённом интеграле этого делать не надо.

Замечание: часто вместо замены переменной на переменную по формуле , будем делать замену переменной на переменную по формуле

11. Интегрирование по частям в определенном интеграле

Пусть функции , непрерывно дифференцируемы на отрезке . Найдём дифференциал произведения этих функций:

Интегрируем это равенство на отрезке

по формуле Ньютона-Лейбница получим:

_a^b, получим

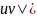_a^b= + следовательно

= _a^b- . – формула интегрирования по частям в определенном интеграле

12. Понятие квадрируемой фигуры и её площади.

Определение. Если то фигура (р) называется квадрируемой фигурой, а число (Р) называется площадью этой фигуры.

- внутренняя площадь фигуры (Р);

- внешняя площадь фигуры (Р);

- плоская фигура ограниченная некоторой непрерывной замкнутой линией.

Теорема: Для того чтобы фигура (Р) была квадрируемой , имела площадь необходимо и достаточно чтобы нашлись 2 многогранника(А) и (В) таких что В-А< где А и В – площади многоугольников (А) и (В).

Из теоремы следует что если фигура (Р) квадрируема, то её границу(L) можно заключить в многоугольник сколько угодно малой площади, и наоборот.

Определение: Говорят что кривая (L) имеет площадь равную нулю, если эту кривую можно заключить в многоугольник сколь угодно малой площади. Тогда предыдущая теорема формулируется так:

Теорема: Для того чтобы фигура (Р) была квадрируемой необходимо и достаточно чтобы её граница (L) имела площадь равную нулю.

Теорема: Пусть кривая (L) является графиком функции которая непрерывна на отрезке [a,b], тогда кривая (L) имеет площадь равную нулю.

13. Свойства квадрируемых фигур.

1. Свойство монотонности. Пусть фигуры (Р) и (Q) квадрируемы, и при этом фигура (Р) содержится в фигуре (Q) тогда

2. Свойство аддитивности. Пусть ( ) и ( ) это квадрируемые фигуры, и пусть (Р) будет равно ( ) и при этом ( ) в пересечении с ( ) не имеет общей площади тогда .