
- •Вопросы к экзамену по математическому анализу.
- •1.Определение определенного интеграла.
- •2.Необходимое условие существования определенного интеграла
- •3. Нижняя и верхняя интегральные суммы Дарбу и их свойства.
- •4. Необходимое и достаточное условие существования определенного интеграла.
- •5. Некоторые классы функций для которых существует определенный интеграл
- •6. Некоторые свойства определённого интеграла
- •7.Определение интеграла с переменным верхним пределом.
- •8.Опредидение интеграла с переменным верхним пределом.
- •9. Формула Ньютона-Лейбница.
- •10. Замена переменной в определённом интеграле
- •11. Интегрирование по частям в определенном интеграле
- •12. Понятие квадрируемой фигуры и её площади.
- •13. Свойства квадрируемых фигур.
- •14. Понятие спрямляемой плоской кривой и её длины. Достаточное условие спрямляемости плоской кривой(сформулировать теорему).
- •15. Вычисление объёма тела вращения(с рисунком).
- •16.Вычисление площади поверхности вращения.
- •17. Определение несобственного интеграла первого рода и его свойства.
- •18. Определение несобственного интеграла второго рода и его свойства.
- •19. Понятие n-мерного Евклидова пространства.
- •20. Множества в пространстве .
- •21. Понятие действительной функции нескольких действительных переменных.
- •22. Действительная функция двух действительных переменных.
- •23. Предел функции двух действительных переменных . Повторные пределы.
- •24. Непрерывность функции двух действительных переменных.
- •25. Определение частной производной функции двух переменных. Механический смысл.
- •26. Определение дифференцируемой функции двух действительных переменных и полного дифференциала. Необходимое условие дифференцируемости функции двух действительных переменных.
- •27. Достаточное условие дифференцируемости двух действительных переменных.
- •28.Дифференцирование сложной функции.
- •29. Частные производные высших порядков.
- •30. Восстановление функции по её полному дифференциалу.
- •31. Дифференциалы высших порядков для функции двух переменных.
- •32. Определение производной по направлению. Теорема.
- •33. Градиент функции. И его свойства.
6. Некоторые свойства определённого интеграла
1)

2)
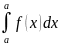 =0.
=0.
3)
 =
= .
.
4)
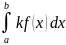 =k
.
=k
.
5) =
±
=
± .
.
6) если
 ,
тогда
,
тогда
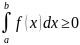
7) если
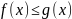 на отрезке
,то
на отрезке
,то
 .
.
8) если существует
,
то существует
 и при этом
и при этом
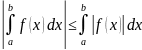 .
.
9) пусть
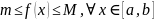 ,
тогда
,
тогда

10)
 справедливо равенство
справедливо равенство
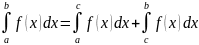
11) теорема о среднем значении функции
пусть
,
тогда найдется число
 ,
m≤µ≤M,
что будет выполнятся равенство
,
m≤µ≤M,
что будет выполнятся равенство

7.Определение интеграла с переменным верхним пределом.
Теорема о непрерывности
Пусть существует
,
тогда он будет существовать согласно
свойства 10 на любом отрезке
 где
где
 ,
получим интеграл
,
получим интеграл
 ,
,
если x изменяется от а до b, то значение этого интеграла будет меняться, получим функцию
 ,
где
,
,
где
,
функцию
 называют интегралом
с переменным верхним пределом.
называют интегралом
с переменным верхним пределом.
Теорема о непрерывности функции:
если функция f(x) интегрируема на отрезке , то функция непрерывна на отрезке .
Доказательство.
Воспользуемся
определением непрерывности функции в
виде:
Пусть х- любая
точка отрезка [a,b].
Точке х дадим приращение
 получим точку х+
получим точку х+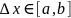 .
Запишем приращение функции
.
Запишем приращение функции

Тогда
 по
определениюФ(х) непрерывна в точке х.
Так как х произвольная точка отрезка
[a,b]
то Ф(х) непрерывна на отрезке [a,b].
по
определениюФ(х) непрерывна в точке х.
Так как х произвольная точка отрезка
[a,b]
то Ф(х) непрерывна на отрезке [a,b].
Доказано.
8.Опредидение интеграла с переменным верхним пределом.
Теорема о дифференцируемости
Пусть существует , тогда он будет существовать согласно свойства 10 на любом отрезке где , получим интеграл
,
если x изменяется от а до b, то значение этого интеграла будет меняться, получим функцию
, где ,
функцию называют интегралом с переменным верхним пределом.
Теорема о дифференцируемости:
если функция
непрерывна на отрезке
,
то функция
дифференцируема на отрезке
и при этом
 .
.
Доказательство.
Так как
непрерывна на отрезке [a,b],
то
 .
По определению производной Ф’(x)=
.
По определению производной Ф’(x)= так как
так как то при
то при
 окончательно
получим Ф’(x)=f(x),
окончательно
получим Ф’(x)=f(x),

Доказано.
Ф’(x)=f(x) означает что Ф(x) является первообразной для функции f(x) на отрезке [a,b] поэтому эту теорему называют ещё и теоремой существования первообразной для непрерывной функции.
9. Формула Ньютона-Лейбница.
Пусть функция
непрерывна на отрезке
,
тогда согласно предыдущей теоремы (о
дифференцируемости функции
 ) для неё существует первообразная
функции на отрезке
,
а именно
) для неё существует первообразная
функции на отрезке
,
а именно

Пусть
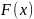 – какая-нибудь другая первообразная
для функции
– какая-нибудь другая первообразная
для функции
 Первообразные
и
Первообразные
и
 отличаются друг от друга на постоянную
С,
отличаются друг от друга на постоянную
С,
 ,
или
,
или

Найдём значение С.
Пусть x=a,
получим
 так как
так как
 Тогда
Тогда

Пусть x=b,
получим
 Формула
Ньютона-Лейбница.
Формула
Ньютона-Лейбница.
Обозначим
 ab
ab
В окончательном виде получим формулу Ньютона-Лейбница –
 ab
ab
Чтобы вычислить
определённый интеграл с помощью формулы
Ньютона-Лейбница нужно каким-то образом
найти какую-нибудь первообразную функции
f(x),
а затем найти разность

