2.Необходимое условие существования определенного интеграла
Теорема:
Для существования определённого
интеграла необходимо чтобы функция
была ограничена на отрезке
.
Доказательство. От противного.
Пусть функция
неограничена в какой-нибудь точке
отрезка [a,b]
тогда эта точка будет принадлежать
одному из отрезков
и поэтому мы можем точки
выбирать сколько угодно близко к данной
точке и соответствующую сумму
можем сделать сколь угодно большой.
Исходя из этого можно построить
последовательность, которая неограниченно
возрастает, тоесть
. Но по определению определённого
интеграла требуется чтобы предел был
конечным, следовательно, получили
противоречие. Следовательно,
для неограниченной функции определённый
интеграл не существует.
Доказано.
3. Нижняя и верхняя интегральные суммы Дарбу и их свойства.
Пусть функция
ограничена на отрезке
,
тогда она будет ограничена на каждом
отрезке
,
,
,
где
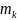и
- нижняя и верхняя грани функции на
отрезке
.
Запишем суммы
,
Эти суммы называют соответственно нижней и верхней интегральными сумами Дарбу на отрезке .
Свойства интегральных сумм Дарбу:
Свойство 1:
если к имеющимся точкам отрезка [a,b]
добавить хотя бы одну точку, то от этого
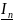может лишь увеличиться, а
- уменьшится.
Свойство 2: всякая нижняя интегральная сумма Дарбу не превосходит всякой верхней интегральной сумме Дарбу, даже если эти суммы построены по различном разбиении отрезка .
4. Необходимое и достаточное условие существования определенного интеграла.
Теорема:
для того чтобы существовал определенный
интеграл
необходимо и достаточно чтобы
.
Доказательство.
Необходимость.
Пусть существует
это значит что
что если
выполняется неравенство
то выполняется неравенство
и
нижние и верхние грани множества
интегральных сумм
То есть
то
и
Вычитая из второго равенства первое
получим
.
Достаточность.
Пусть
то есть
Так как
и
то есть
А предел слева – это определённый
интеграл
Доказано.
Равенство запишем по-другому:
,
– колебание функции
на отрезке
и тогда
получим:
Теорема: для того чтобы существовал определенный интеграл необходимо и достаточно чтобы
5. Некоторые классы функций для которых существует определенный интеграл
Теорема:
если функция
непрерывна на
отрезке [a,b],
то для неё существует определенный
интеграл.
Доказательство.
Так
как по условию f(x)
непрерывна на отрезке [a,b]
то по следствию к теореме Кантора
Такое,
что если отрезок разбить на отрезки с
длинами меньшими чем
,
то колебания функции f(x)
на каждом из отрезков разбиения будет
меньше
Получим 0
следовательно выполняется условие
предыдущей теоремы и следовательно
функция интегрируема на отрезке [a,b],
то есть существует
.
Доказано.
Теорема: если функция ограничена и монотонна на отрезке , то для неё существует определенный интеграл.
Теорема: если функция ограничена на отрезке , имеет конечное число точек разрыва , то для неё существует определенный интеграл.