Вопрос 8. Линейные однородные дифференциальные уравнения.

Общее решение линейных уравнений можно найти по их известным частным решениям. Приведем теорему о структуре общего решения линейного однородного уравнения.

Теорема (о структуре общего решения линейного однородного уравнения).

Если y₁, y₂, … , y_n – линейно независимые частные решения уравнения

,

то есть общее решение этого уравнения ( – произвольные постоянные)

Функции называются линейно независимыми в промежутке (a; b), если они не связаны никаким тождеством

,

где – какие-нибудь постоянные, не равные нулю одновременно. Для случая двух функций это условие можно сформулировать так: две функции y₁(x) и y₂(x) линейно независимы, если их отношение не является постоянной величиной: .

Например:

1) y₁=x, y₂=x² – линейно независимы;

2) , – линейно независимы;

3) , – линейно зависимы.

Достаточным условием линейной независимости n функций, непрерывных вместе со своими производными до (n – 1)-го порядка в промежутке (a; b), является то, что определитель Вронского (вронскиан) W[y₁, y₂, … , y_n] этих функций не равен нулю ни в одной точке промежутка (a; b), т.е.

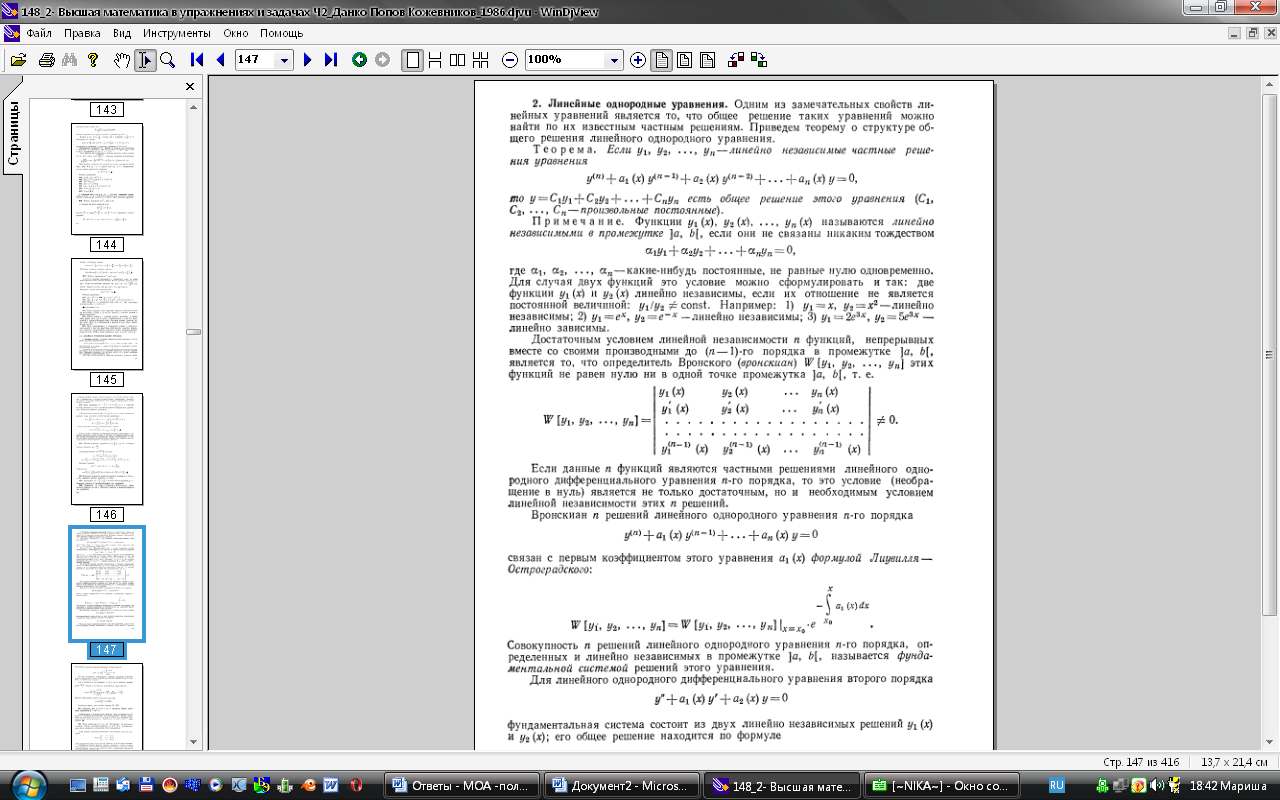
Если данные n функций являются частными решениями линейного однородного дифференциального уравнения n-го порядка, то условие необращения в нуль является не только достаточным, но и необходимым условием линейной независимости этих n решений.

Совокупность n решений линейного однородного уравнения n-го порядка, определенных и линейно независимых в промежутке (a; b), называется фундаментальной системой решений этого уравнения.

Для линейного однородного дифференциального уравнения второго порядка

фундаментальная система состоит из двух линейно независимых решений y₁(x) и y₂(x); его общее решение находится по формуле

.

Вопрос 9. Линейные однородные дифференциальные уравнения с постоянными коэффициентами.

Линейным однородным уравнением n-го порядка с постоянными коэффициентами называется уравнение вида

, (1)

где коэффициенты – некоторые действительные числа. Для нахождения частных решений уравнения (1) составляют характеристическое уравнение

, (2)

которое получается из уравнения (1) заменой в нем производных искомой функции соответствующими степенями k, причем сама функция заменяется единицей. Уравнение (2) является уравнением n-й степени и имеет n корней (действительных или комплексных, среди которых могут быть и равные).

Тогда общее решение дифференциального уравнения (1) строится в зависимости от характера корней уравнения (2):

1. каждому действительному простому корню k в общем решении соответствует слагаемое вида ;

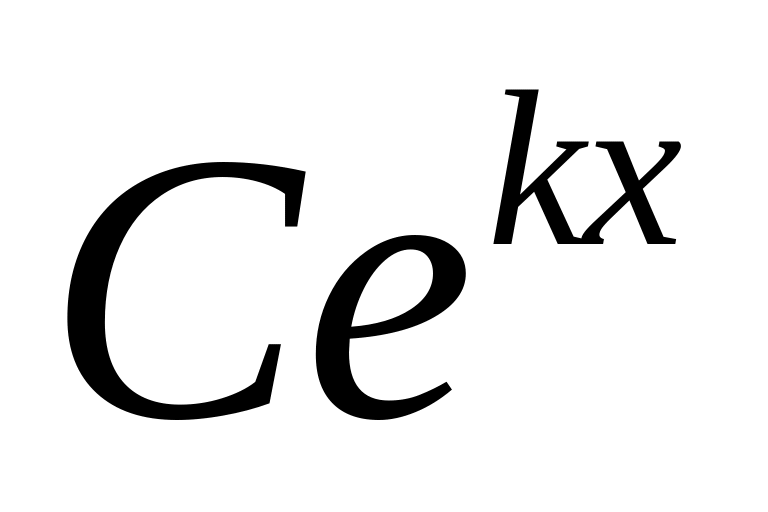2. каждому действительному корню кратности m в общем решении соответствует слагаемое вида ;

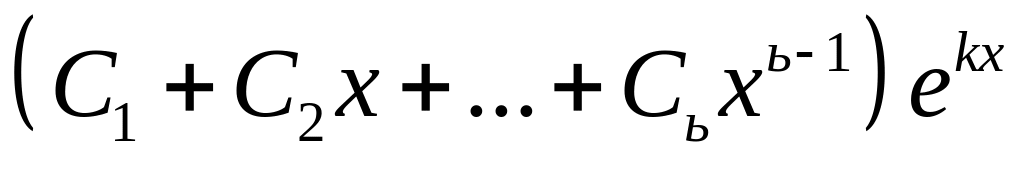3. каждой паре комплексных сопряженных простых корней k⁽¹⁾ = α + βi и k⁽²⁾ = α – βi в общем решении соответствует слагаемое вида ;

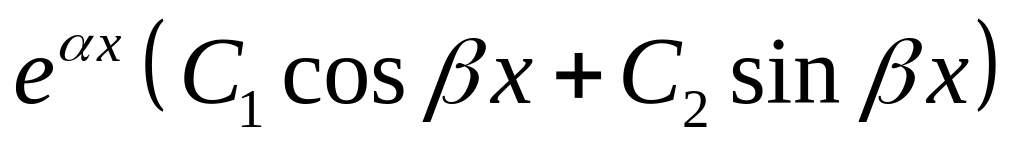4. каждой паре комплексных сопряженных простых корней k⁽¹⁾ = α + βi и k⁽²⁾ = α – βi кратности m в общем решении соответствует слагаемое вида .