6. Абстрактная алгебра

28. Множества (включая числовые N, Z, R,Q). Операции над ними.

Декардовым проижведением множества А на множество В называют множество, где 1 элемент является множеством А, 2- множеством В. Пусть множество А – произвольное множество бинарной операции на множестве В является отображение (А*А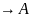 ). Для того, чтобы определить операцию необходимо определить правило по которому х,у ставился бы в соответствие один элемент z .

28. Алгебраические операции.

Способы задания операций : описательный, аналитический, графический, табличный. Алгебраические операции :

1.Комутативная (х*у=у*х)

2.Ассоциативная ((х*у)*z=х*(у*z))

3.Дистрибутивная ()

4.Сложение и умножение (аддитивная, мультиприкативная)

28. Алгебраические структуры с одной операцией: Группы.

Множество А, на котором определена одна, или несколько операций называют алгебраической структурой. Группой называются множества А, на котором определенна одна внутренняя бинарная алг-ая операция, которая подчиняется трем законам:

1.закон ассоциативности((х*у)*z=х*(у*z))

2.существование нейтрального элемента (х*е=е*х=х)

3.существование симметричного элемента ( = *х=е)

4.закон коммутативности ( х*у=у*х)

28. Алгебраические системы с двумя операциями: Кольца, Поля.

Множество А, на котором определена одна, или несколько операций называют алгебраической структурой. Кольца – алг-ая структура, если относительно + множество А является абалевой группой и выполняются законы ассоциативности и оба закона дистрибутивност, относительно +. Поля – алгебраическая структурас двумя операциями + и *, такая что относительно +множество А является абалевой группой, а относительно *множество является коммутативной группой и * дистрибутивно относительно +

28. Алгебраические системы с внутренней и внешней операциями: Векторные (линейные) пространства.

Векторные пространства – множества А с олгебраическими операциями А*А

.

28. Оператор, его матрица. Ядро, образ оператора.

Оператором называется правило по которому эл-та х из некоторого пространства Х ставится в соответствующее у из пространства У. Множество векторов у линейного пространства У для каждого из которых существует вектор х линейного пространства Х, такой, что У=Ах, называется образом оператора. Матрицей линейного оператора в базисах называется матрицей А, столбцами которой являются координаты образов базисных векторов в базисе Множества эл-ов х векторного пространства Х, которые опертор А образует в пространства У называется ядром оператора.