14.3. Недоліки квантової моделі періодичної системи елементів

Крім розглянутої дуже наближеної моделі періодичної системи елементів, яка заснована на одноелектронному наближенні, існують і інші більш складні моделі [8]. Наприклад, моделі, у яких замість усередненого потенціалу використовується ефективний потенціал , що враховує також «відцентровий внесок», або використовує потенціал Томаса-Ферм, і тощо. Проте й ці більш складні моделі також не позбавлені недоліків:

• в існуючій теорії періодичної системи використовуються стани окремих електронів електронних оболонок, а не стани електронних оболонок у цілому, що є досить грубим наближенням;

• електрон на оболонці характеризується орбітальним квантовим числом . Це припускає збереження орбітального моменту кількості руху для кожного електрону. Проте, закон збереження кількості руху справедливий лише для частинок, що рухаються в центральносиметричному силовому полі, і не має місця в інших випадках. Проте, поле складного атома, що створюється атомним ядром і електронами, не має точної сферичної симетрії. До рівняння Шредінґера повинна входити не усереднена потенціальна енергія точкового заряду, а потенціальна енергія, котра є функцією всіх координат електронів атома.

14.4. Прикінцеві зауваження

Існуючі уявлення про будову атома дозволяють, використовуючи принцип Паулі та принцип мінімізації енергії, визначити електронну конфігурацію атомів. Повністю заповненим оболонкам відповідають нульові орбітальний і спіновий моменти, внаслідок чого їх можна не враховувати при визначенні термів для валентних електронів. Вони також відіграють незначну роль при визначенні хімічних і інших властивостей елементів.

Починаючи з 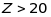, починає відігравати більш значну роль відцентрова енергія, урахування якої дозволяє в першому наближенні пояснити деталі електронної конфігурації всіх елементів періодичної системи Д.І. Менделєєва. Усе це дозволяє дійти до висновку, що періодичний закон властивостей елементів відображає періодичність у заповненні електронних оболонок атомів. Подібність властивостей елементів зв’язана з однаковою кількістю електронів на зовнішній валентній оболонці їхніх атомів.

Кількісна теорія атома потребує подальшого вдосконалення моделі, у якій необхідно більш точно врахувати особливості просторового розподілу потенціалу важких атомів.

Глава 15. Рентгенівські промені

15.1. Характеристичний спектр рентгенівських променів

Збільшення різниці потенціалів, що прискорює електрони, до значень більших за критичне , призводить до появи на тлі суцільного спектра окремих монохроматичних ліній рентгенівських променів. Ці монохроматичні лінії називаються лініями характеристичного спектра рентгенівських променів. Характеристичний спектр рентгенівських променів схематично наведено на рис. 15.1.б для декількох потенціалів на антикатоді, що прискорюють електрони: ; та схема їх досліджень

Рис. 15.1. Схема отримання характеристичних рентгенівських променів (а) та їх спектр при різних напругах на антикатоді: (б).

Експериментально встановлено такі властивості:

1. кожній речовині антикатода притаманний характеристичний спектр рентгенівських променів, який залежить від атомів, що входять до її складу;

2. характеристичний спектр складається з окремих спектральних ліній, які можна розбити на серії, що отримали назви К -, L -, М - серій відповідно. Лінії К- і L- серій мають найкоротші довжини хвиль. У елементів з з’являються лінії тільки К-серії й лише при спостерігаються лінії М- серій з більшими довжинами хвиль. Кількість ліній значно менша ніж в оптичному діапазоні.

3. 

   Рис. 15.2. К – серія для речовин з Z=37-42.

   кожна речовина має декілька критичних потенціалів , кількість яких збільшується при збільшенні атомного номера речовини антикатода;

4. при виникає лише одна найбільш довгохвильова серія характеристичних ліній спектра, при - дві серії і т.д.;

5. інтенсивність ліній характеристичного спектра зростає зі збільшенням напруги прискорення за степеневим законом де – розмірний коефіцієнт, а

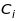6. характеристичний спектр відносно простий та одноманітний (рис.15.1 та 15.2). Спектральні лінії однієї й тієї серії зсуваються в бік менших зі зростанням , згідно закону Мозелі (рис.15.4), , де та - стала екранування атомного ядра. Для К- серії, наприклад, , а для L-серії ;

7. довжини хвиль ліній характеристичного спектра рентгенівських променів не залежать від того, чи виготовлений антикатод із простої речовини з , чи зі сплаву або сполуки;

8. ліній -серії дублетні, лінії всіх останніх серій мають складну мультиплетну структуру і поділяються на підсерії: - на три, - на п’ять, - на сім підсерій.

Усі ці властивості дозволяють дійти до висновку, що характеристичний спектр рентгенівських променів виникає при збудженні електронів глибоких оболонок атома, будова яких однакова в атомах із різними атомними номерами і не змінюється при хімічних реакціях і утворенні сплавів. Збудження рентгенівських променів можна розбити на дві стадії.

На першій стадії збудження рентгенівських променів електрони або інші елементарні частинки передають свою енергію електронам, що знаходяться на -, -, -, ....атомних шарах, внаслідок чого на них утворюються вакансії (дірки) (рис.15.3). Це означає, що чим складніший атом (чим більше його , тим більше в ньому заповнених електронами шарів, і тим більше він має критичних потенціалів 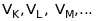– потенціалів збудження вакансій.

Рис. 15.3. Схема збудження К лінії: 1 – електрон збуджує вакансію, 2- вилітає електрон, 3- вакансія в К-шарі заповнюється електроном із L- шару з емісією кванта h.

Другою стадією утворення характеристичних спектрів рентгенівських променів є перехід електронів атома з периферичних електронних оболонок на вакансію глибинної електронної оболонки -, -, - ....атомних шарів (рис.15.3) із випромінюванням квантів електромагнітних хвиль, що формують відповідні спектральні лінії -, -, - серій характеристичного рентгенівського спектра. При цьому електрон, що переходить із периферичної оболонки на вакансію глибинного шару, рухається в кулонівському полі екранованого ядра з Згідно закону Пуассона, електричне поле в даній точці створюють лише ті заряди, які знаходяться у внутрішній частині об’єму, на поверхні якого розташована ця точка. Тому на електрон, що переходить із периферичної оболонки на глибинну з вакансією (діркою), діє електричне поле заряду, локалізованого між ядром та електронною оболонкою, на яку переходить електрон. Наприклад, якщо розглядати вакансію на К-шарі, то ефективний заряд ядра буде визначатись 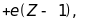бо на К-шарі є ще один електрон, що екранує ядро. Тому в полі цього екранованого ядра з 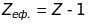буде спостерігатись одноелектронний перехід. Цей перехід майже еквівалентний електронному переходу в одноелектронному атомі з , для якого можна використовувати узагальнену формулу Бальмера.

Рис. 15.4. Залежність довжин хвиль ліній 3-х серій від атомного номера.

(15.1)

і тому виконується закон Мозлі (рис.15.4).

Величина називається сталою екранування. Вона слабко залежить від атомного номера у межах однієї серії. В таблиці 15.1 наведені значення для К - і L – серій.

Таблиця 15.1. Значення у (15.1) для К- і L - ліній.
Лінія
	1	1	2
	1	1	3
	7,5	2	3

Видно, що величина збільшується для спектральних серій зі збільшенням головного квантового числа . Більш точні вимірювання показали, що закон Мозлі наближений, бо спостерігаються відхилення від лінійної залежності але для К - і L – серій відхилення від лінійної залежності незначні.

Розглянемо тепер схему енергетичних рівнів для рентгенівських переходів. На перший погляд здається, що енергетичний рівень шару з електронною вакансією повинен бути дуже широким, бо 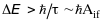, де – коефіцієнт спонтанного випромінювання Ейнштейна пропорційний . Але, згідно (12.6) і (12.14), він залежить ще й від квадрата матричного елементу потенціалу електронної взаємодії , який внаслідок відносно слабкої електронної взаємодії дуже малий. Тому - середній час перебування атома у збудженому стані (середній час життя вакансії) досить значний, що обмежує розширення енергетичного рівня. Таким чином, стан атома з вакансією на глибокому шарі можна наближено розглядати як дискретний рівень «квазістаціонарного» стану, який називається рентгенівським термом [6]. Назви рентгенівських термів збігаються з назвою шару, на якому утворюється вакансія.

На відміну від оптичної системи термів, у рентгенівському діапазоні прийнято будувати обернену систему термів, тобто терм К-шару має найбільшу енергію (рис.15.5). Причина цього лежить в різниці механізму виникнення оптичних і рентгенівських спектрів. Оптичні спектри виникають при збудженні валентного електрона зі стану з найбільшою енергію зв’язку та найменшим головним квантовим числом до стану з меншим значенням енергії зв'язку і більшим квантовим числом. Тому на енергетичній діаграмі для оптичних спектрів терми вказуються знизу вверх зі збільшенням головного квантового числа, враховуючи, що енергія зв’язку має від’ємне значення. У випадку рентгенівських спектрів збудження атома виникає внаслідок звільнення електрона з того чи іншого шару. Перехід електрона, наприклад, з L- шару до K- шару супроводжується випромінюванням фотона – кванта рентгенівських променів, енергія якого дорівнює різниці енергії зв'язку на K- і L- шарі. Оскільки енергія зв’язку електрона в К- шарі більше чим на L- шарі, тому терм К- шару малюється вище ніж терм L- шару.

На рис.15.5 наведена схема рентгенівських термів і переходи між ними. Розглянемо, як будується схема рентгенівських термів. Якщо після збудження К-шару і утворення вакансії на ньому залишається один електрон, то цей стан атома має електронну конфігурацію … Цей стан відповідає терму . При іонізації L-шару і утворенні на ньому вакансії можливі такі електронні конфігурації: . Згідно векторної моделі атома таким електронним конфігураціям відповідають наступні терми: При іонізації М-шара і утворенні на ньому вакансії можливі такі електронні конфігурації: ; . Згідно векторної моделі атома цим електронним конфігураціям відповідають наступні терми: 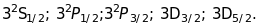Як видно з рис. 15.5, К-терм синглетний, L-терм потрійний ( L_I, L_II, L_III), M-терм складається з 5 термів (М_I, M_II, M_III, M_IV, M_V), N-терм із 7 термів. Мультиплетність рентгенівських термів впливає на відповідну мультиплетність критичних потенціалів, які також матимуть “тонку структуру”, а також на мультиплетність спектральних ліній.

Для того, щоб отримати рентгенівські спектральні серії, необхідно використати правила відбору при дипольних переходах

.

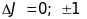. (15.2)

Ми бачимо, що, хоча через спін-орбітальну та електростатичну взаємодії мультиплетність рентгенівських термів подібна до мультиплетності квазіодноелектронного атома, але спектральні рентгенівські лінії внаслідок правил відбору мають більш складну структуру: K-серії дублетні, L- серія складається з 7 компонент і розбивається на окремі підсерії. L_I і L_II - підсерії дублетні, а лінії L_III - підсерії триплетні.

Рис. 15.5. Схема рентгенівських термів і переходів між ними.