13.5. Інтенсивність спектральних ліній

Рис.13.3. Схема 3-х енергетичних рівнів.

Інтенсивністю спектральної лінії називається величина, пропорційна потужності випромінювання одиниці об’єму речовини, що випромінює електромагнітні хвилі цих частот (або довжин хвиль). При цьому повинно бути відсутнє самопоглинання та розсіяння світла в межах об’єму зразка, що випромінює. Нехтуючи вимушеними переходами, запишемо:

(13.27)

де ,

а , і .

Розглянемо дві спектральні лінії, що утворюються при переходах із одного енергетичного рівня (Е₃) на два нижче розташованих рівні ( і ) (рис.13.3). Така ситуація має місце, наприклад, при випромінюванні дублета різкої серії лужних металів. Інтенсивність випромінювання прямо пропорційна кількості збуджених атомів і енергії кванта, що випромінюється

_,

тоді відношення інтенсивності ліній можна записати у вигляді

. (13.28)

Скориставшись формулами (13.23), (13.24) і (13.33), отримаємо

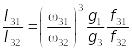(13.29)

де - сили осцилятора, які показують наскільки властивості реальних осциляторів відрізняються від переходів між стаціонарними рівнями гармонічного осцилятора, статистичні ваги нижніх рівнів.

Розглянемо конкретний випадок дублетів різкої серії натрію .(рис 13.3) З літературних даних відомо ,що ; Відношення статистичних ваг для ціх рівнів дорівнює

Відношення частот .

Тоді остаточно з формули (13.29 ) отримаємо : , що дійсно підтверджується експериментально.

13.6. Ширина спектральних ліній

Рис.13.4. Контур спектральної лінії – залежність її інтенсивності від частоти.

У раніше розглянутих розв’язках рівняння Шредінґера, наприклад, для атома водню, ми отримували енергії стаціонарних станів, котрі визначались набором точно визначених квантових чисел. Це означало, що енергетичні рівні стаціонарних атомних станів не мають ширини. Отже, спонтанні електронні переходи між ними повинні утворювати дуже вузькі спектральні лінії типу дельта-функцій від частоти. Однак, досліди показують, що реальні спектральні лінії значно ширші. Їх контур ( )) – залежність інтенсивності випромінювання від частоти відрізняється від -функції. Він значно ширший і має скінчену „напівширину”, яка визначається інтервалом частот (або ), на якому висота контуру досягає значення половини максимальної його висоти (рис.13.4). Напівширина  характеризує ступінь немонохроматичності спектральної лінії. Її визначають в одиницях кругової частоти - частоти – довжини хвилі – або хвильового числа –

Неузгодженість розрахунку з експериментом означає, що в теоретичній його моделі були використані спрощення. Дійсно, розглядалось, що атом випромінює світло з частотою , що відповідає квантовим переходам між стаціонарними рівнями і , у яких електрон може знаходитись нескінчено довго. Але спонтанний перехід порушує стаціонарність, бо необхідно враховувати радіаційне затухання – передачу енергії внаслідок взаємодії зарядженої частинки, наприклад, електрона з власним випромінюванням, поле якого створює силу Лоренца, що діє на осцилюючий електрон. Енергетичні рівні стають квазістаціонарними, бо на них електрон перебуває скінчений час , який називають часом життя електрона на цьому рівні. Точніше середнім часом життя у квазістаціонарному стані називають час , на протязі якого ймовірність перебування системи в ньому зменшується у разів.

Згідно квантової фізики радіаційне затухання, яке притаманне всім системам, що випромінюють, виникає внаслідок взаємодії атомної системи з нульовими коливаннями електромагнітного поля. Розгляд механізму цієї взаємодії виходить за межі курсу атомної фізики і розглядається у спеціальних розділах квантової механіки. Ми підійдемо по іншому до розгляду радіаційного затухання. Спочатку нагадаємо, що будь-який осцилятор спонтанно випромінює затухаючі хвилі (див. підрозділ 13.3), тобто він випромінює скінчений у часі „цуг” електромагнітних хвиль. Скінчений „цуг” хвиль не може бути монохроматичним. Він може бути представлений хвильовим пакетом, котрий складається із набору монохроматичних хвиль з різними частотами. Приклад хвильового пакету з плоских хвиль де Бройля розглядався у розділі 6.2, де було показано, що частотний інтервал пакету хвиль і час життя зв’язані співвідношенням (6.16): або . Воно вказує, що зменшення часу життя супроводжується відповідним розширенням квазістаціонарного енергетичного рівня на величину й викличе відповідне збільшення інтервалу частот , що випромінюються.

Крім радіаційного затухання коливальна система має й інші канали дисипації енергії, які викликають затухання коливань й розширення контуру спектральних ліній. Випромінювання також залежить від швидкості руху його джерела, що також впливає на . Отже, розширення контуру спектральних ліній ізольованої квантової системи залежить від таких явищ у випромінюючій системі: (1) - квантового розширення енергетичних рівнів, між якими відбуваються спонтанні переходи, (2) - ефекту Допплера, (3) - взаємодії збуджених атомів з сусідніми атомами тощо.

Класичне радіаційне затухання. Розглянемо контур спектральної лінії, яку випромінює класичний гармонічний осцилятор з частотою і коефіцієнтом затухання коливань . Згідно формули (13.18) зменшення енергії осцилятора за час визначається за формулою , яке після інтегрування має вигляд Оскільки , то амплітуда його коливань рівна:

. (13.30)

Амплітуду затухаючих коливань запишемо у вигляді інтеграла Фур’є від гармонічних коливань з різними частотами

, (13.31)

де .

Нехай осцилятор починає коливатись в момент часу , тоді

} при (13.32)

Після підстановки (13.32) у формулу для амплітуди (13.31), отримаємо

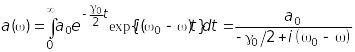. (13. 33)

Із (13.36) знайдемо відношення

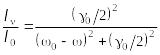. (13.34)

Вираз (13.34) описує контур спектральної лінії гармонічного осцилятора, який називається контуром Лоренца. Його напівширина знаходиться із умови :

. (13.35)

Вона визначається коефіцієнтом затухання , який характеризує дисипацію енергії коливальної системи й обернено пропорційний середньому часу життя:

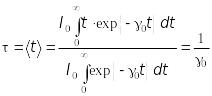. (13.36)

Отже, цей розгляд показав, що будь-які процеси дисипації енергії коливальної системи призводять до затухання її коливань або середнього часу життя системи у квазістаціонарному стані, тобто завжди має місце нерівність:

. (13.37)

Використовуючи формулу (13.19) можна оцінити коефіцієнт затухання або ширину контура спектральної лінії гармонічного осцилятора

. (13.38)

Величина  називається природною шириною (напівшириною) спектральної лінії в класичній електродинаміці (або природною шириною лінії класичного осцилятора із зарядом і масою ). Підстановка та електрона дає . Для видимого світла з або см. Експериментальні ширини ліній класичних джерел більші за ті, яку дає формула (13.38).

Квантове розширення енергетичних рівнів. Квантовий формалізм включає затухання випромінювання так повно, як і класична теорія. Інтенсивність спонтанних переходів описується коефіцієнтом Ейнштейна – ймовірністю спонтанних переходів (13.6) і (13.16), яка визначається матричними елементами оператора збурення. За допомогою запишемо зменшення кількості збуджених станів у дворівневій системі:

(13.39)

Рівняння легко інтегрується

. (13.40)

де, як і в (13.36), обернено пропорційно - середньому часу життя електрона у збудженому стані

. (13.42)

Згадаємо, що згідно співвідношення невизначеності Гейзенберга

, (13.43)

де - середній час життя атома у збудженому стані. Комбінуючи (13.42) і (13.43), отримаємо:

. (13.44)

Отже, чим більше коефіцієнт спонтанного переходу Ейнштейна , тим менше час життя електрона в збудженому стані, і тим більша ширина спектральних рівнів й тим більша напівширина контуру спектральної лінії. Скориставшись ,що отримаємо:

, (13.45)

- cила осцилятора. При спонтанних переходах, дозволених правилами відбору, електрони на рівнях мають середній час життя   10^-8 - 10^-10 с, а на метастабільних, переходи з яких заборонені, -   10^-6 - 10^-4 c.

Якщо перехід відбувається між двома збудженими станами наприклад, то природна ширина контуру спектральної лінії визначається розширенням як верхнього, так і нижнього рівнів:

, (13.46)

якщо не враховувати безвипромінювальні переходи.

Рис.13.5. Схема спостереженя впливу ефекта Доплера.

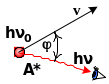
Вплив ефекту Доплера. Збуджені атоми А* це рухливі джерела світла, бо вони рухаються у просторі з тепловими швидкостями v. Згідно ефекту Доплера спостерігач сприймає світло від рухливих джерел зі зсунутою частотою , зсув якої залежить від величини і напрямку швидкості джерела світла та кута  між напрямком руху джерела світла та напрямком спостереження.

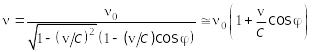, якщо (13.47) де v - швидкість збуджених атомів, а  - кут між напрямком спостереження та швидкістю, як це показано на рис.12.6.

Якщо джерелом світла є атоми з ізотропним просторовим розподілом векторів швидкості , то ефект Доплера призводить до симетричного розширення спектральної лінії. Таке розширення називається доплерівським розширенням спектральної лінії.

У випадку хаотичного теплового руху атомів та молекул імовірність того, що частинка має швидкість в інтервалі від до , дорівнює (згідно розподілу Максвелла)

, (13.48)

де – універсальна газова стала, – температура, – молярна маса, – швидкість атома чи молекули в напрямку осі , яка збігається з напрямом руху від джерела до приладу.

Використаємо формулу (13.47) за умови, що , і визначимо величини та :

(13.49)

Отже, . (13.50)

Після підстановки виразів для та в (13.48), знайдемо, що

. (13.51)

Інтенсивність випромінювання в інтервалі частот звичайно буде пропорційна до кількості частинок з такою складовою їх швидкості , що частота їх випромінювання приходиться якраз на цей інтервал частот. Але кількість таких частинок буде також пропорційна (13.51). Таким чином, розподіл інтенсивності в спектральній лінії, розширеної внаслідок повздовжнього ефекту Доплера, визначається виразом

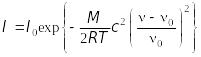, (13.52)

Звідки випливає, що спектральна лінія має гаусівську форму.

Визначимо ширину лінії з умови :

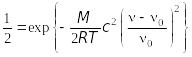
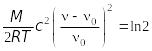. (13.53)

Звідки

. (13.54)

Отже ширина доплерівського контуру спектральної лінії буде рівна

. (13.55)

Або, враховуючи, що , одержимо

. (13.56)

Отже ефект Доплера значно розширює контур спектральної лінії. Допплерівське розширення спектральних ліній знайшло практичне застосування для експериментального вимірювання швидкості атомів і молекул в газах, плазмі газового розряду, для вимірювання швидкості руху об’єктів, що випромінюють, наприклад, в астрофізиці та радіолокації.

Вплив взаємодії збуджених атомів і молекул з іншими частинками. Взаємодія збуджених атомів і молекул з іншими частинками також змінює ширину спектральних ліній. Цей механізм, який отримав назву ударного розширення спектральних ліній, найбільш суттєво діє в оптичній області спектра при великих тисках газів, коли суттєво збільшується взаємодія випромінюючого атома іншими частинками.

Тепер розрахуємо ударну ширину спектральної лінії. Згідно теорії, ударна або статистична теорія розширення спектральних ліній дає вираз для інтенсивності спектральної лінії [4]:

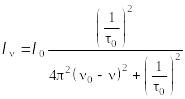, (13.57)

де – час вільного пробігу атома між двома зіткненнями. Формула для інтенсивності , аналогічна виразу для затухаючого осцилятора, якщо замінити на коефіцієнт затухання . За допомогою формули (13.57) знайдемо ширину спектральної лінії на рівні половини максимальної інтенсивності:

. (13.58)

З цього рівняння одержуємо, що

(13.59)

і, отже,

. (13.60)

З кінетичної теорії газів відомо, що , де – середня швидкість, – середня довжина вільного пробігу, – ефективний переріз розсіяння, – газокінетичний радіус атома, – концентрація атомів при температурі та тиску , – стала Больцмана. Підставивши , і у формулу (13.60) для , одержимо:

. (13.61)

Отже, загальна ширина спектральної лінії рівна

(13.62)

Розрахуємо тепер ширину спектральної лінії в довжинах хвиль. Як відомо,

(13.63)

і, отже,

, , (13.64)

де визнається з формул (13.61), (13.56), (13.45).

При малих тисках у розріджених газах найбільше впливає на ширину спектральних ліній ефект Допплера. Якщо його не враховувати, то ширина спектральних ліній визначається, головним чином, середнім часом життя збуджених електронів у атомах.

Експериментальне спостереження й вимірювання середнього часу життя збуджених електронів. Наявність затухання можна якісно спостерігати за допомогою просторового затухання випромінювання, що має місце у каналових променях при їх розповсюдженні у вакуумі. Вимірювання середнього часу життя  є більш складною задачею. Для його вимірювання використовують імпульсні джерела світла та приймачі, що можуть вмикатись через деякий проміжок часу після вимикання джерела світла. Типова схема установки для таких вимірювань наведена на рис.13.6.

Рис. 13.6. Схема установки для вимірювання середнього часу життя атома у збудженому стані: – джерело світла, i – комірки Керра ( -поляризатори), – детектор фотонів , - камера зі збудженими парами натрію.

Світловий потік квантів модулюється при проходженні крізь комірку Керра , що вмикається на короткий проміжок часу імпульсами напруги . Утворюється цуг світлових імпульсів. Світлові імпульси квантів розповсюджуються крізь пари речовини, що досліджується, наприклад, пари , і збуджує атоми цієї речовини. Збуджені атоми, наприклад , знаходяться в збудженому стані короткий час, який у середньому дорівнює . Спонтанне випромінювання квантів збудженими атомами Na* проходить крізь другу комірку Керра _, і, коли вона відкрита, то реєструється детектором. Коли друга комірка Керра за допомогою спеціальної схеми відкривається пізніше на величину то детектор не зареєструє світлового сигналу, бо оптичний сигнал за цей проміжок часу затухне. Це дозволяє досить точно вимірювати . Експериментальні значення середнього часу життя визначаються всіма процесами дисипації енергії.