11.7. Приклади застосування векторної моделі атома

Наведемо приклади застосування векторної моделі атома з нормальним (рассел-саундеровським) звязком.

(1) Атом водню Н. Атом водню ми вже розглядали з використанням векторної моделі. Його сумарне спінове число , тому терми дублетні. Лінії серії Лаймана також дублетні, а лінії серії Бальмера більш складні. Головна лінія складається із 5 ліній у видимій області спектра і однієї лінії в радіо діапазоні.

(2) Атом гелію He з має два електрона зі спіновими квантовими числами і . Сумарне спінове число має значення , тобто . Отже, гелій має дві системи термів: для ; - синглети, а для ; - триплети. Спочатку вважали, що гелій складається з двох типів атомів. Частина атомів Не з антипаралельними спінами, що мають синглетні терми, отримала назву парагелію, а друга їх частина з паралельними спінами, що мають триплетні терми, називається ортогелієм. Це звичайно не так, тому що дві системи термів характерні для одного атома, але історично збереглася термінологія для позначення системи термів (парагелій, ортогелій).

Розглянемо електронну конфігурацію і терми атому гелію. Врахуємо, що за принципом Паулі в стані можуть знаходитись два електрони лише з антипаралельними спінами, і тому для основної конфігурації існує тільки синглетний терм. Нехай один електрон завжди залишається в стані , а другий знаходиться у різних станах. Для конфігурації , можуть існувати стани з паралельними та антипаралельними спінами, тобто будуть синглетні та триплетні терми. У таблиці 11.5 наведені терми для парагелію та ортогелію На рис.11.2 приведена схема термів для гелію. Звернемо увагу, що порядок рівнів для гелію є оберненим, тобто рівні з більшим внутрішнім числом лежать нижче. Це пояснюється теоретично, якщо врахувати спін-орбітальну і спін-спінову взаємодію двох електронів між собою.

Таблиця 11.5. Терми пара- і ортогелію
парагелій					Ортогелій
 синглети					 триплети
терм			конфігурація		Терм			конфігурація
	L	J	1-й	2-й		L	J	1-й	2-й
1S0	0	0	1s1	1s1		-	-	1s1	-
1S0	0	0		2s2	3S1	0	1		1s1
1P1	1	1		2p1	3P2,1,0	1	2,1,0		2p1
1S0	0			3s1	3S1	0	1		3s1
1P1	1			3p1	3P2,1,0	1	2,1,0		3p1
1D2	2			3d1	3D3,2,1	2	3,2,1		3d1
1S0	0			4s1	3S1	0	1		4s1
1F3	3			4f1	3F4,3,2	3	4,3,2		4f1

Правила відбору для дипольних переходів дозволяють знайти спектральні серії атома Не, які наведні на рис.11.2 і в таблиці 11.6.

Синглетні лінії (головна серія) лежать в далекій ультрафіолетовій області спектра (500-600 А), синглетні спектральні лінії різкої серії - в видимому та ближньому УФ діапазоні. Синглетні спектральні лінії дифузної та фундаментальної серій в видимому та інфрачервоному областях спектра. Серії триплетних ліній – в ІЧ, УФ, та видимому діапазонах. Триплетна структура ліній дуже вузька, і для дослідження цієї структури необхідні прилади досить високої дисперсії та роздільної здатності. Перша лінія триплетної серії була знайдена в спектрі протуберанців Сонця в 1868р, що привело до відкриття гелію.

Рис.11.2. Схема термів атома гелію.

Таблиця 11.6. Квантові переходи та серії атома гелію
Парагелій	Ортогелій
* = 11S0 - n1P1	Головна серія (principal) *1 = 23S1 - n3P0 *2 = 23S1 - n3P1 * n-3 *3 = 23S1 - n3P2 триплети
* = 21P1 - n1S0	Різка (sharp) друга побічна серія *1 = 23P0 - n3S1 *2 = 23P1 - n3S1 *f(n) *3 = 23P1 - n3S1 триплети
* =21P1 - n1D2	Дифузна(diffusion)перша побічна серія *1 = 23P0 - n3D1 *12f(n) *2 = 23P1 - n3D1 *23f(n) *3 = 23P1 - n3D2 *4 = 23P2 - n3D1 секстети *5 = 23P2 - n3D2 *6 = 23P2 - n3D3
* = 31D2 - n1F3	Фундаментальна (fundamental) серія *1 = 33D1 - n3F2 *12f(n) *2 = 33D2 - n3F2 *23 n-3 *3 = 33D2 - n3F3 *34 n-3 *4 = 33D3 - n3F2 *45 n-3 *5 = 33D3 - n3F3 *6 = 33D3 - n3F4 секстети

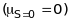Парагелій не має в незбудженому стані магнітного моменту , а ортогелій має 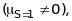тому атом гелію – діамагнітний в стані парагелію, а в стані ортогелію - парамагнітний.

Атом гелію має також метастабільні рівні та переходи з яких на основний рівень ¹S₀ заборонені правилами відбору 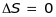. Експериментально встановлено, що метастабільні стани Не мають досить великі енергії та великий час життя.

Ці дані використовувуються на практиці.

Наприклад, якщо електрони розсіюються на збуджених до метастабільного стану атомах гелію Не*, то вони передають свою енергію збудження електрону, що розсіюється. Розсіяний електрон збільшує кінетичну енергію, що може бути зареєстровано. Зіткнення, при яких потенціальна енергія збудження перетворюється в кінетичну, називаються зіткненнями другого роду.

. (11.15)

На практиці для зменшення напруги запалювання електричного розряду в газах як корисну домішку до робочого "тіла” гелій- неонового лазера використовують атоми Не*,збуджених на метастабільний рівень

(3) Пара- і орто- позитроній. Позитроній може мати сумарне спінове число при антипаралельних спінах електрона і позитрона і при паралельних спінах електрона і позитрона. Тому позитроній має два стани пара- і орто- з або з . Парапозитроній має синглетні терми і синглетні лінії. Він не має магнітного моменту в не збудженому стані і тому він діамагнітний. Ортопозитроній має триплетні терми і магнітний момент, що не дорівнює нулю.

(4) Літій Li має електронну конфігурацію . Сумарне спінове число . Його терми дублетні: ; ; ; ; _, тощо. Схема подібних термів на прикладі атомів натрію вже розглядалась раніше (глава 9).

(5) Берилій Be 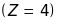має електронну конфігурацію в незбудженому стані 1s²2s². У випадку коли спіни антипаралельні , і основним термом атома берилію є . Для збуджених електронних конфігурацій атом берилію може мати синглетні терми:

У другому випадку коли збуджений атом берилію має сумарне спінове число , будемо мати триплетні терми:

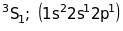
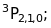
Детально енергетичні стани берилію представлені в таблиці 11.7.

Таблиця 11.7. Енергетичні стани берилію
Електронна конфігурація	Синглетні	Триплетні
1s22s2 (2p0)  	1S0
1s22s12p1   	1P1
  		3P03P13P2
1s22s1(2p0)3s1   	1S0	3S1
1s22s1(2p03s0)3p1   	1P1
  		3P03P13P2
1s22s1(…3s03p0)3d1   	1D2
  		3D13D23D3
1s22s1 (... 3d 0)3f1   	1F3
  		3 F23F33F4

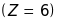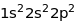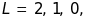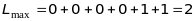(6) Вуглець C має електронну конфігурацію в незбудженому стані . Значення квантового числа сумарного орбітального моменту кількості руху бо і 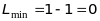. У залежності від електронної конфігурації С може мати стани з різними сумарними спіновими числами, як наведено в таблиці 11.8. (дивись задачу №5, розділ 9 [1].

Таблиця 11.8. Енергетичні стани вуглецю
Електронна конфігурація	Триплетні терми	Синглетні терми
1s22s22p2
  	3P0; 3P1; 3P2
  		1S0; 1D2
1s22s22p13s1
   	3P0; 3P1; 3P2
   		1P1
1s22s2(2p13s0)3p1   	3P0; 3P1; 3P2;3S1; 3D1; 3D2;3D3
  		1S0; 1P1; 1D2
1s22s2 (2p3p0)3d1   	3P0; 3P1; 3P2; 3D1;3D2;3D3; 3F2;3F3;3F4
  		1P1; 1D2 ;1F3

(7) Фтор F. . Електронна конфігурація у не збудженому стані . Видно, що необхідно перейти до розгляду еквівалентного електрона в стані У цьому разі 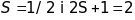. Отже терми фтору дублетні: .

11.8. J-J зв’язок

зв’язок менш поширений ніж (нормальний) зв’язок. Він застосовується для класифікації термів важких атомів (з великими Z). Енергія взаємодії орбітальних і спінових моментів у випадку зв’язку менша за енергію спін-орбітальної взаємодії

(11.16)

Рис. 11.3. зв’язок: а) - ,

б) - , в) - .

Тому в цій моделі спочатку знаходять сумарний вектор спінового та орбітального моментів кількості руху для кожного електрона атома

, (11.17)

а потім знаходять сумарний вектор повного моменту кількості руху всіх електронів.

, (11.18)

де - нове квантове число, яке визначає абсолютну величину сумарного моменту кількості руху. Воно може бути знайдене за допомогою співвідношення

, (11.19)

де останній член суми повинен бути найменшим значенням по модулю при комбінації чисел . Символічний запис терма при зв'язку .

Кількість можливих значень квантового числа не залежить від типу зв’язку. Це твердження виникає внаслідок, так званого, принципу адіабатичної інваріантності. У випадку та зв’язків можна пересвідчитись, що максимальні значення числа для них збігаються.

Дійсно, для зв’язку, а для 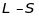зв’язку .

Розглянемо приклад sp- стану, коли

(а) Спочатку знайдемо квантові числа для 1-го і 2-го електронів:

1) - для першого електрону , тому що

2) для другого електрону , тому що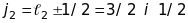

(б) Потім знайдемо значення квантових чисел , які визначаються нерівністю

для двох станів: одного при і другого при

Для першого стану .

Для другого стану .

Рис.11.4 Схема термів стану для і зв’язків, з якої видно, що кількість станів не залежить від типу звязку.

Таким чином, утворилося 4 окремих стани з різними квантовими числами: . Їх кількість така, як і у випадку нормального зв’язку, для якого в стані сумарне спінове число має два значення - 0 і 1, а орбітальне , тобто утворюється чотири терма для нормального типу зв’язку

Вони наведені на рис.11.4 ліворуч: один синглетний рівень – і три триплетних Більш глибокими будуть триплетні стани з паралельними спінами.

У середній частині рис.11.4 наведено чотири терма, що попарно групуються і . Із них терми - синглетні, бо число 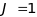можна отримати, коли спіни антипаралельні Дійсно , коли , а терми - триплетні, бо коли , можна отримати і 2 . Дозволені переходи між окремими термами визначаються правилами відбору для квантових чисел:

.

Кількість термів, як вже вказувалося, не залежить від вибору моделі, тому спочатку у нульовому наближенні використовують для систематики термів нормальний зв’язок, а потім при розгляді важких елементів переходять до використання зв'язку. Вибір моделі змінює правило інтервалів, інтенсивності ліній та їх поведінку у зовнішніх полях. У випадку зв’язку рівні з меншими розташовані глибше рівнів з більшими , тоді як у випадку зв'язку це правило порушується, як це видно на рис.11.4.