20.8. Ефект Холла

Безпосередній експериментальний доказ існування квазічастинок із від'ємною ефективною масою - дірок (або квазічастинок із позитивною ефективною масою, але додатнім зарядом) дає ефект Холла⁴⁴. В ефекті Холла вимірюється різниця потенціалів , що виникає в провіднику зі струмом у перпендикулярному до напрямку проходження струму магнітному полі . На рис 20.13 зображена схема для

Рис. 20.14. Схема вимірювання ефекту Холла (а), дія магнітного поля на дірки (б) та на електрони (в).

вимірювання ефекту Холла. Нехай струм густиною , що тече вздовж осі провідника, утворюється рухом позитивних зарядів (рис.20.11.б). Сила Лоренца , що виникає під дією магнітного поля у речовині відхиляє позитивні заряди до нижньої поверхні зразка. Виникає електричне поле , що називається полем Холла, яке в рівноважних умовах компенсує дію сили Лоренца (відхиляючий вплив магнітного поля)

, (20.34)

або

, (20.35)

де - струм, 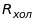- опір Холла, - розмір провідника в напрямку вздовж магнітного поля, а d - товщина зразка. Отже, з (20.35) бачимо: знак напруги Холла визначається за даними умовами досліду знаком носіїв струму, а величина опору Холла дозволяє визначити концентрацію цих носів. Досліди показали, що є такі речовини, у яких струм створюють дірки (позитивні заряди). Якщо в проходженні струму беруть участь одночасно електрони та дірки, то ефект Холла стає більш складним, і може навіть дорівнювати нулеві за умови, що

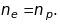
20.9. Електропровідність металів

Рис.20.15. Рух квазічастинок.

Під дією електричного поля в металі протікає електричний струм. У його утворенні беруть участь електрони провідності. Вони прискорюються електричним полем і переходять на вакантні місця, звільнюючи при цьому свої попередні місця для нових вакансій, які заповнюються іншими електронами й так далі. В ідеальному кристалі з абсолютною періодичною ґраткою при нульовій абсолютній температурі електрони не розсіюються, тобто вони мають нескінченну довжину вільного пробігу. Їхня функція Блоха буде біжучою хвилею, модульованою з періодом, що збігається з періодом кристалічної ґратки. Вона розповсюджується в кристалі без затухання. Досліди показали, що в бездомішкових кристалах металів при К опір прямує до нуля.

У реальних кристалах електричне поле прискорює електрони лише протягом середнього часу їхнього життя між двома послідовними актами розсіяння . Після великої кількості актів прискорення та розсіяння встановлюється середній імпульс або середня дрейфова швидкість у напрямку електричного поля , що прискорює

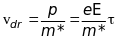, (20.36)

де - елементарний заряд, - ефективна маса квазічастинки.

Дрейфова швидкість визначає густину електричного струму , що протікає в провіднику під дією електричного поля

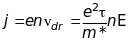, (20.37)

тобто має місце закон Ома 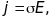де - питома електропровідність. Вона залежить від дрейфової швидкості в одиничному полі , яку прийнято називати рухливістю квазічастинок, та - концентрації вільних, здатних рухатися квазічастинок (електронів) у не заповненій або частково заповненій зоні

, (20.38)

де рухливість

(20.39)

визначається процесами розсіяння та зонною структурою . Оцінка за допомогою (20.39) швидкості електронів у полі дає , тобто квазічастинка – електрон дуже повільно, як „черепаха”, дрейфує в металі. Аналіз формул (20.38) показує, що концентрація електронів у металах слабко залежить від температури, і тому температурна залежність електропровідності визначається, головним чином, температурної зміною рухливості. Рухливість залежить від процесів розсіяння електронів, які змінюються зі зміною температури. Дійсно, у вираз для рухливості (20.39) входить час релаксації , зв’язаний з довжиною вільного пробігу та середньою швидкістю носіїв заряду . У металі електронний газ вироджений, тому в знаменнику стоїть , де - швидкість носіїв із енергією Фермі. При високих температурах розсіяння носіїв відбувається, головним чином, на фононах – квазічастинках, які зіставляються з хвилями зміщення атомів (іонів) ґратки із рівноважних положень⁴⁵. Рух атомів у кришталевій ґратці в нормальних координатах можна звести до коливань гармонічного осцилятора, енергія кожного з яких має дискретні значення 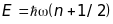, де - частота нормальних коливань. Отже, моди коливань можуть змінюватись лише порціями , які називаються фононами. Енергія коливань кристала приблизно дорівнює сумі енергій фононів, бо не прийнято включати енергію нульових коливань ґратки . Залежність кількості теплових фононів з енергією від температури (Т) визначається формулою Планка . Довжина вільного пробігу 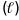, від якої залежить час релаксації , пропорційна концентрації фононів при . 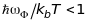Тому .

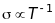Електропровідність часто зв’язують із площею ізоенергетичної поверхні Фермі, яка для сферичної поверхні Фермі дорівнює:

, (20.40)

де і – імпульс і енергія Фермі відповідно.

Згідно формули (20.28), концентрація електронів залежить від енергії Фермі:

. (20.41)

Після підстановки цього виразу для у формулу для із урахуванням (20.41) отримаємо

. (20.42)

Формула (20.42) показує, що перенесення електронів у металах здійснюється квазічастинками - електронами, що знаходяться на ізоенергетичній поверхні Фермі. Вона була доведена у випадку сферичної поверхні Фермі, але виявляється, що вона має такий самий вигляд і в інших випадках, коли враховувати динаміку електронів провідності в металах із несферичними поверхнями Фермі. Тому поняття поверхні Фермі досить часто використовується в сучасній теорії металів.

Відзначимо, що електропровідність твердих тіл є проявом квантово-механічних властивостей квазічастинок. Дійсно, розглянемо електропровідність одновимірного провідника, яка згідно закону Ома дорівнює:

, (20.43)

де та - струм та падіння напруги в одновимірному провіднику. Струм визначається проходженням заряду е крізь його поперечний переріз за одиницю часу, тоді

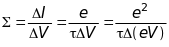. (20.44)

Якщо вважати, що є час між двома станами розсіяння квазічастинки, а 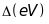є невизначеність її енергії, то згідно співвідношення невизначеності , і тому електропровідність буде дорівнювати:

. (20.45)

Отже електропровідність є проявом квантовомеханічних властивостей заряджених частинок, що підтверджується сучасними експериментами, а називається квантовою одиницею електропровідності.