§ 7. Производная функции, ее свойства и приложения

7.1. Определение производной функции в точке

Определение 7.1.

Пусть функция y=f(x) определена в некоторой окрестности точки x0. Производной f′(x0) функции y=f(x) в точке x0 называется предел отношения приращения функции Δy к приращению аргумента Δx в этой точке при стремлении приращения аргумента к нулю, если этот предел существует и конечен, т.е.

f′(x0)=limΔx→0ΔyΔx=limΔx→0f(x0+Δx)−f(x0)Δx,                                       (7.1)

где Δx=x−x0.

Часто производную функции y=f(x) в точке x0 обозначают y′x(x0), y′(x0) или yx(x0) .

Операция нахождения производной функции называется дифференцированием функции.

Пример 7.1.

Используя определение 7.1, найти производную функции y(x)=x3 в точке x0=−1.

Р е ш е н и е.

 Запишем приращение функции:

Δy=f(−1+Δx)−f(−1)=(−1+Δx)3−(−1)3=−1+3Δx−3(Δx)2+(Δx)3+1==Δx(3−3Δx+(Δx)2)

Тогда ΔyΔx=3−3Δx+(Δx)2 и y′(x0)=limΔx→0ΔyΔx=limΔx→0(3−3Δx+(Δx)2)=3.

Предел (7.1) в точке x0 может не существовать или быть бесконечным. В этом случае функция f(x) не имеет производной в точке x0. Если предел (7.1) равен ∞, −∞ или +∞, то говорят, что функция f(x)имеет бесконечную производную в точке x0.

Пример 7.2.

Используя определение 7.1, найти производную функции y=x√ в точках: 1) x0=1; 2) x0=0.

Р е ш е н и е.

 Найдем предел в формуле (7.1) для каждого случая: 1) limΔx→0f(x0+Δx)−f(x0)Δx=limΔx→01+Δx√−1Δx=limΔx→0(1+Δx)−1Δx(1+Δx√+1)=limΔx→011+Δx√+1=12  2) limΔx→0f(x0+Δx)−f(x0)Δx=limΔx→00+Δx√−0Δx=limΔx→01Δx√=∞. Следовательно, функция y=x√ в точке x0=1 имеет конечную производную y′(1)=12, в точке x0=0 - бесконечную производную.

Пример 7.3.

Показать, что функция f(x)=|x| не имеет производной в точке x0=0.

Р е ш е н и е.

 Учитывая, что |x|={  x,  x≥0;−x, x<0, вычислимlimΔx→0f(x0+Δx)−f(x0)Δx=limΔx→0∣∣Δx∣∣−0Δx={  1,  Δx>0  (x→+0),−1,  Δx<0  (x→−0). Пределы справа ислева в точке x0=0 существуют, конечны, но не равны между собой и поэтому предела (7.1) в точке x0=0 не существует. Следовательно, функция f(x)=|x| не имеет производной в этой точке (рис. 7.1) .

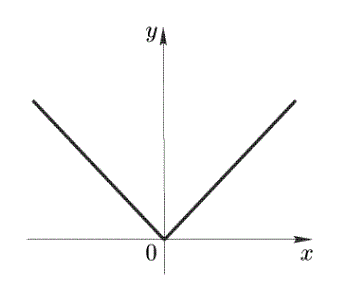
Рис. 7.1

Пусть функция f(x)определена на некотором отрезке [a, b]. Тогда за ее производную в точке x0=a или в точке x0=b принимают соответственно предел справа или предел слева отношения f(x0+Δx)−f(x0)Δx при x→x0 (см. определения 3.24, 3.25). Эти пределы называют соответственно правой или левой производнойфункции f(x) в точке x=a или в точке x=b.

Отметим, что если функция y=f(x) определена на некотором промежутке и f′(x) существует в каждой точке этого промежутка, то формула

f′(x)=limΔx→0f(x+Δx)−f(x)Δx

определяет производную f′(x) как функцию аргумента x. В дальнейшем при дифференцировании функции y=f(x), если не указана точка, будем находить производную при всех допустимых значениях аргумента x и записывать ее в виде y′(x) или y′.

Пример 7.4.

Найти производную постоянной функции y=c.

Р е ш е н и е.

 Очевидно, что Δy=c−c=0 ΔyΔx=0∀x∈R. Согласно формуле (7.1) имеем y′(x)=limΔx→0ΔyΔx=0. Следовательно, c′=0.

Пример 7.5.

Найти производную функции y=sinx.

Р е ш е н и е.

 Используя формулу для разности синусов двух углов и учитывая, что sinΔx2~Δx2 при x→0 (см. табл. 5.1), находим

y′(x)=limΔx→0ΔyΔx=limΔx→0sin(x+Δx)−sinxΔx=limΔx→02⋅sinΔx2⋅cos(x+Δx2)Δx==limΔx→02⋅Δx2⋅cos(x+Δx2)Δx=limΔx→0cos(x+Δx2)=cosx.

Следовательно, (sinx)′=cosx.

Пример 7.6.

Продифференцировать функцию y=ax (a>0,  a≠1).

Р е ш е н и е.

 Запишем Δy=f(x+Δx)−f(x)=ax+Δx−ax=ax(aΔx−1). Учитывая, что aΔx−1~Δx⋅lna при Δx→0 (см. табл. 5.1), получим

y′=limΔx→0ΔyΔx=limΔx→0ax(aΔx−1)Δx=ax⋅limΔx→0Δx⋅lnaΔx=ax⋅lna.

Следовательно, (ax)′=ax⋅lna. В частности, (ex)′=ex.