2.4 Реконструкция дифференциальных уравнений системы методом Магницкого.

В ряде случаев, в том числе и в проблеме управления хаосом, необходимо решать задачу восстановления системы дифференциальных уравнений исходя из заданного множества точек в фазовом пространстве, принадлежащих аттрактору системы.

Множество точек, определяющее отрезок траектории нерегулярного аттрактора в пространстве , задает некоторую кривую, которая может быть описана, например, параметрически , — множество значений независимой переменной (или количество точек в заданном множестве). Предположим также, что случайные погрешности, с которыми заданы точки множества, некоррелированны и имеют нулевое математическое ожидание. Множество 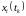фактически определяет значения 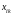сеточных функций, заданных на сетке . Последние задают в фазовом пространстве некоторую сеточную траекторию . Аппроксимируем множество значении , сеточной функции в фазовом пространстве решением 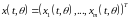системы дифференциальных уравнений

(2.4.1)

на промежутке с начальным условием 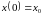, где

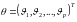— вектор параметров, — размерность пространства параметров. Из множества решений системы (1.10.1) необходимо выбрать такое , траектория которого в фазовом пространстве наиболее близка к заданной сеточной функции . Для оценки близости используем функционал

(2.4.2)

Задача состоит в том, чтобы найти такое значение вектора параметров , при котором функционал (1.10.2) будет иметь наименьшее значение. Необходимое условие экстремума функционала

,

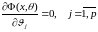равносильно системе из уравнений

, (2.4.3)

нелинейных относительно неизвестного вектора параметров .

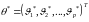Для численного решения системы (1.10.3) с помощью итерационного процесса разложим решение в ряд Тейлора в некоторой точке

(2.4.4)

и отбросим величины второго порядка малости. Тогда, подставляя

(1.10.4) в (1.10.3), получим систему алгебраических уравнений 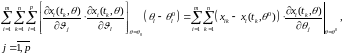линейную относительно приращений . В векторной форме

последняя система имеет вид

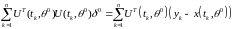, (2.4.5)

где 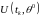матрица с элементами

Матрица является решением дифференциального матричного линейного неоднородного уравнения с начальным 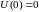, где

Таким образом, все необходимые составляющие для решения системы (1.10.5) линейных алгебраических уравнений находятся из решения следующей системы дифференциальных уравнений

(2.4.6)

на отрезке при указанных выше начальных условиях. Матрицы и в (1.10.1) вычисляются при значении вектора 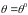и

Найденное при решении системы (1.10.5) значение 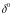минимизирует сумму квадратов

и является в фазовом -мерном пространстве оценкой наименьших квадратов для вектора . Поэтому величина 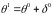будет являться уточненной по отношению к оценкой вектора параметров и далее может использоваться для последующего улучшения решения, если в приведенном выше алгоритме вместо значения положить . Таким образом, начиная с некоторого значения найдем последовательность векторов ,

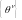
где — номер итерации. Предел этой последовательности при

есть решение задачи.