Реконструкция динамических систем методом задержки Система Магницкого
Н.А.Магницким была предложена система трех нелинейных дифференциальных уравнений, описывающих изменение макропоказателей рыночной экономики:
Примем
интервал времени
.
Зафиксируем
значение параметра δ=0.6546. Проинтегрируем
данную систему методом Рунге-Кутта 4-го
порядка. В результате численного
интегрирования получим трехмерный
временной ряд. Зададим параметры
реконструкции
,
.
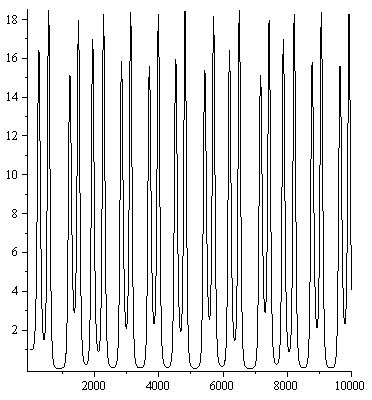
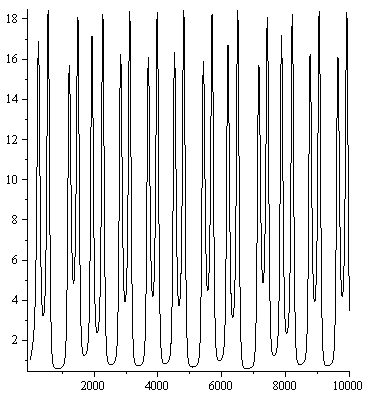
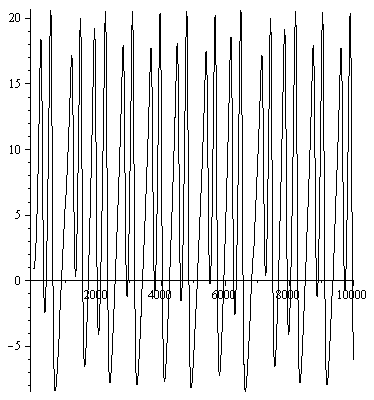
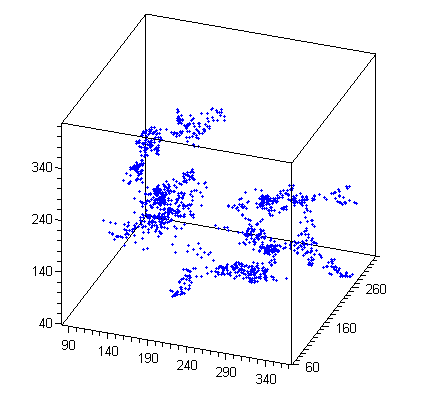
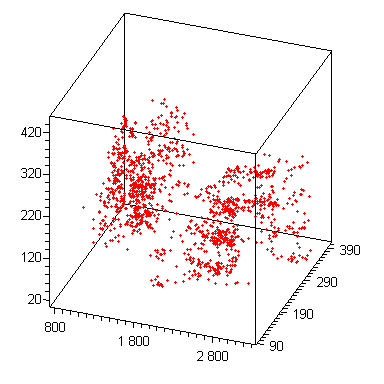
Рис . Временные ряды численного решения системы Магницкого
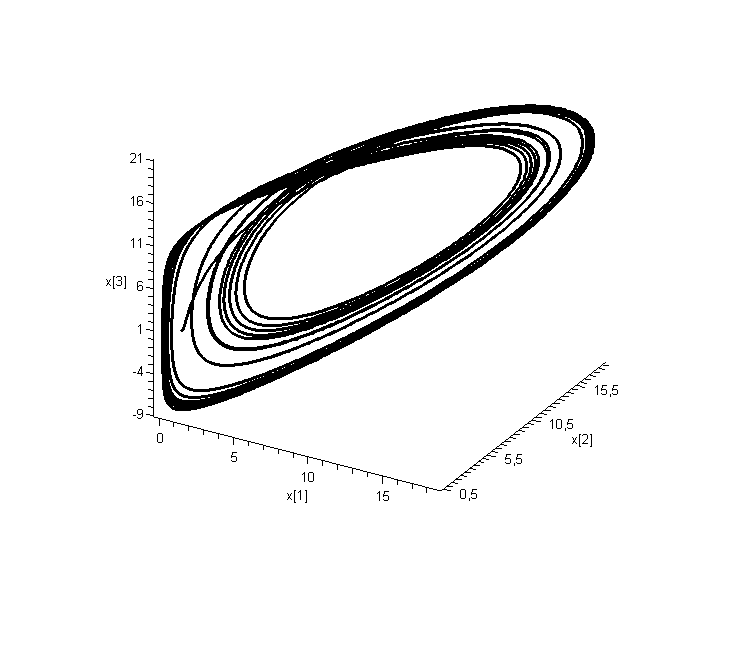
Рис . Аттрактор исходной системы Рис . Реконструкция по переменной х[1]
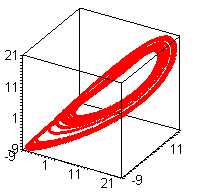
Рис . Реконструкция по переменной х[2] Рис . Реконструкция по переменной х[3]
Реконструкция динамических систем методом отображения
Произведём восстановление динамической системы в виде отображений на примере временного ряда цен на сырьё (1300 значений).
Табл. 2.3.1 Значения цен на сырьё
Газпром |
Норникель |
Аэрофлот |
218.89 |
2318.13 |
45.15 |
224 |
2338.2 |
45.31 |
228.38 |
2383 |
44.68 |
224.47 |
2456.01 |
44.2 |
228.75 |
2534.89 |
44.41 |
По
алгоритму, описанному в теоритической
части, получаем значение вектора
неизвестных параметров
в виде:
С= |
-202448.71 |
-6147.76 |
392.21 |
19286.20 |
0.86 |
80.29 |
-13.71 |
-1613700.92 |
-50857.06 |
3332.04 |
15138.38 |
6.66 |
691.05 |
-112.98 |
|
-21209.87 |
-671.71 |
44.00 |
1995.56 |
0.09 |
9.13 |
-1.49 |
Далее пробегаем циклом по всем i:
изобразим результат в виде аттрактора:
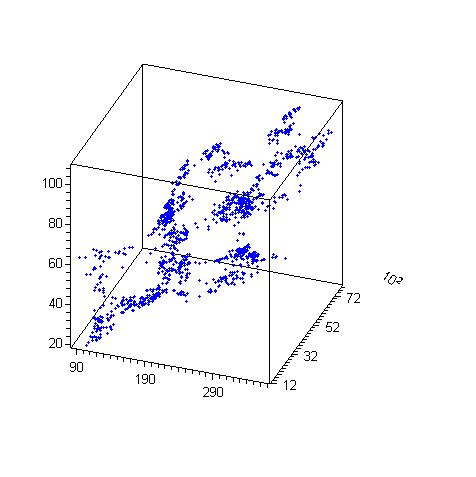
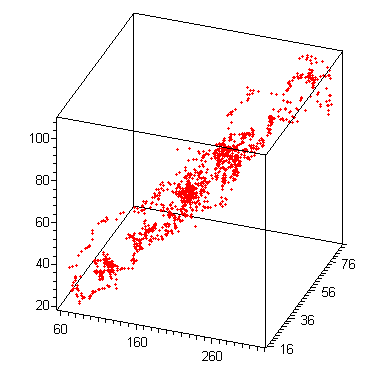
Рис , Аттрактор исходной системы Рис , Реконструированный аттрактор
Табл. 2.3.1 Значения цен на сырьё
Лукойл |
МТС |
Роснефть |
2145 |
196 |
203.95 |
2161.5 |
195.99 |
203.26 |
2180.2 |
192.52 |
202 |
2170.31 |
193.05 |
201.99 |
2241 |
192.87 |
202.69 |
По алгоритму, описанному в теоритической части, получаем значение вектора неизвестных параметров в виде:
С= |
74540.86 |
-111.44 |
94.12 |
-8552.63 |
-0.43 |
28.62 |
0.44 |
691896.90 |
-611.72 |
850.80 |
-80340.99 |
-4.07 |
260.94 |
4.84 |
|
9068.08 |
-11.86 |
11.41 |
-1047.51 |
-0.05 |
3.49 |
0.06 |
Далее пробегаем циклом по всем i:
изобразим результат в виде аттрактора:
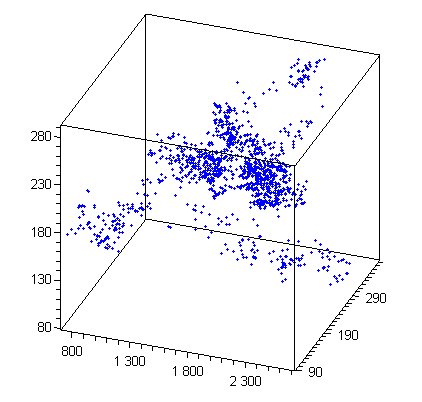
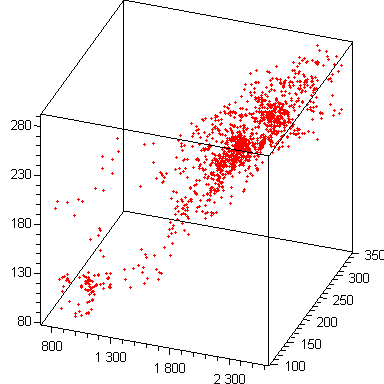
Табл. 2.3.1 Значения цен на сырьё
Газпром |
РБК |
Новатэк |
218.89 |
63.86 |
127.11 |
224 |
66.11 |
130 |
228.38 |
66.1 |
131.5 |
224.47 |
65 |
135 |
228.75 |
65.55 |
137.5 |
По алгоритму, описанному в теоритической части, получаем значение вектора неизвестных параметров в виде:
С= |
-260.84 |
233.66 |
-17.95 |
-178.90 |
-0.01 |
-4.20 |
0.44 |
-18385.97 |
2665.14 |
-213.37 |
-827.87 |
-0.07 |
-50.75 |
4.85 |
|
-178.20 |
30.79 |
-2.44 |
-12.43 |
0.00 |
-0.57 |
0.06 |
Далее пробегаем циклом по всем i:
изобразим результат в виде аттрактора:
