Уравнения состояния реальных газов

Хотя модель идеального газа хорошо описывает поведение реальных газов при низких давлениях и высоких температурах, в более экстремальных условиях её согласие с опытом гораздо хуже. В частности, это проявляется в том, что реальные газы могут быть переведены в жидкое и даже в твердое состояние, а идеальные — не могут. Для более точного описания поведения реальных газов при низких температурах была создана модель газа Ван-дер-Ваальса, вводящая поправку на конечный диаметр молекулы и на притяжение молекул на больших расстояниях (напомним, что в идеальных газах частицы считаются точечными и никак не взаимодействуют на расстоянии). Термическим уравненим состояния (называется связь между давлением, объемом и температурой. Для одного моля газа Ван-дер-Ваальса оно имеет вид:

В идно, что это уравнение фактически является уравнением состояния идеального газа с двумя поправками. Поправка a учитывает притяжение молекул, поправка b — конечный объем молекулы.

Уравнение ВДВ качественно хорошо описывает свойство реальных газов паров, но не удовлетворяет практическим целям с количественной точки зрения, особенно при высоких давлениях и низких температурах. Оно легло в основу нескольких других уравнений, более точных. Уравнение Беркла, Дитеричи, Редлиха-Квонга Более точным является многопараметрическое уравнение состояния. К таким уравнениям относят уравнение Битти-Бриджи, уравнение Казавинского, уравнение Беннедикта-Вебба-Рубина, Мартини-Лод.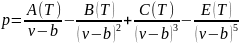 Для описания свойств воды и водяного пара особенно в области перегретого состояния 2 физиками было разработано уравнение состояния на основе теории ассоциации молекулы воды.

Уравнение Ван-дер-Ваальса и его анализ. Критическое состояние вещества

Уравнение состояния газа Ван-дер-Ваальса — уравнение, связывающее основные термодинамические величины в модели газа Ван-дер-Ваальса. Хотя модель идеального газа хорошо описывает поведение реальных газов при низких давлениях и высоких температурах, в более экстремальных условиях её согласие с опытом гораздо хуже. В частности, это проявляется в том, что реальные газы могут быть переведены в жидкое и даже в твердое состояние, а идеальные — не могут. Для более точного описания поведения реальных газов при низких температурах была создана модель газа Ван-дер-Ваальса, вводящая поправку на конечный диаметр молекулы и на притяжение молекул на больших расстояниях (напомним, что в идеальных газах частицы считаются точечными и никак не взаимодействуют на расстоянии). Термическим уравненим состояния (называется связь между давлением, объемом и температурой. Для одного моля газа Ван-дер-Ваальса оно имеет вид:

В идно, что это уравнение фактически является уравнением состояния идеального газа с двумя поправками. Поправка a учитывает притяжение молекул, поправка b — конечный объем молекулы.Для ν молей газа Ван-дер-Ваальса уравнение состояния выглядит так: Уравнение можно переписать так, чтобы выразить в явном виде давление или объем Уравнение содержит объем в третьей степени и, следовательно, имеет или три действительных корня, или один действительный и два мнимых. При высоких температурах уравнение имеет один действительный корень, и по мере повышения температуры кривые, вычисленные по уравнению Ван-дер-Ваальса, приближаются к гиперболам, соответствующим уравнению состояния идеального газа.

Принципиальное значение уравнения Ван-дер-Ваальса определяется следующими обстоятельствами:

1) уравнение было получено из модельных представлений о свойствах реальных газов и жидкостей, а не явилось результатом эмпирического подбора функции f(p,V,T), описывающей свойства реальных газов;

2) уравнение долго рассматривалось как некоторый общий вид уравнения состояния реальных газов, на основе которого было построено много других уравнений состояния

3) с помощью уравнения Ван-дер-Ваальса впервые удалось описать явление перехода газа в жидкость и проанализировать критические явления. В этом отношении уравнение Ван-дер-Ваальса имеет преимущество даже перед более точными уравнениями в вириальной форме

Критическое состояние вещества: Как известно, уравнение состояния устанавливает функциональную связь между p, V, T и числом молей n газа в состоянии равновесия. Самым простым и известным уравнением состояния является уравнение состояния идеального газа: pV = nRT. Реальные газы описываются уравнением состояния идеального газа только приближенно, и отклонения от идеального поведения становятся заметными при высоких давлениях и низких температурах, особенно когда газ близок к конденсации.

Критическое состояние –состояние вещества в точках фазовых переходов II рода. Критическое состояние, являющееся предельным случаем равновесия двухфазных систем, наблюдается в чистых веществах при равновесии жидкость — газ, а в растворах — при фазовых равновесиях газ — газ, жидкость — жидкость, жидкость — газ, твёрдое тело — твёрдое тело. На диаграммах состояния Критическое состояние соответствуют предельные точки на кривых равновесия фаз. С приближением к Критическое состояние различия в плотности, составе и др. свойствах сосуществующих фаз, а также теплота фазового перехода и межфазное поверхностное натяжение уменьшаются и в критической точке равны нулю. При приближении к Критическое состояние физические свойства вещества резко изменяются: теоретически неограниченно возрастает теплоёмкость и восприимчивость системы к внешним воздействиям (например, изотермическая сжимаемость в случае чистых жидкостей). Критическое состояние необходимо во многих областях науки и техники: при создании энергетических установок на сверхкритических параметрах, сверхпроводящих систем, установок для сжижения газов, разделения смесей и т. д.