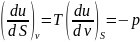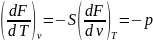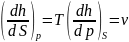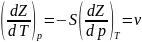- •Предмет и метод термодинамики. Термодинамика, как теоретическая основа теплоэнергетики и теплотехники
- •Основные понятия и определения термодинамики. Параметры состояния.
- •Основные законы идеальных газов. Уравнения состояния идеальных газов.
- •Газовые смеси
- •Теплоемкость газов и газовых смесей, их определение.
- •Первый закон термодинамики и его математические выражения
- •Энтропия как функция состояния и её смысл.
- •Второй закон термодинамики и его математические выражения.
- •Исследования изохорного процесса идеальных газов.
- •Исследование изобарного процесса идеальных газов.
- •Исследование адиабатного процесса идеальных газов
- •Исследования изотермического процесса идеальных газов.
- •Исследования политропного процесса идеальных газов
- •Эксергия, её свойства и физический смысл
- •Дифференциальные уравнения внутренней энергии и энтальпии
- •Дифференциальные уравнения энтропии и теплоемкости
- •Потенциальные функции
- •Уравнения состояния реальных газов
- •Уравнение Ван-дер-Ваальса и его анализ. Критическое состояние вещества
- •Пары, общие понятия и определения. Процесс парообразования.
- •Дифференциальное соотношение Клапейрона-Клаузуиса. Применение
- •Паровые процессы и их расчет Циклы пту. Общая характеристика. Цикл Ренкина и его анализ.
- •Влияния начальных и конечных параметров пара на эффективность пту
- •Цикл пту с промежуточным перегревом пара
- •Циклы теплофикационных паротурбинных установок
- •Циклы холодильных машин и тепловых насосов
- •Циклы ядерных энергетических установок
- •Циклы бинарных энергетических установок
- •Эксергия, её свойства и физический смысл
- •Циклы ядерных энергетических установок
Дифференциальные уравнения внутренней энергии и энтальпии
Внутренняя
энергия.Запишем дифференциальное
уравнение внутренней энергии в виде
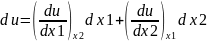 .
Выбирая в качестве независимых переменных
x1=v и x2=T
определим значения частных производных
.
Выбирая в качестве независимых переменных
x1=v и x2=T
определим значения частных производных
 .
В соответствии с отношениями
и отношением Максвелла
.
В соответствии с отношениями
и отношением Максвелла
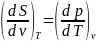 имеем
имеем
 .
Из термодинамики идеальных газов
известно, что
.
Из термодинамики идеальных газов
известно, что
 есть
истинная удельная теплоемкость при
постоянном объеме Cv.
Поэтому дифф уравнение внутренней
энергии примет вид
есть
истинная удельная теплоемкость при
постоянном объеме Cv.
Поэтому дифф уравнение внутренней
энергии примет вид
 .
Выразим связь u=u(T,p)
в дифференциальной форме
.
Выразим связь u=u(T,p)
в дифференциальной форме
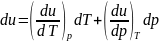 .
Обозначим T=x1
и p=x2, и
учитывая
.
Обозначим T=x1
и p=x2, и
учитывая
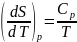 ,
получим
,
получим
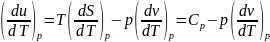 .
Производную
.
Производную
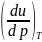 можно
представить как
можно
представить как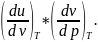 Первый множитель тут равен красному.
Отсюда (по тройному произведению, где
че-то там равно -1) получим
Первый множитель тут равен красному.
Отсюда (по тройному произведению, где
че-то там равно -1) получим
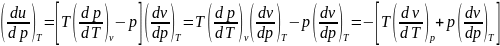 .
При подстановке синего
и зеленого в черное_жирное.
.
При подстановке синего
и зеленого в черное_жирное.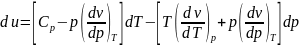
Энтальпия.
В
термодинамических расчетах широко
используется калорический параметр–
энтальпия.h=u+pv.
Если принять за независимые переменные
T и p, то
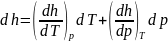 .
Из термодинамики идеальных газов
известно, что
.
Из термодинамики идеальных газов
известно, что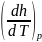 есть
Cp. Частную производную
представим в виде
есть
Cp. Частную производную
представим в виде
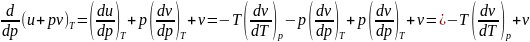 .
Подставив выражения найденных производных
во второе уравнение получим
.
Подставив выражения найденных производных
во второе уравнение получим
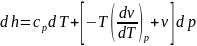 .
.
Как функция
T и v:
имеем
 ,
в окончательном виде:
,
в окончательном виде:
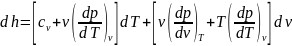
Как функция
p и v:
имеем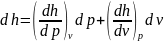 ,
окончательно получим
,
окончательно получим
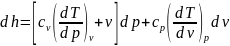
Дифференциальные уравнения энтропии и теплоемкости
Энтропия.
Получим дифференциальные соотношения
для дельной энтропии. Пусть
S=S(T,v), тогда
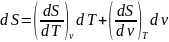 . Величину производной
. Величину производной
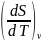 можно вычислить используя математическое
выражение второго закона термодинамики
применительно к изохорному процессу:
можно вычислить используя математическое
выражение второго закона термодинамики
применительно к изохорному процессу:
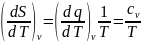 По соотношению максвелла
отсюда
По соотношению максвелла
отсюда
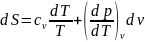 .
.
Аналогично
при независимых T и p.
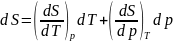 отсюда
отсюда

Аналогично
при независимых p и v:
 отсюда
отсюда
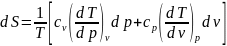 .
Сравнивая данное уравнение с математическим
выражением второго закона термодинамики
.
Сравнивая данное уравнение с математическим
выражением второго закона термодинамики
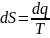 ?
приходим к одной из возможных форм
записи дифференциального уравнения
первого закона термодинамики.
?
приходим к одной из возможных форм
записи дифференциального уравнения
первого закона термодинамики.
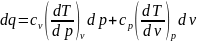
Теплоемкость.
Как известно, теплоемкость играет существенную роль при выполнении многих теплотехнических расчетов. Особо важное значение имеют Cp и Cv, входящие в дифференциальные связи для u,h и S. Зависимости Cp и Cv от температуры находят экспериментально или рассчитывают на основе квантовой теории веществ. Зависимости от p и v можно установить с помощью дифференциальных термодинамических связей.
Продифференцировав
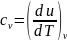 по
v:
по
v:
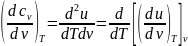 ,
используя
получим
,
используя
получим
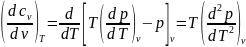 .
Проинтегрировав выражение, получим
зависимость
.
Проинтегрировав выражение, получим
зависимость
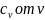 при неизменной температуре.
при неизменной температуре.
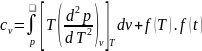 это
зависимость теплоемкости от температуры
вещества в идеально газовом состоянии.
это
зависимость теплоемкости от температуры
вещества в идеально газовом состоянии.
Для
получения зависимости от давления:
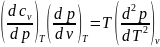 или
или .
Проинтегрируем по p.
.
Проинтегрируем по p.
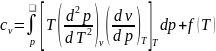
Аналогично
и для теплоемкости Cp:Продифференцируем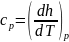 по p.
по p.
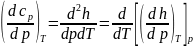 .
Подставляя вместо
.
Подставляя вместо
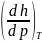 выражение
выражение
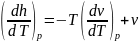 получим
получим
 после интегрирования
после интегрирования
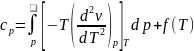 .
Если перепишем в виде
.
Если перепишем в виде
 Проинтегрировав
найдем зависимость от v
Проинтегрировав
найдем зависимость от v
 .
.
В
экспериментальных исследованиях
определение Cp проще и
надежнее, поэтому необходимо помнить
связи. -
показатель Пуассона, или показатель
адиабаты. Для газов K>1.
-
показатель Пуассона, или показатель
адиабаты. Для газов K>1.
Потенциальные функции
При термодинамических расчетах и анализе широко используются потенциальные функции. Наибольшее значение в термодинамике имеют потенциалы: внутренняя энергия, энтальпия, а также энергия Гельмгольца, или изохорно-изотермический потенциал. F=u-TS и энергия Гиббса, или изобарно-изотермический потенциал Z=h-TS. Название потенциалов эти функции получили потому, что их производные по соответствующим независимым переменным дают значения параметров состояния системы. Частные производные легко воспроизводятся с помощью мнемонического квадрата Планка.
Термодинамический потенциал |
Обозначение |
Связь с внутренней энергией |
Частные производные |
Внутренняя энергия |
u |
u |
|
Энергия Гельмгольца |
F |
u-TS |
|
Энтальпия |
h |
u+pv |
|
Энергия Гиббса |
Z |
u+pv-TS |
|