14. Типы уравнений.
Задача Коши для уравнения теплопроводности.
Найти
функцию u(t
, x)
в области
,
удовлетворяющую уравнению
и начальным данным u(0, x) = u0(x), где u0(x) — заданная функция.
Смешанная задача для уравнения теплопроводности.
Найти
функцию u(t
, x)
в области
,
удовлетворяющую уравнению
начальным данным u(0, x) = u0(x) и краевым условиям, записанным в общей форме
Смешанная задача для уравнения переноса.
Найти функцию u(t , x) в области , удовлетворяющую уравнению (для определенности положим c > 0):
начальным данным Коши
u(0, x) = u0(x), t = 0
и левому краевому условию
Смешанная задача для волнового уравнения.
Найти функцию u(t , x) в области , удовлетворяющую уравнению
с начальными данными
и
краевыми условиями
Эллиптическая краевая задача (уравнение Пуассона).
Найти
функцию u(x
, y)
в области
,
удовлетворяющую уравнению
и
краевым условиям
,
,
15. Идея метода сеток.
Простейший способ построения численных решений для уравнений в частных производных — метод сеток. В дальнейшем, наряду с методом сеток, будем рассматривать и другие подходы к численному решению задач , например, вариационные, методы конечных элементов.
Рассмотрим постановку разностной задачи в методе сеток на примере одномерного уравнения теплопроводности.
Для
решения одномерной смешанной задачи
для уравнений в частных производных
параболического типа область определения
искомой функции покрывается расчетной
сеткой с узлами в точках {tn,
xm},
n
= 0, ... , N,
m
= 0, ... , M ,
tn
= nτ,
xm
= mh,
τ
= T/N,
h
= X/M ,
где τ,
h
— шаги сетки по времени и пространству
соответственно. Приближенным решением
задачи назовем сеточную функцию
.
Верхний индекс в такой форме записи
сеточной функции традиционно указывает
на номер слоя по времени, нижний (нижние)
— на номер узла сетки по пространственной
координате (рис.
1.1).
Рассмотрим подходы к построению численных алгоритмов для приближенного решения уравнений в частных производных.
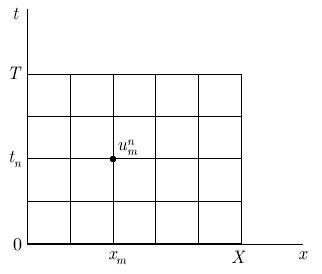
Рис. 1.1.
16. Аппроксимационные методы.
Пусть
и
—
операторные обозначения исходной
дифференциальной и аппроксимирующей
ее разностной задачи (точнее,
параметрического семейства задач);
и
—
соответственно, дифференциальный и
разностный операторы,
—
решения дифференциального и разностного
уравнений , принадлежащие соответствующим
функциональным пространствам,
—
правая часть исходного уравнения и ее
проекция на расчетную сетку. Считается
известным способ получения проекции
непрерывной функции на сетку. В простейшем
случае используются значения функции,
вычисленные в узлах сетки. Индекс τ
в этой операторной записи указывает на
всю совокупность сеточных параметров.
Можно сказать, что для дискретной задачи
имеется не один оператор, а совокупность
различных операторов , зависящих от
набора параметров.
Например, задачу Коши для линейного одномерного уравнения переноса
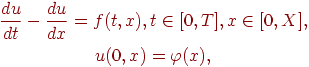
можно представить в виде
Здесь
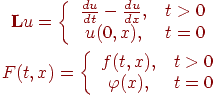
Одна из аппроксимирующих эту задачу разностных схем (правый уголок) имеет вид
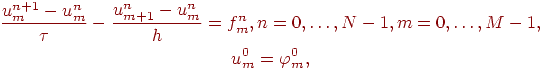
или в операторной форме
где
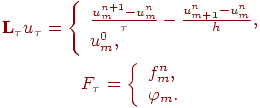
Определение
1.
Говорят, что решение uτ
сходится
к решению при
,
если
где
Uτ
— проекция точного решения на разностную
сетку; причем, если имеет место оценка
,
,
то сходимость
имеет порядок p.
В качестве примера исследуем на сходимость разностную схему для задачи Коши для обыкновенного дифференциального уравнения (схема Эйлера)
аппроксимирующую простейшее ОДУ
Из разностного уравнения
un = (1 - λτ)un - 1
найдем его общее решение:
Решение дифференциальной задачи легко находится:
u(t) = ae - λt.
Величина
погрешности решения, входящая в
определение сходимости,
тогда будет
Представим
в
виде
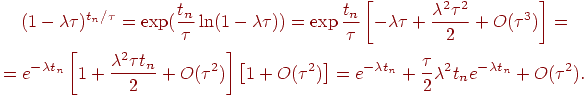
Тогда
и, следовательно,
т.е. разностная схема имеет первый порядок сходимости