40. Проблема реальности в квантовой физике

Классическая механика в микромире и для околосветных скоростей неприменима. Релятивистская физика, основанная на теории относительности, применима к скоростям, близким к скорости света, а квантовая – к миру атомов и элементарных частиц.

Рассмотрим релятивистскую формулу массы:

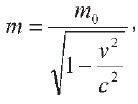
где m 0 – масса покоя тела, v – скорость его движения. При уменьшении отношения до нуля, что может быть достигнуто или при v = 0 (покой), или при c = БЕСКОНЕЧНОСТИ(идея мгновенного распространения света), масса становится величиной постоянной m = m0, как это и признавалось в классической механике до А. Эйнштейна.

Известное соотношение E=m ? c2дает для массы то же переменное значение: m = E/c2

Скорость света есть величина постоянная, но сообщаемая телу извне энергия должна сказываться на величине массы. Релятивистская формула сложения скоростей в случае движения со скоростью света (фотон, нейтрино) приводит к выводу:

т. е. два фотона, обладающих каждый скоростью с, при движении навстречу друг другу сближаются не со скоростью с2как этого требовал бы здравый смысл, а все с той же скоростью с.

Если в релятивистской физике границы применимости были связаны с огромностью и постоянством скорости света (с = 300 000 км/с), то в квантовой механике границы применения классической физики связаны с малостью постоянной Планка (h= 6,62 ? 1 0-27эрг ? с).

Волновые свойства материи, которые не рассматривает классическая физика, характеризуются длиной волны де Бройля:

Чем короче длина волны, тем больше импульс – основная характеристика материальной частицы, и, наоборот, увеличение импульса (или скорости) приводит к уменьшению длины волны, т. е. уменьшению волновых свойств. Для микромира с его частицами малой массы длина волны достигает размеров, позволяющих измерить ее и обнаружить волновую природу частиц (явление дифракции). В макромире вследствие чрезвычайной малости hдлина волны получается исчезающе-малой.

Так, если человек средней массы идет со скоростью 5 км/ч, то длина соответствующей волны получается порядка 10-23см.

Математически соотношение неопределенности можно записать так:

?р?х = h где ?р и ?х – неточности (неопределенности) в значении импульса и координаты, а h=h/2? Записав ?р = mAv можно придать соотношению неопределенности иную форму:

?v?x = x/m

Если импульс частицы известен точно, то ?х = x/Q т.е. координаты совершенно неопределенны. В классической механике, где импульс и координаты вполне определены, соотношение выглядит так: ?р?х = 0. Чем ближе мы к этому предельному случаю, тем с большим правом можно применять законы классической механики. Для дробинки массой в 1 г такая неточность в макромире неощутима.

41. Детерминизм и причинность в современной физике, динамические и статистические законы

Что общего между прыгающим по земле мячиком, лазером, планетной системой, бурлящим потоком воды в ручье, биологической популяцией? Общее в том, что все эти объекты могут рассматриваться как динамические системы. Абстрагируясь от конкретной физической природы объекта, о нем говорят как о динамической системе, если можно указать такой набор величин, называемых динамическими переменными и характеризующих состояние системы, что их значения в любой последующий момент времени получаются из исходного набора по определенному правилу. Это правило задает, как говорят, оператор эволюции системы.

Например, для прыгающего мячика оператор эволюции определяется законами движения в поле тяжести и удара мячика о поверхность. Мгновенное состояние задается двумя величинами – расстоянием от земли и скоростью. Геометрически оно изображается как точка на фазовой плоскости, где эти две величины отложены, соответственно, по оси абсцисс и ординат. Изменение состояния во времени, или, для краткости, динамика системы, отвечает движению изображающей точки по определенной кривой – фазовой траектории. Если состояние системы задается набором N величин, динамику можно представить как движение точки по траектории в N-мерном фазовом пространстве.

Выделяют два класса динамических систем – консервативные (к ним относятся, например, механические колебательные системы в отсутствие трения) и диссипативные. Для диссипативных систем характерно то, что режим динамики, возникающий в системе, предоставленной себе в течение длительного времени, становится не зависящим от начального состояния (по крайней мере при вариации начальных условий в некоторых конечных пределах). Множество точек в фазовом пространстве диссипативной системы, посещаемых в установившемся режиме, называется аттрактором. Простые примеры аттракторов – устойчивое состояние равновесия и предельный цикл, отвечающий режиму периодических автоколебаний (замкнутая фазовая траектория, на которую наматываются все близкие траектории).

Замечательным достижением теории динамических систем стало открытие хаотической динамики. Возникновение хаоса кажется на первый взгляд несовместимым с определением динамической системы, подразумевающим возможность однозначного предсказания конечного состояния по исходному. На самом деле противоречия нет. В хаотическом режиме сколь угодно малая неточность в задании начального состояния системы быстро нарастает во времени, так что предсказуемость становится недостижимой на достаточно больших интервалах времени. Такого рода режимы характеризуются нерегулярным, хаотическим изменением динамических переменных во времени. В фазовом пространстве диссипативных систем им отвечают странные аттракторы – сложно устроенные множества, демонстрирующие все более тонкую структуру на разных уровнях ее разрешения.

Первая линия развития, которая вела к представлениям о динамическом хаосе, связана с небесной механикой. Основоположниками классической механики принято считать И. Ньютона, Ж.Л. Лагранжа, П.С. Лапласа, У.Р. Гамильтона. Они сформировали представления о том, что мы сейчас называем гамильтоновой, или консервативной, динамической системой.