4 Теорема сложения и умножения вероятности.

P (A/B)- условная вероятность события A при условии , что соб.B произошло.

усл.вер-ть P(A/B) усл.вер-ть P(B/A) -теорема умножения для зависимых соб.А и В.

Если соб.А не влияет на вер-ть соб.В и наоборот,то они независимы: P(A/B)=P(A); P(B)=P(B/A) => P(AB)+P(A)*P(B) – вер-ть произ-ния соб-й равна произ-нию вер-тей.

P(ABC)=P(AH)*P(A/H)=P(BC)*P(A/BC)=P(C)*P(B/C)*P(A/BC) (ВС обозначили за Н) Опр-е независимости для А,В и С- соб. А,В и С назыв.независимыми в совокупности,если выполн.след усл-я:

Если попарно независимы P(AB)=P(A)*P(B), P(BC)=P(B)*P(C), P(AC)=P(A)*P(C).
P(ABC)=P(A)*P(B)*P(C)

P(A+B)=P(A)+P(B) вер-ть суммы двух несовместных событий

- ф-ла сложения вер-тей двух совместных событий

P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(BC)-P(AC)+P(ABC) вер-ть суммы трех несовместных соб-й. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.

5. Формула полной вероятности и формула Байеса.

Формула полной вероятности

Пусть Н₁,Н₂…Н_k подмножества пространства эл.соб-й , такие что:

H_i H_j=, i≠j и I,j=1,2,…,k
H1+H2+…+H_k= 

В этом случае говоря,что сис-ма подмножеств Н₁,Н₂…Н_kобразует разбиение множества . Для любого соб.А,являющего подмножеством , верна ф-ла полной вер-ти

P(A)= События H_iназываются гипотезами по отношению к соб.А,а вер-ти Р (H_i) трактуются как доопытные вер-ти гипотез, причем  Р (H_i)=1.

Формула Байеса Если известно, что соб.А произошло, то априорные(после опыта) вер-ти гипотез H_i,очевидно, должны быть пересчитаны, так как появилась доп.информация. Апостериорные вер-ти гипотез H_i,при условии, что соб.А произошло,вычисляются по ф-ле Байеса:

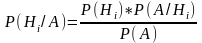,i=1,2,…,k,

где Р(А) определяется по ф-ле полной вер-ти. истор.процесса – локальная цивилизация – общность людей, объединенных дух.традициями и проживающие на одной тер-и. Выделяет первичные, вторичные и третичные цивилизации. Свыше 20 цив-ций. Сейчас основных 8 (западно-христ, православно-христ, иудейская, исламская, индуистская, дальневосточная, буддистская, конфуцианская). 4 этапа развития: генезис, рост, упадок и дезинтеграция.

Недостатки: не принимает во внимание качественные различия хозяйственных систем в современном мире.

- теория единой цивилизации

- теория столкновения цивилизаций

5.Дискретные случайные величины. Ряд распределения. Числовые характеристики.

Пусть (,F,P) – дискретное вероятностное пространство.

Числовая ф-ция Х=Х() определенная на пространстве эл.соб-й называется дискретной случ.величиной.

Сис-ма равенств: P[x=x_i]=р_i, ш=1,2…n,.. определяет распределение вероятностей дискретной слу.величины Х. Очевидно,что р_i≥0,  р_i=1

Простейшей формой закона распределения дискретной величины является ряд распределения.

X_i	x1	x2	x3	…	х_n	…
P(x=x_i)	P1	P2	P3	…	p_n	…

Графической интерпретацией ряда распределения является многоугольник распределения.

Функция распределения случайной величины.

Для непрерывных случайных величин применяют такую форму закона распределения, как функция распределения.

Функция распределения случайной величины Х называется ф-ция F(х), определяемая для любого действительного зн-я х,как вер-ть события [Х<х], т.е. F(х)=Р[Х<х].

Функция распределения обладает следующими свойствами:

0≤F(х)≤1
F(x)- неубывающая ф-ция х, если если х₂>х₁,то F(х₂)>F(х₁)

Функция может быть изображена в виде графика. Для непрерывной величины это будет кривая изменяющееся в пределах от 0 до 1, а для дискретной величины - ступенчатая фигура со скачками.

Числовые характеристики случайной величины.

Математическое ожидание случайной величины.

Пусть Х- дискретная случ.величина,принимающая зн-я х₁,х₂.. с вероятностями р₁,р₂.. Математическое ожидание M[x] случ.величины X определяется формулой