18. Тригонометрическая формула комплексного числа

Если вещественную x и мнимую y части комплексного числа выразить через модуль r = | z | и аргумент   (x = rcos φ, y = rsin φ), то всякое комплексное число z, кроме нуля, можно записать в тригонометрической форме

z = r(cos φ + isin φ).

Формула Муавра и извлечение корней из комплексных чисел

Эта формула позволяет возводить в целую степень ненулевое комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид:

zn = [r(cos φ + isin φ)]n = rn(cos nφ + isin nφ),

где r — модуль, а   — аргумент комплексного числа. В современной символике она опубликована Эйлером в 1722 году. Приведенная формуле справедлива при любом целом n, не обязательно положительном.

Аналогичная формула применима также и при вычислении корней n-ой степени из ненулевого комплексного числа:

z1 / n = [r(cos(φ + 2πk) + isin(φ + 2πk))]1 / n =

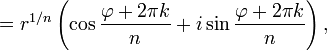
Отметим, что корни n-й степени из ненулевого комплексного числа всегда существуют, и их количество равно n. На комплексной плоскости, как видно из формулы, все эти корни являются вершинами правильного n-угольника, вписанного в окружность радиуса  с центром в начале координат 

1. Умножение. Модуль произведения равен произведению модулей, аргумент произведения равен сумме аргументов:

 

2. Деление. Модуль частного равен частному модулей, аргумент частного равен разности аргументов:

 

3. Возведение в целую степень п. Модуль возводится в эту степень, аргумент умножается на п.

  

22. Матрицы. Ранг матрицы. Теоремы.

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы, в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.

Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.

Ранг матрицы

Количество линейно независимых строк матрицы называют строчным рангом матрицы, а количество линейно независимых столбцов матрицы называют столбцовым рангомматрицы. В действительности, оба ранга совпадают. Их общее значение и называется рангом матрицы.

Другой эквивалентный данному подход заключается в определении ранга матрицы, как максимального порядка отличного от нуля минора матрицы.

• Теорема (о базисном миноре): Пусть 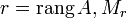  — базисный минор матрицы A, тогда:

  1. базисные строки и базисные столбцы линейно независимы;

  2. любая строка (столбец) матрицы A есть линейная комбинация базисных строк (столбцов).

• Следствия:

• Если ранг матрицы равен r, то любые p:p > r строк или столбцов этой матрицы будут линейно зависимы.

• Если A — квадратная матрица, и 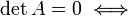 , то строки и столбцы этой матрицы линейно зависимы.

• Пусть 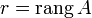 , тогда максимальное количество линейно независимых строк (столбцов) этой матрицы равно r.

Теорема (об инвариантности ранга при элементарных преобразованиях): Введём обозначение A∼B для матриц, полученных друг из друга элементарными преобразованиями. Тогда справедливо утверждение: Если A∼B, то их ранги равны.