16. Случайные величины и их виды. Мат.Ожидание. Дисперсия.
Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать. Случайные величины могут принимать дискретные, непрерывные и дискретно-непрерывные значения. Соответственно случайные величины классифицируют на дискретные, непрерывные и дискретно-непрерывные. Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретной случайной величины. Закон распределения может быть задан аналитически, в виде таблицы или графически. Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения. Графическое представление этой таблицы называется многоугольником распределения. При этом сумма все ординат многоугольника распределения представляет собой вероятность всех возможных значений случайной величины, а, следовательно, равна единице.
М
атематическим
ожиданием
называется среднее значение данной
случайной величины
Свойства математического ожидания.
а)
,
где
;
б)
;
в)
;
г)
если случайные величины
и
независимы, то
.
Дисперсией называется математическое ожидание квадрата отклонения СВ от ее математического ожидания
Дисперсия служит для характеристики рассеяния СВ относительно ее математического ожидания
Свойства дисперсии
а)
,
где
;
б)
;
в)
,
где
– ковариация двух случайных величин
и
17. Комплексные числа. Действия над ними. Геометрическая интерпретация комплексных чисел
Ко́мпле́ксные чи́сла — расширение множества вещественных чисел, обычно обозначается С. Любое комплексное число может быть представлено как формальная сумма x + iy, где x и y — вещественные числа, i — мнимая единица.Комплексные числа образуют алгебраически замкнутое поле — это означает, что многочлен степени n с комплексными коэффициентами имеет ровно n комплексных корней (основная теорема алгебры). Это одна из главных причин широкого применения комплексных чисел в математических исследованиях.
Действия над комплексными числами
Сравнение a + bi = c + di означает, что a = c и b = d (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).
Сложение (a + bi) + (c + di) = (a + c) + (b + d)i.
Вычитание(a + bi) − (c + di) = (a − c) + (b − d)i.
Умножение
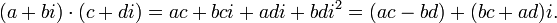
Д
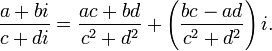еление
Геометрическая интерпретация комплексных чисел состоит в том, что каждому комплексному числу z = x + yi ставится в соответствие точка (x, y) координатной плоскости таким образом, что действительная часть комплексного числа представляет собой абсциссу, а коэффициент при мнимой части – ординату точки. Таким образом, устанавливается взаимно однозначное соответствие между множеством комплексных чисел и множеством точек координатной плоскости. Подобным образом было установлено соответствие между множеством действительных чисел и множеством точек числовой прямой.