24. Решение систем линейных уравнений в MathCad
kn1x1 + kn2x2 + … + knnxn + ln = 0
Здесь kij и li — какие-то числовые константы, называемые, соответственно, коэффициентами и свободными членами уравнений, а xj — переменные. Такие уравнения обычно записывают также с помощью матриц: KX + L = 0
Здесь K — матрица (kij), составленная из коэффициентов при переменных величинах, где i — номер строки матрицы, а j — номер столбца. X и L — это, соответственно, векторы, составленные из переменных и свободных членов. Собственно, при решении СЛУ с помощью MathCAD мы будем записывать СЛУ именно в таком виде, потому что решение СЛУ в MathCAD реализовано именно с помощью матричных методов.
Для решения СЛУ можно использовать функцию lsolve. У нее есть два параметра: первый — это матрица коэффициентов уравнений, а второй — вектор свободных членов. То есть для получения результата нам нужно написать: lsolve(K_, L_) =
Ну, а после знака равенства MathCAD нам уже нарисует результат.
25. Блочный метод решения уравнений и систем в MathCad
Для
решения системы этим методом необходимо
выполнить следующее:
a) задать начальное приближение для всех неизвестных, входящих в систему уравнений;
б) задать ключевое слово Given, которое указывает, что далее следует система уравнений;
в) ввести уравнения и неравенства в любом порядке (использовать кнопку логического равенства на панели знаков логических операций для набора знака «=» в уравнении);
г) ввести любое выражение,которое включает функцию Find.
Решающим блоком называется часть документа, расположенная междуключевыми словами Given и Find.
После набора решающего блока Mathcad возвращает точное решение уравненияили системы уравнений.
Обратиться к функции Find можно несколькими способами:
Find(x1, x2,…) = - корень или корни уравнения вычисляются и выводятся в окно документа.
x := Find(x1, x2,…) – формируется переменная или вектор, содержащий вычисленные значения корней.
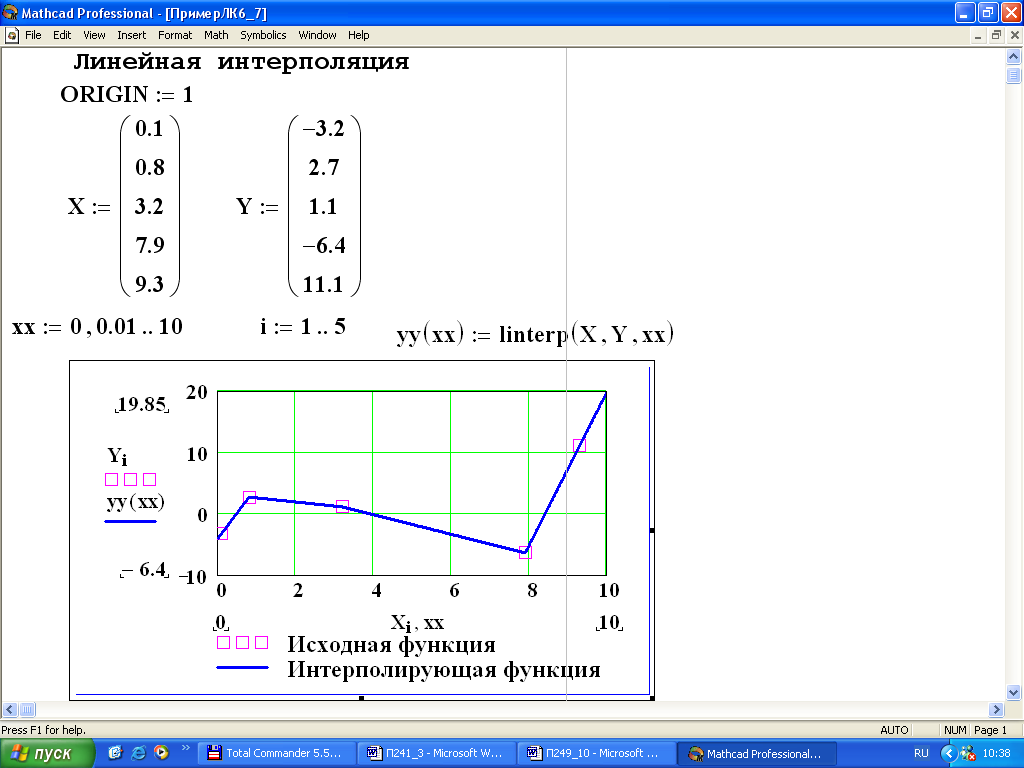
Линейная интерполяция данных в MathCad.
Линейная интерполяция осуществляется с помощью встроенной функции linterp, имеющей следующий общий вид:
linterp(VX,VY,x),
VX, VY – векторы координат узловых точек;
x – значение аргумента, для которого будет получено интерполяционное значение функции y.
27. Сплайновая интерполяция данных в MathCad
В MathCAD для проведения кубической сплайн-интерполяции предлагается три встроенные функции (VX, VY – вектора узловых точек):
cspline(VX, VY) – возвращает вектор вторых производных (VK) при приближении в опорных точках к кубическому полиному;
pspline(VX, VY) – возвращает вектор вторых производных (VK) при приближении в опорных точках к параболической кривой;
lspline(VX, VY) – возвращает вектор вторых производных (VK) при приближении в опорных точках к прямой.
Интерполирующая функция строится с помощью стандартной функции interp, имеющей следующий общий вид:
interp(VK,VX, VY,x),
VK – вектор вторых производных сплайна в опорных точках;
x – произвольная точка, в которой вычисляется значение интерполирующей функции.
Последовательность кубической сплайн-интерполяции такова:
- создаются вектора VX и VY, содержащие координаты точек, через которые нужно провести кубический сплайн;
- вычисляется вектор VK с использованием одной из перечисленных функций;
- вычисляется множество произвольных значений интерполирующей функции в нужном количестве точек с помощью стандартной функции interp.
