Первый замечательный предел

Доказательство

Рассмотрим односторонние пределы и и докажем, что они равны 1.

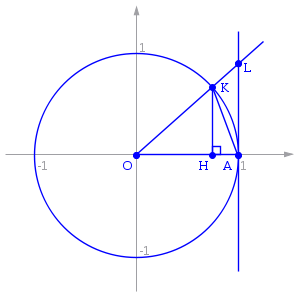
Пусть . Отложим этот угол на единичной окружности (R = 1).

Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX.

Очевидно, что:

(1)

(где S_sectOKA — площадь сектора OKA)

(из : | LA | = tgx)

Подставляя в (1), получим:

Так как при :

Умножаем на sinx:

Перейдём к пределу:

Найдём левый односторонний предел:

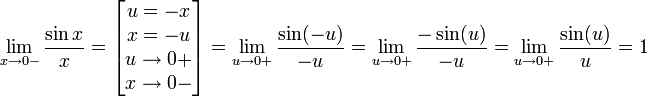
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.

Следствия

• 

• 

• 

• 

Доказательство следствий  [показать]

[Править] Второй замечательный предел

или

Доказательство второго замечательного предела:

Доказательство для натуральных значений x  [показать]

   Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что . Рассмотрим два случая:

1. Пусть . Каждое значение x заключено между двумя положительными целыми числами: , где  — это целая часть x.

Отсюда следует: , поэтому

.

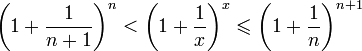Если , то . Поэтому, согласно пределу , имеем:

.

По признаку (о пределе промежуточной функции) существования пределов .

2. Пусть . Сделаем подстановку − x = t, тогда

.

Из двух этих случаев вытекает, что для вещественного x.   

Следствия

1. 

2. 

3. 

4. 

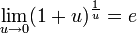
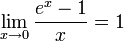
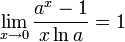5. для ,

6. 

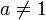
19)Понятие производной. таблица производной

Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием. Обратный процесс — интегрирование.

Определение

Пусть в некоторой окрестности точки определена функция Производной функции называется такое число , что функцию в окрестности U(x₀) можно представить в виде

f(x₀ + h) = f(x₀) + Ah + o(h)

если существует.

[Править] Определение производной функции через предел

Пусть в некоторой окрестности точки определена функция Производной функции f в точке x₀ называется предел, если он существует,

[править] Общепринятые обозначения производной функции y = f(x) в точке x₀

Заметим, что последнее обычно обозначает производную по времени (в теоретической механике).

[Править] Дифференцируемость

Основная статья: Дифференцируемая функция

Производная функции f в точке x₀, будучи пределом, может не существовать или существовать и быть конечной или бесконечной. Функция f является дифференцируемой в точке x₀ тогда и только тогда, когда её производная в этой точке существует и конечна:

Для дифференцируемой в x₀ функции f в окрестности U(x₀) справедливо представление

при

20)Правило дифференцирования