1. Определение матрицы. Арифметические операции над матрицей. Элементарные преобразования матриц.

Матрица — математический объект, записываемый в виде прямоугольной таблицы. Количество строк и столбцов матрицы задают размер матрицы.

Для матрицы определены следующие алгебраические операции:

• сложение матриц, имеющих один и тот же размер;

• умножение матриц подходящего размера (матрицу, имеющую столбцов, можно умножить справа на матрицу, имеющую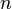строк);

• в том числе умножение матрицы на число;

• транспонирование;

• сколярное произведение;

Элементарными преобразованиями строк называют:

• перестановку местами любых двух строк матрицы;

• умножение любой строки матрицы на константу 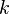,,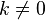 при этом определитель матрицы увеличивается вkраз;

• прибавление к любой строке матрицы другой строки.

2. Определитель матрицы. Свойства-1(определитель с нулевой строкой равен нулю, умножение определителя на число равносильно умножению какой-либо строки/столбца на это число, при перестановке двух строк/столбцов определитель меняет знак, определитель матрицы с двумя одинаковыми строками./столбцами равен нулю)

Определитель (или детерминант) — число, которое соответствует квадраты матрицы (вычисляется по определённому закону).

Свойства

1) Если матрица содержит нулевую строку (столбец), то определитель этой матрицы равен нулю

2) Если в определителе переставить местами любые две строки или два столбца, то определитель изменяет свой знак на противоположный.

3) Умножение всех элементов строки или столбца определителя на некоторое число λ равносильно умножению определителя на это число.

4) Если две строки (столбца) матрицы равны между собой, то определитель этой матрицы равен нулю.

3. Определитель матрицы. Свойства-2 (определитель, содержащий две одинаковые строки или столбца, равен нулю, определитель матрицы не изменится, если к элементам одной строки прибавить элементы другой строки, умноженные на одно и то же число, сумма произведений элементов одной строки матрицы на алгебраические дополнения к элементам другой строки этой матрицы равен нулю, определитель произведения матриц равен произведению определителей этих матриц (на примере матриц 2x2) )

Определи́тель (или детермина́нт) — число, которое соответствует квадраты матрицы (вычисляется по определённому закону).

1) Если две строки (столбца) матрицы равны между собой, то определитель этой матрицы равен нулю.

2) Определитель не изменится, если к элементам любой его строки (или столбца) прибавить соответствующие элементы другой строки (или соответствующего столбца), умноженные на одно и тоже число.

3) ПустьAиB– квадратные матрицы одного и того же порядка. Тогда определитель произведения матриц равен произведению определителей:

4. Формулы для определителей порядка 2x2, 3x3

1) определитель матрицы 2х2 = a₁₁*a₂₂ -a₂₁*a₁₂ ;

2) определитель матрицы 3х3 – правило «Звездочки» Саррюса

5. Вычисление определителя разложением по строке / столбцу

Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.

Разложив по первой строке, вычислить определитель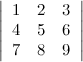 

Решение. 

Ответ.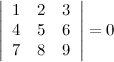 

6. Вычисление определителя методом Гаусса

Для вычисления определителя матрицы методом Гаусса необходимо привести матрицу к треугольному виду. 

Алгоритм метода Гаусса

1)ведущий элемент –a_11, ведущая строка – первая. С помощью ведущей строки обнуляем элементы под ведущими элементами(элементы 1го столбца под главной диагональю)

2) ведущий элемент – а_22, ведущая строка – вторая. И тд, как в п. 1.

7. Обратная матрица – определение, 5 свойств

Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:

Матрица  называется обратной для матрицы , определитель которой отличен от нуля , если справедливы равенства , где E – единичная матрица порядкаn на n.

Свойства обратной матрицы:

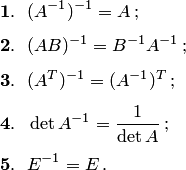
8. Теорема о существовании обратной матрицы

Теорема. (о существовании обратной матрицы). Для того чтобы для квадратной матрицы  существовала обратная матрица, необходимо и достаточно, чтобы матрица  была невырожденной.

В процессе доказательства этой теоремы построен алгоритм нахождения обратной матрицы, который заключается в следующем:

1) находится определитель матрицы . Если , то обратной матрицы не существует. Если , то обратная матрица существует;

2) вычисляются алгебраические дополнения для всех элементов матрицы ;

3) составляется присоединенная для матрица, обозначаемая *, размещением алгебраических дополнений элементов каждой строки матрицы  в соответствующий по номеру столбец матрицы *:

;

 

 

 

4)      выписывается обратная матрица по формуле

т.е. присоединенную матрицу надо умножить на величину .