14. Решение слау с квадратной невырожденной матрицей методом Гаусса (прямой обратный ход)

ешите систему линейных уравнений  методом Гаусса.

Решение.

Исключим неизвестную переменную x₁ из второго и третьего уравнения системы. Для этого к обеим частям второго и третьего уравнений прибавим соответствующие части первого уравнения, умноженные на  и на  соответственно:

Теперь из третьего уравнения исключим x₂, прибавив к его левой и правой частям левую и правую части второго уравнения, умноженные на :

На этом прямой ход метода Гаусса закончен, начинаем обратный ход.

Из последнего уравнения полученной системы уравнений находим x₃:

Из второго уравнения получаем .

Из первого уравнения находим оставшуюся неизвестную переменную и этим завершаем обратный ход метода Гаусса .

Ответ:

x₁ = 4, x₂ = 0, x₃ = -1.

Определение

15. Решение слау с квадратной невырожденной матрицей методом Крамера.

Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений (СЛАУ) с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и оно единственно).

При решении СЛАУ методом Крамера используется вычисление определителя или детерминанты основной матрицы. Для того, чтобы систему уравнение можно было решить методом Крамера, необходимо и достаточно, чтобы определитель ее основной матрицы был отличен от нуля, тоесть матрица должна быть невырожденной.

16. Решение слау с квадратной невырожденной матрицей с помощью обратной матрицы.

Пример 1.

Найти решение системы

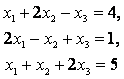
С помощью обратной матрицы.

Выпишем матрицу системы

Найдем присоединенную матрицу Ã. Имеем:

Следовательно,

Вычислим определитель матрицы А с помощью разложения по первой строке:

|A| = 1·(-3) + 2·(-3) + (-1)·3 = -12.

Таким образом,

Отсюда

Тем самым Х1 = 1, Х2 = 2, Х3 = 1.

17. Теорема Кронекера – Капелли .

Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных и бесконечное множество решений, если ранг меньше числа неизвестных.

Необходимость

Пусть система совместна. Тогда существуют числа x1...xn € R  такие, что b= x1a1+....+xnxn. Следовательно, столбец b является линейной комбинацией столбцов a1,...an  матрицы A . Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что rangA=rangB.

Достаточность

Пусть rangA=rangB=r. Возьмем в матрице A какой-нибудь базисный минор. Так как rangB=r , то он же и будет базисным минором и матрицы B. Тогда, согласно теореме о базисном миноре, последний столбец матрицы B  будет линейной комбинацией базисных столбцов, то есть столбцов матрицы A. Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы A .

Следствия

1. Количество главных переменных системы равно рангу системы.

2. Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.