30. Способ вращения вокруг оси, перпендикулярной к плоскости проекций.

Плоскости носитель траекторий перемещения точек параллельны плоскости проекций. Траектория - дуга окружности, центр которой находится на оси перпендикулярной плоскости проекций. Для определения натуральной величины отрезка прямой общего положения АВ (рис. 4.4), выберем  ось вращения перпендикулярную горизонтальной плоскости проекций и проходящую через В₁. Повернем отрезок так, чтобы он стал параллелен фронтальной плоскости проекций (горизонтальная проекция отрезка параллельна оси x). При этом точка А₁ переместиться в А*₁, а точка В не изменит своего положения. Положение точки А*₂ находится на пересечении фронтальной проекции траектории перемещения точки А (прямая линия параллельная оси x) и линии связи проведенной из А*₁. Полученная проекция В₂ А*₂ определяет действительные размеры самого отрезка.

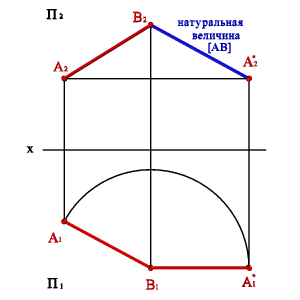
а) модель б) эпюр

31. Способ вращения вокруг оси, параллельной плоскости проекций (вокруг линии уровня).

(Определить натуральную величину ∆ABC во вращении вокруг линии уровня. - - -

При помощи методов преобразования можно определить натуральные величины сечения поверхности.

Определить натуральную величину сечения поверхности плоскостью.)

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

 Этот способ применяется в основном для решения задачи преобразования плоскости общего положения в плоскость уровня. Суть способа заключается в том, что плоскость общего положения, поворачивается вокруг прямой уровня до состояния, параллельного горизонтальной плоскости проекций П₁ либо фронтальной П₂.

 Рассмотрим поворот точки А вокруг горизонтали a до уровня горизонтали. Точка А движется по дуге окружности радиуса R с центром в точке O, принадлежащей горизонтали a. Радиус R является гипотенузой прямоугольного треугольника А₀А₁O, где один катет А₁О - горизонтальная проекция радиуса вращения, другой - равен Dz - расстояние между точкой A и прямой a по вертикали. А' - новое положение точки А.

Алгоритм графических построений:

1. Через А₁ проводим горизонтальную проекцию дуги по которой поворачивается точка А. Это будет прямая, перпендикулярная прямой a₁;

Н а пересечении прямой a и проекции дуги отмечаем точку O₁;

2. Строим прямоугольный треугольник A₁A₀O₁. Попутно мы решили задачу нахождения расстояния между прямой и точкой. Отрезок A₀O₁ - расстояние от точки A до прямой a;

3. Обратите внимание, на то, что построения, выполняемые на верхнем демонстрационном чертеже выполняются в вертикальной плоскости, а на ортогональном чертеже мы делаем те же построения, только в горизонтальной плоскости. На результат построений такой прием не влияет;

4. Проводим дугу A₀A₁' с центром в точке O₁. А₁' - новая проекция точки А;

5. Подняв от A₁' линию проекционной связи до пересечения с a₂ находим A₂'.

32. Способ плоско-параллельного перемещения.

При использовании способа параллельного движения фигуры приводится в частное положение перемещением в пространстве относительно неподвижной системы плоскости проекции П₁, П₂ и находим новые проекции фигуры на П₁ и П₂.

 Плоскопараллельным перемещением фигур в пространстве называется такое ее перемещение, при котором все точки фигуры перемещаются в параллельном пространстве. При этом строят новые проекции на П₁ и П₂.

 Рассмотрим плоскопараллельное движение треугольника. Пусть треугольник АВС совершает плоскопараллельное движение относительно горизонтальной плоскости проекции. Тогда его вершины перемещаются в горизонтальных плоскостях, а угол наклона плоскости треугольника к П₁ при плоскопараллельном движении фигуры относительно горизонтальной плоскости проекций не меняется. Горизонтальная проекция фигуры остается равной самой себе, а горизонтальные проекции ее тоже перемещаются по прямым, перпендикулярным линиям связи.

 Аналогично при плоскопараллельном перемещении относительно П₂ ортогональная проекция фигуры остается равной самой себе, а горизонтальные проекции ее точек перемещаются по прямым, перпендикулярным линиям связи.