33. Векторное произведение векторов.

Векторным произведением вектора   на вектор   называется вектор, обозначаемый символом   и определяемый следующими тремя условиями:

1. Модуль вектора   равен  , где   - угол между векторами   и  ;

2. Вектор   перпендикулярен к каждому из вектора   и  ;

3. Направление вектора   соответствует «правилу правой руки». Это означает, что если векторы  ,   и   приведены к общему началу, то вектор   должен быть направлен так, как направлен средний палец правой руки, больой палец которой направлен по первому сомножителю (то есть по вектору  ), а указательный - по второму (то есть по вектору  ).

Векторное произведение   обращается в нуль тогда и только тогда, когда векторы   и   коллинеарны. В частности,  .

Если система координатных осей правая и векторы   и   заданы в этой системе своими координатами:

,  ,

то векторное произведение вектора   на вектор   определяется формулой ,

или

.

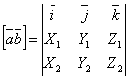5. Скалярное произведение векторов и угол между ними.

Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.

Если векторы   и   заданы своими координатами: ,  ,то их скалярное произведение может быть вычислено по формуле

.Отсюда следует необходимое и достаточное условие перпендикулярности двух векторо .

Угол   между векторами

дается формулой  , или в координатах

.

34. Смешанное произведение векторов.

Тройкой векторов называются три вектора, если указано, какой из них считается первым, какой вторым и какой третьим. Тройку векторов записывают в порядке нумерации; например, запись  ,  ,   означает, что вектор   считается первым,   - вторым,   - третьим.

Тройка некомпланарных векторов  ,  ,   называется правой, если составляющие ее векторы, будучи приведены к общему началу, располагаются в порядке нумерации аналогично тому, как расположены большой, указательный и средний пальцы правой руки. Если векторы  ,  ,   расположены аналогично тому, как расположены большой, указательный и средний пальцы левой руки, то тройка этих векторов называется левой.

Смешанным произведением трех векторов  ,  ,   называется число, равное векторному произведению  , умноженному скалярно на вектор  , то есть  .

Если векторы  ,  ,   заданы своими координатами: ,  , то смешанное произведение   определяется формулой

.

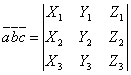25. Уравнение прямой на плоскости.

1. Ах + Ву + С = 0 – общее уравнение прямой.

• C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат

• А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох

• В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу

• В = С = 0, А ≠0 – прямая совпадает с осью Оу

• А = С = 0, В ≠0 – прямая совпадает с осью Ох

2. Найти уравнение прямой, проходящей через точку А(1, 2) и перпендикулярно к вектору нормали (3, -1). Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А. Получаем: 3 – 2 + C = 0, следовательно С = -1. Итого: искомое уравнение: 3х – у – 1 = 0.

3. Пусть в пространстве заданы две точки M ₁ ( x ₁ , y ₁ , z ₁ ) и M₂ ( x ₂, y ₂ , z ₂ ), тогда уравнение прямой, проходящей через эти точки:

Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.На плоскости записанное выше уравнение прямой упрощается:

Дробь  = k называется угловым коэффициентом прямой.

4. Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:   иобозначить  , то полученное уравнение называется 

уравнением прямой с угловым коэффициентом k .

5. Каждый ненулевой вектор  ( α₁ , α₂ ), компоненты которого удовлетворяют условию А α₁ + В α₂ = 0 называется направляющим вектором прямой.

6. Уравнение прямой в отрезках: , где

7. Если обе части уравнения Ах + Ву + С = 0 разделить на число  , которое называется нормирующем множителем , то получим

xcosφ + ysinφ - p = 0 –нормальное уравнение прямой.

Знак ± нормирующего множителя надо выбирать так, чтобы μ ? С < 0.

р – длина перпендикуляра, опущенного из начала координат на прямую, а φ - угол, образованный этим перпендикуляром с положительным направлением оси Ох.

8. Прямая, проходящая через точку М₁ (х₁ , у₁ ) и перпендикулярная к прямой у = kx + b представляется уравнением:

9. Угол между прямыми на плоскости.

Если заданы две прямые y = k₁ x + b₁ , y = k ₂x + b₂ , то острый угол между этими прямыми будет определяться как .

Две прямые параллельны, если k₁ = k₂ . A1\A2 = B1\B2. Две прямые перпендикулярны, если k₁ = -1/ k₂ . A1A2+B1B2 = 0

10.Расстояние от точки до прямой. Если задана точка М(х₀ , у₀ ), то расстояние до прямой Ах + Ву + С =0 определяется как

11. Каноническое уравнение: