§10. Степенные ряды.

Функциональный ряд вида , где называется степенным рядом по степеням .

С помощью замены получим ряд . Исходный получается обратной заменой из данного.

Теорема Абеля (о сходимости степенных рядов). Для всякого степенного ряда существует неотрицательное число R ( возможно ) такое, что ряд сходится абсолютно при - сходится равномерно при - расходится при .

Доказательство. Ряд заведомо сходится при x=0. Если других точек сходимости нету, то очевидно число R=0.

Предположим, что (область сходимости). Так как ряд - сходится, то согласно признаку сходимости общий член ряда . Это означает, что последовательность , будучи сходящейся, ограничена, т.е. , так что пусть x такой, что . (в силу оценок полученных выше) - сходится как сумма геометрической прогрессии ( ).

Получаем, что данный степенной ряд сходится абсолютно при любом x, таком, что .

Отсюда видно, что в качестве R можно взять (D- область сходимости).

При - ряд расходится, поскольку мы оказываемся за пределами границы области сходимости.

Если , то . Тогда получаем, что - мажоритарный ряд для , который сходится , так как это геометрическая прогрессия ( ). Значит данный ряд сходится равномерно в указанной области согласно признаку Вейерштрасса.

Замечание. Число R, о котором идет речь в условии теоремы, называется радиусом сходимости данного функционального ряда. Интервал (-R; R), внутри которого ряд сходится абсолютно называется интегралом сходимости.

Степенной ряд по степеням ( ) то он имеет интервал сходимости ( ).

Кроме интервала сходимости в область сходимости могут входить края.

2. Свойства степенных рядов.

1. Сумма степенного ряда непрерывна на интервале сходимости (причем ).

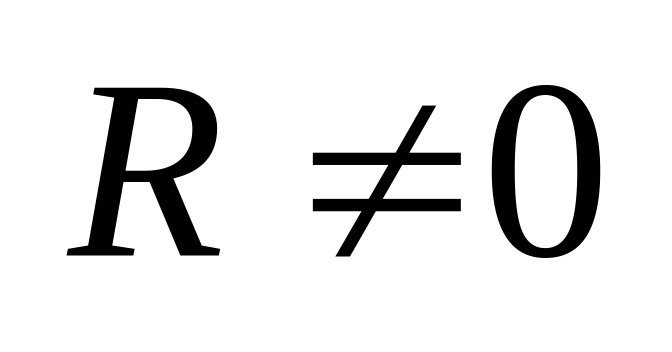Доказательство. Пусть - интервал сходимости: . . По теореме Абеля ряд сходится равномерно на и, значит, сумма его непрерывна во всех точках данного отрезка, в частности, в точке x.

2. Операция почленного дифференцирования и интегрирования по любому отрезку от 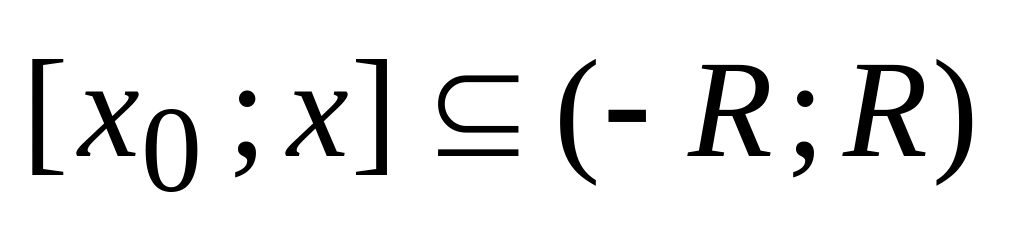степенного ряда не имеет его радиуса сходимости.

Доказательство. Предположим, что существует предел . Рассмотрим ряд полученный почленным дифференцированием ряда , получим .

Пусть радиус сходимости .

Рассмотрим ряд полученный почленным интегрированием x

.

Второй ряд из этих двух является числовым и он сходится, поскольку сходится, т.к. интервалу сходимости.

Вычислим (радиус сходимости первого ряда). .

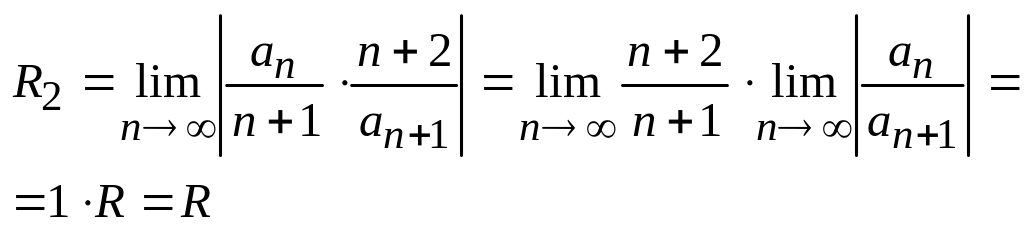3. Степенной ряд можно любое количество раз дифференцировать на отрезке сходимости .

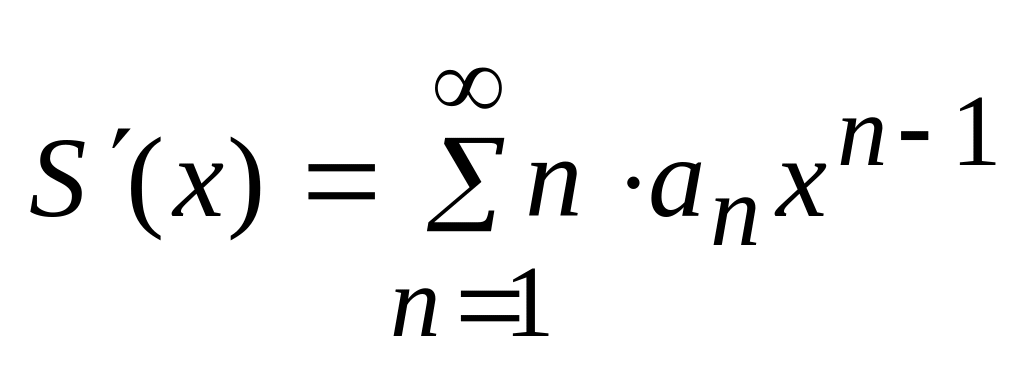Доказательство. Вытекает из теоремы о почленном дифференцирование функциональных рядов.

4. Степенной ряд можно почленно интегрировать любое количество раз по любому отрезку .

§11. Ряды Тейлора.

Пусть функция - бесконечно дифференцирован в окрестности точки (т.е существует производная). Поставим этой функции в соответствие ряд 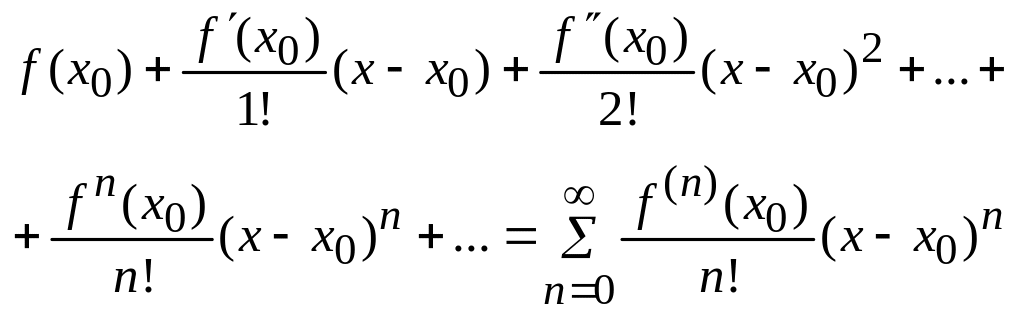. Данный ряд называется рядом Тейлора функции в окрестности точки . В частном случае, когда , получаем - ряд Маклорена функции .

Замечание 1. Ряд Тейлора является степенным рядом, следовательно имеет радиус сходимости и интервал сходимости. Однако сумма ряда необязательно совпадает с функцией . За пределами интервала сходимости сумма проста не существует.

Если же сумма ряда на то говорят, что функция разложима в ряд Тейлора в окрестности точки .

Замечание 2. Частичные суммы ряда Тейлора представляются следующими многочленами: 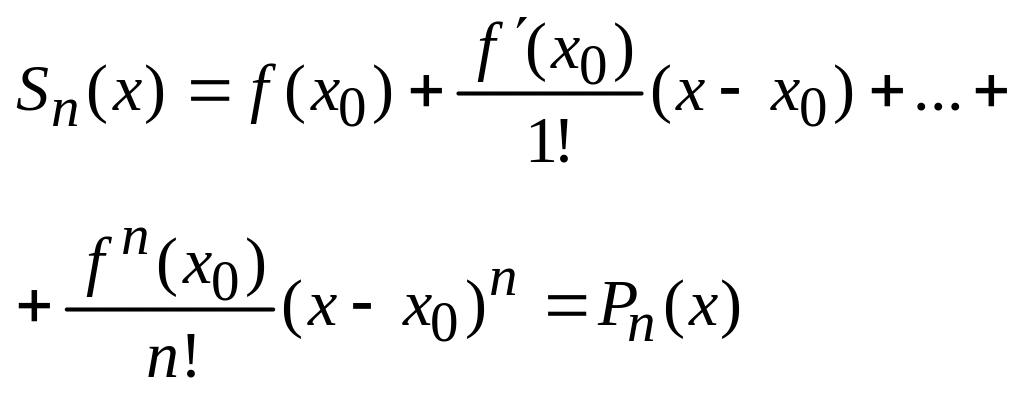, которые есть ничто иное, как многочлены Тейлора (обозначим их через P(x)).

Существует формула Тейлора, которая имеет вид: , где -остаток формулы Тейлора. Для остатка были получены следующие оценки: - оценка остатка в форме Пеана, а также , где точка расположена между x₀ и x. Оценка остатка формулы Тейлора в форме Лагранжа.

Обозначим через - остаток ряда Тейлора. Вообще говоря и не одно и тоже. Действительно и формула Тейлора одно и тоже.

Но если , т.е. функция - разложима в ряд Тейлора, то остаток ряда Тейлора совпадает с остатком формулы Тейлора.

Это позволяет для оценки остатка ряда Тейлора использовать оценки остатка формулы Тейлора.

Теорема 1. Для того, чтобы бесконечно дифференцированная функция разложилась в ряд Тейлора в окрестности точки .

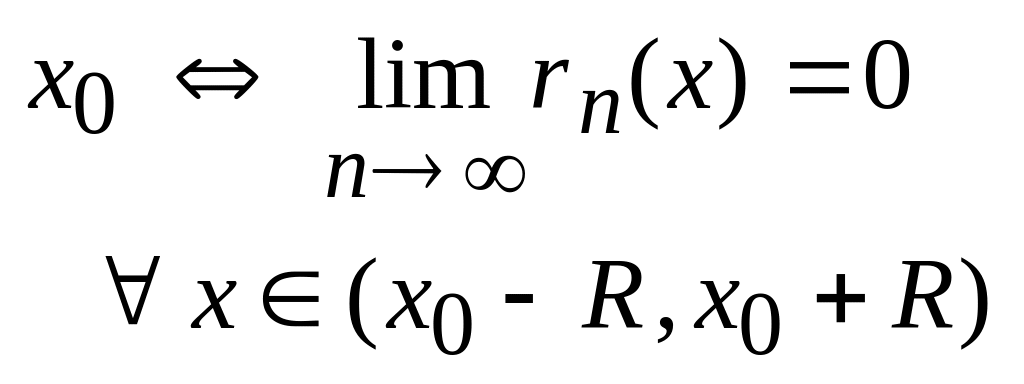Доказательство. Мы уже отметили, что разложение означает , а это в свою очередь .

Теорема 2 (достаточный признак разложения в ряд Тейлора). Если , все производные функции ограничены одной и той же константой M (это свойство называется равномерной ограниченностью на данном интервале), то ряд Тейлора функции - сходится к функции .

Доказательство. Воспользовавшись теоремой 1 покажем, что . Применим формулу Лагранжа, для оценки остатка формулы Тейлора. Имеем:

.

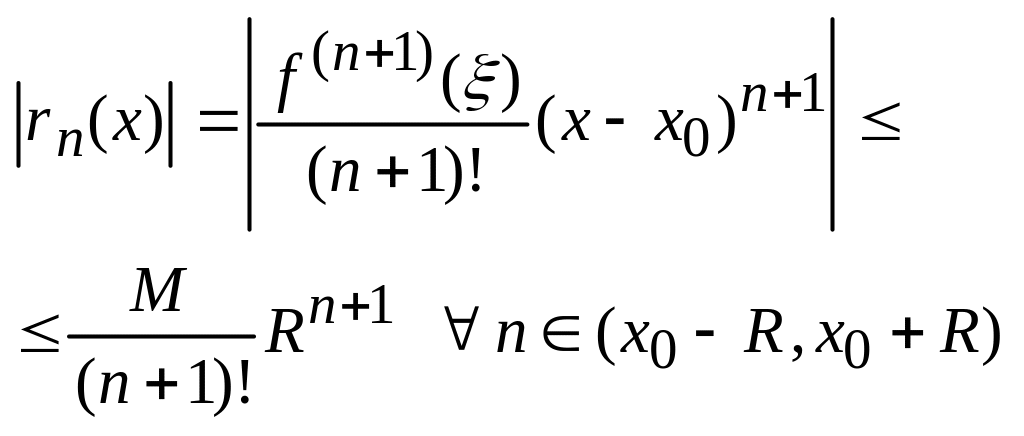Числовой ряд - сходится по признаку Д’Аламбера, то согласно необходимому признаку сходимости. Предел .

Таким образом и . Следовательно ввиду оценки и .

Теорема 3 Если степенной ряд по степеням - сходится к функции в окрестности точки , то он является рядом Тейлора для данной функции.

Доказательство. Пусть Согласно свойствам степенной ряд можно любое количество раз почленно дифференцировать в окрестности точки .

.

После дифференцирования:

Из полученных равенств находим, что .

Т.е. коэффициенты совпадают с коэффициентом ряда Тейлора.

……………

………………

.