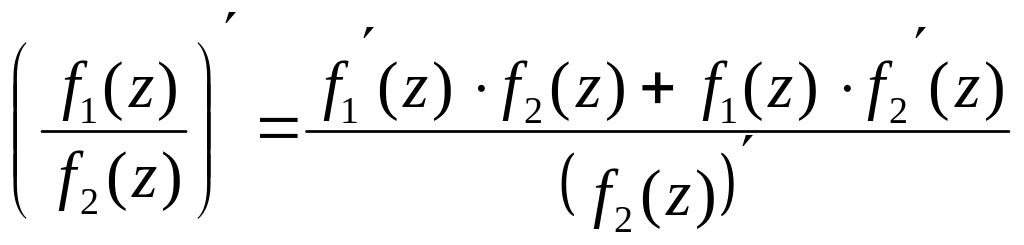Функции комплексных переменных.
Основные определения и понятия.
Пусть даны 2 комплексные плоскости:
Р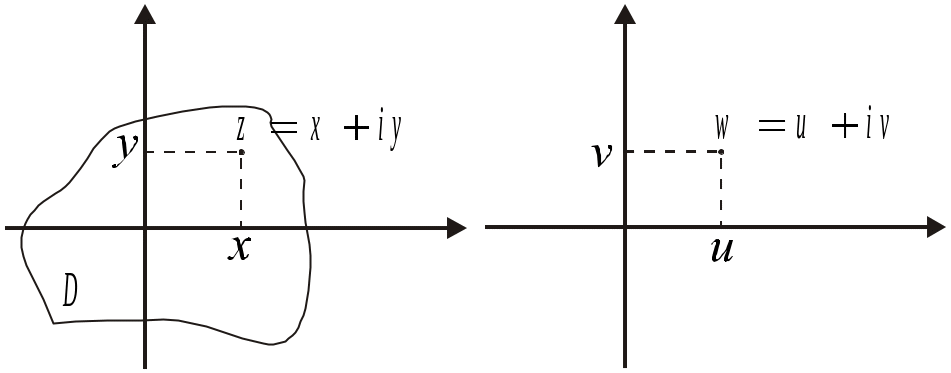
ассмотрим
некоторую область D
на 1 плоскости. Если каждой точке z
из множества D ставится
в соответствие некоторая точка w
из 2 плоскости, то говорят, что на множестве
D задана однозначная
функция комплексных переменных. (D
– область определения функции).
Всякую функцию можно представить в виде
;
где
-
две вещественно значные функции
действительных функций от двух переменных.
Они соответственно называются вещественной
и мнимой частью данной комплексно
значной функции.
Если каждому комплексному числу
ставится в соответствие несколько
комплексных чисел, то такое соответствие
называется многозначной функцией
комплексных переменных.
Для однозначных функций комплексных переменных вводят понятия предела, непрерывности, и т.д. А именно:
Если для
,
такая, что
(*) то число A
называется пределом функции
в точке
:
.
Если перейти к действительным и мнимым числам:
Нетрудно видеть, что оно равносильно следующему
Комплексная
функция
имеет предел:
Различные свойства пределов действительных переменных, сохраняет свойства обычных пределов:
Аналогично определим непрерывность:
Функция
называется непрерывной в
,
если она определена в этой точке имеет
в ней предел, который совпадает со
значением функции.
Это условие равносильно тому, что предел
т.е. вещественные
и мнимые части
-
непрерывны в точке
.
Справедливы все свойства непрерывности пределов, которые имеют место для действительных функций.
Элементарные функции комплексных переменных.
Под элементарными функциями комплексных переменных понимают функции, которые можно представить в как сумму степенного ряда по степеням комплексных переменных z.
Показательная функция
Естественно определим, что и для комплексных переменных должно быть разложение в такой же ряд
В частности для чисто мнимого аргумента z получим
Выделим отдельно мнимые и действительные части
-
формула Эйлера.
.
Логарифмическая функция
Пусть
,
- эта функция многозначная.
- главное значение логарифма.
Тригонометрическая функция
В
результате разложения в ряд следующих
функции
,
можно заметить следующее:
Из
системы находим
и
.
…
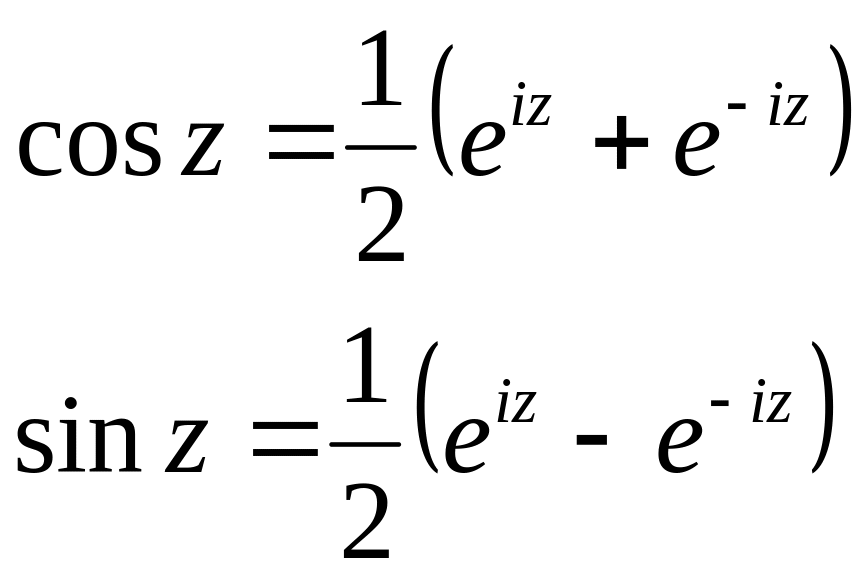
Отметим,
что
является периодической с периодом
;
-
также являются периодическими с периодом
.
Пример.
Гиперболическая функция
Обратные тригонометрические функции
- нужно решить это уравнение относительно
.
Обобщенная показательная функция
Обобщенные степенные функции
§2. Дифференцирование и интегрирование функций комплексных переменных.
1. Производная функции комплексных переменных.
Пусть
задана
в окрестности ࠔ
.
Окрестность
если существует
- которая называется производной
функции z в точке
.
И обозначается
.
Функция
называется дифференциалом в
точке
.
Если
функция
дифференцируема во всей области
,
то функция f-
дифференцируема на множестве D.
Из условия дифференцирования вытекает следующее равенство:
.
Главная
часть приращения:
-
дифференциал функции
.
Из определения свойств пределов к комплексных переменных вытекают свойства производных.
Свойства производных:
Для основных элементарных функций таблица производных такая же как и для функций действительных переменных.