2. Интегральная теорема Коши.

Теорема. Если - аналитическая в замкнутой односвязной области D с границей Г, то интеграл по контуру Г: .

Доказательство.

Если , то

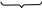
= {Для таких интегралов существует формула Грина } = .

0 По условию 0

Коши-Римана

Обобщением выше сказанного является следующая теорема.

Теорема. Пусть аналитическая в замкнутой многосвязной области D с внешним контуром Г, и внутренним контурами : . Все контуры ориентированны одинаково, тогда .

3. Интеграл с переменным верхним пределом и неопределенным интегралом.

В силу условий Коши-Римана интегралы во второй части не зависят от пути интегрирования. Это означает, что результат зависит от начальной и конечной точки.

Г может быть любой путь в области D, где функция аналитическая.

- интеграл с переменным верхним пределом.

Теорема. Если функция аналитическая в односвязной области D, то функция также аналитическая в односвязной области D. Или производная .

Такая функция называется первообразной функции .

Можно показать, что различные первообразные одной и той же функции отличаются лишь на константу. Совокупность всех первообразных функции называют неопределенным интегралом этой функции: .

Можно показать, что для интегралов от комплексно интегральной функции справедлива формула Ньютона-Лейбница: .

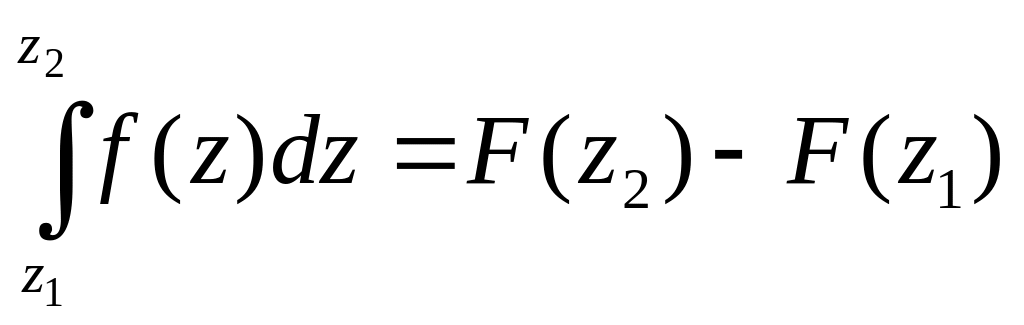4. Интегральная формула Коши.

Теорема. Пусть функция - аналитическая в замкнутой односвязной области D с границей Г, тогда для любой внутренней точки z области D: - формула Коши (интеграл Коши).

Доказательство.

Рассмотрим интеграл Коши z – фиксированная точка.

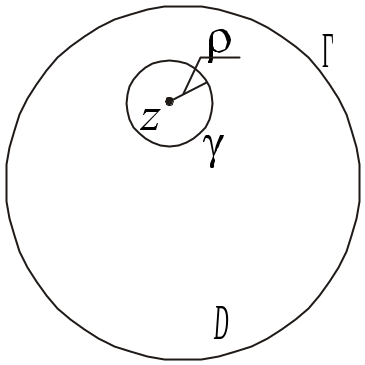
Если вырезать из D данный круг, то получится двухсвязная область, в которой подынтегральная функция аналитическая везде, тогда согласно интегральной теореме Коши для многосвязной области: {Выбирая ρ (радиус) –маленький, можно показать, что подынтегральная функция ; то и весь 1 интеграл стремится к 0, то } .

Замечание (интегральная формула Коши для многосвязной области).

Если - аналитическая в многосвязной области D с внешним контуром Г, и внутренним контурами , то для любой внутренней точки :

5. Бесконечная дифференцируемость аналитических функций. Интегральные формулы для производных.

Пусть функция - аналитическая в замкнутой односвязной области D с границей Г, . Для аналитический функции вычислим .

Итак,

………

Эти формулы означают, что аналитическая в односвязной области функция имеет производные любого порядка.

§4. Ряды в комплексной области.

Большинство свойств для сходимости функций комплексных переменных сохраняется. В частности для степенных рядов теорема Абеля о существовании радиуса сходимости.

, если

Любую аналитическую комплексно значимую функцию можно единственным образом разложить в ряд Тейлора. При этом есть , .

Справедливы также формулы Маклорена для основных функций.

1. Ряды Лорана.

Р яды Лорана – обобщение степенных рядов, когда допускается существование слагаемых с отрицательными степенями: .

главная правильная

часть часть

Если , то ряд Лорана превращается в обычный числовой ряд.

2. Cходимость рядов Лорана.

Как уже отмечалось для степенного ряда существует радиус сходимости, который определяет круг сходимости. Для правильной части . Пусть , тогда главная часть и для него существует ряд сходимости ρ: .

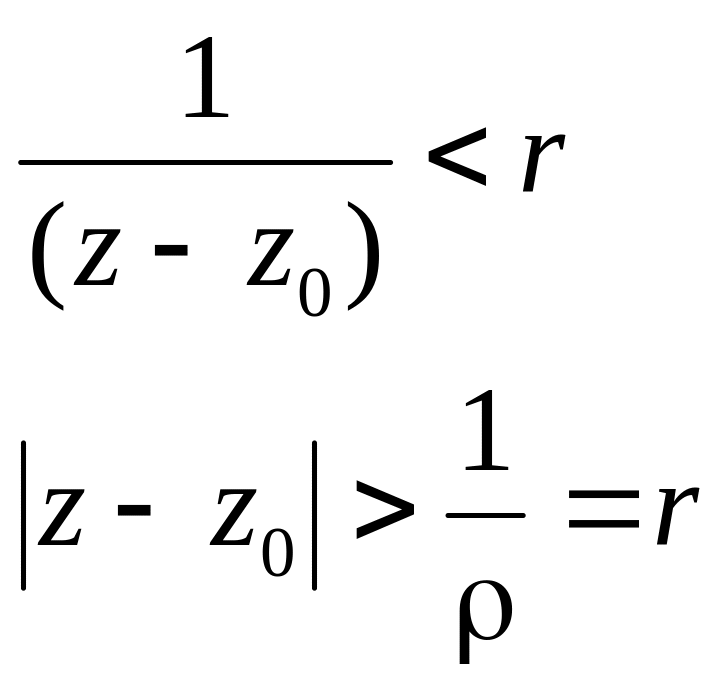Если , то ряд Лорана будет сходится, если , то это кольцо с центром в .

В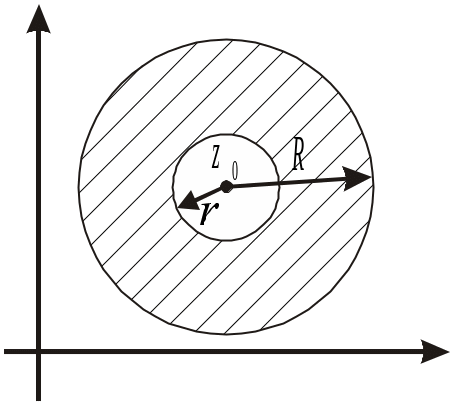 сякую можно разложить в ряд Лорана внутри колец.