§8. Признаки условной сходимости. Особенности условно сходящихся рядов.

Теорема Дирихле (признак Дирихле). Если частичная сумма a_n ряда образует ограниченную последовательность, кроме того последовательность {b_n} монотонно убывает и , то ряд - сходится.

Признак Лейбница является частным случаем данной теоремы.

Теорема Абеля. Пусть ряд - сходится и {b_n} монотонно убывающая последовательность состоящая из положительных членов. Тогда ряд - сходится.

Теорема Римана. Пусть ряд -сходится условно и его сумма: , тогда существует такая перестановка членов данного ряда после которой исходный ряд сходится и его сумма = S.

§9. Функциональные ряды.

Пусть u₁(x), u₂(x)…- последовательность функций, определенных на множестве X. - называется функциональным рядом.

Для всякого числа ряд - обычный числовой ряд.

Если данный числовой ряд сходится, то x₀ – точка сходимости данного функционального ряда. Множество всех точек сходимости называется областью сходимости функционального ряда (D). .

Функция называется n-ой частичной суммой данного ряда, а функция называется суммой данного ряда. Функция определена на множестве D.

- n-ый частичный остаток данного ряда. Переходя к пределу видим, что .

Сходимость о которой идет речь выше называется поточечной сходимостью.

Если сходящийся ряд в какой-то точке x_n, то такая сходимость называется абсолютной.

Множество D₁ точек x₀ в которых ряд сходится абсолютно называется областью абсолютной сходимости ряда .

2. Равномерная сходимость функциональных рядов.

Функциональный ряд называется равномерно сходящимся в области D к (не зависящее от x),

Дадим параллельную формулировку поточечной сходимости.

Ряд называется поточечно сходящимся к сумме в области D, если (вообще говоря зависящее от x), такой что .

3. Признак Вейерштрасса.

Теорема. Если для функционального ряда , причем ряд - сходится. Тогда функциональный ряд сходится равномерно на множестве D.

Доказательство. Обозначим через n-ый частичный остаток , а через n-ый частичный остаток . Так как ряд - сходится , т.е. (не зависящее от x) такой что .

В силу условия теоремы ; . Ряд сходится равномерно на D.

Числовой ряд в формулировке теоремы называется мажоритарным рядом для данного функционального мажорантой. Функциональный ряд для которого существует мажоранта называется мажорируемым.

Достаточным признаком равномерной сходимости функционального ряда являются мажоранты, которые сходятся.

Данный признак достаточный, но не необходимый. Это значит, что если мажоранты не существуют, то нельзя говорить о том, что ряд сходится.

4. Свойства равномерно сходящихся рядов.

Теорема 1 (о непрерывности суммы равномерно сходящихся рядов). Если на множестве D функциональный ряд с непрерывными членами сходится равномерно, то его сумма S(x) непрерывна на этом множестве.

Доказательство. Согласно определению равномерной сходимости для (не зависящий от x) такой что 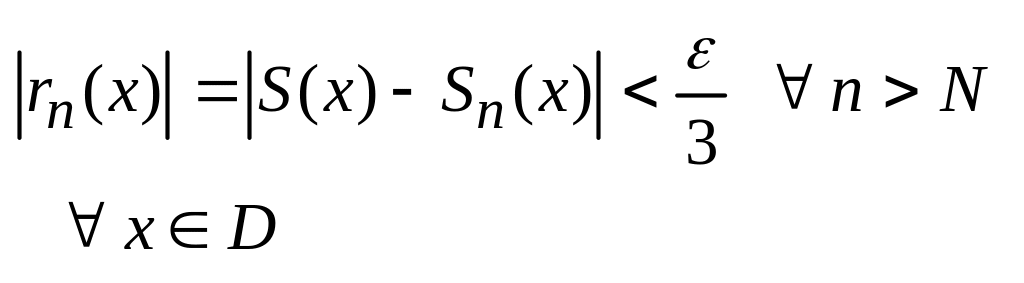. Пусть , для условие выполняется.

Функция непрерывна на множестве D. Как конечная сумма непрерывных функций. Для любого и для выбранного такое что (определение непрерывности ).

Тогда для выбранного

.

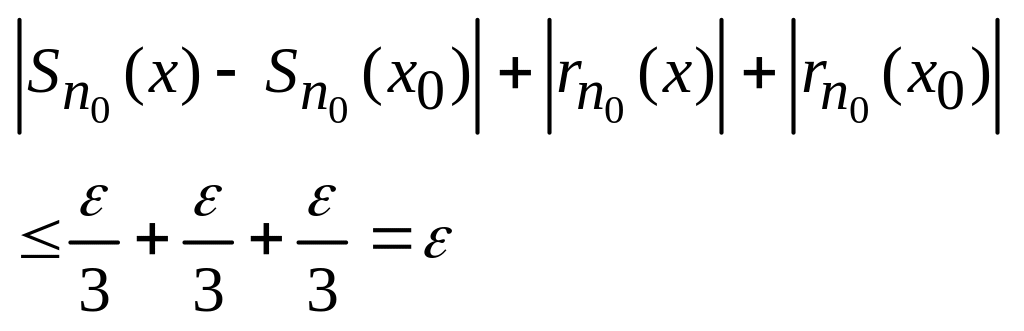Теорема 2 (о почленном интегрировании равномерно сходящихся рядов).

Если функциональный ряд сходится к функции S(x) равномерно на отрезке , то его можно почленно интегрировать по любому отрезку и справедливо равенству 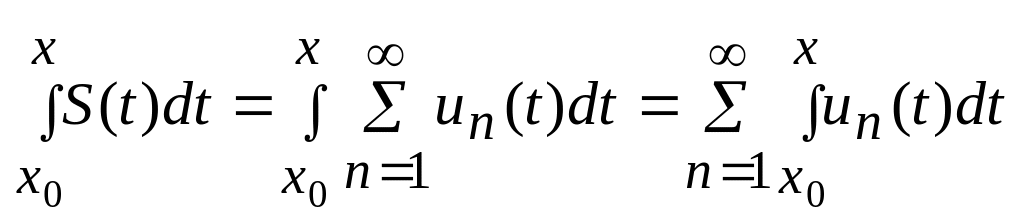, причем последний ряд сходится равномерно на отрезке .

Доказательство. В силу равномерной сходимости данного функционального ряда для (не зависит от x), такой что .

Тогда . Справедливо . А это означает, что ряд 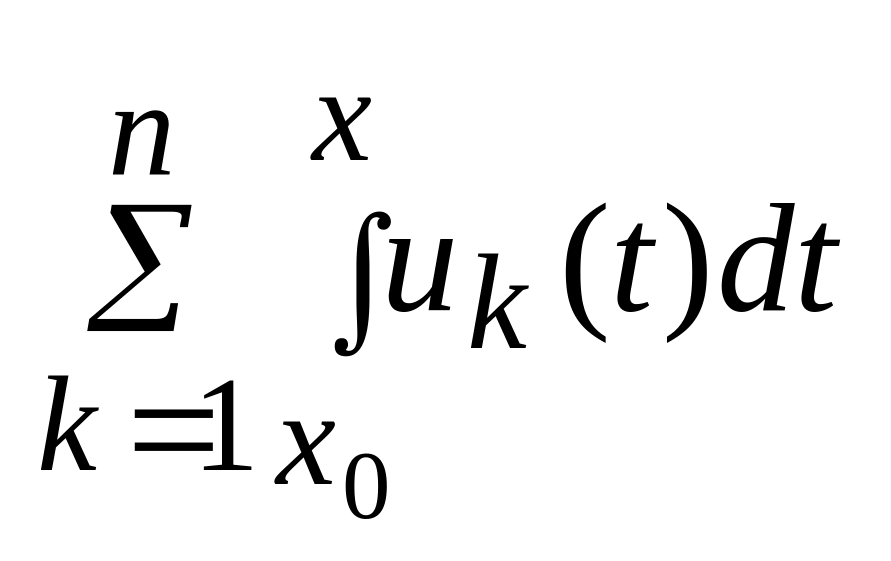- сходится равномерно на к .

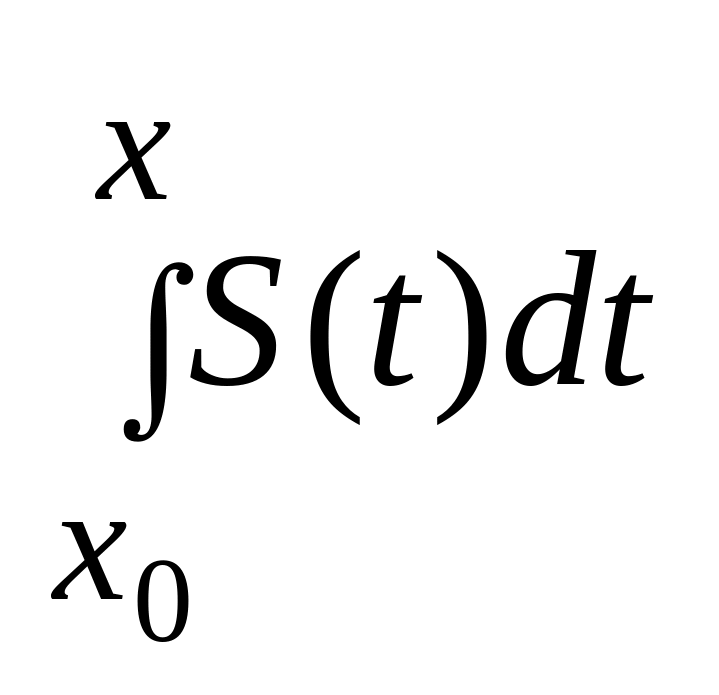Теорема 3 (о почленном дифференцировании равномерно сходящихся рядов). Если ряд сходится на отрезке к сумме S(x).Члены ряда дифференцированы на отрезке и ряд сумма - сходится на - равномерно, то данный ряд так же сходится на равномерно, причем его сумма дифференцирована на и выполняется равенство . (*)