
- •§1. Числовые ряды.
- •Основные понятия. Примеры.
- •2. Простейшие свойства числовых рядов.
- •§2. Необходимые условия сходимости числового ряда. Гармонический ряд.
- •§3. Признаки сходимости рядов с неотрицательными членами.
- •§4.Признаки д’ Аламбера и Коши сходимости знакоположительных числовых рядов.
- •§5. Интегральный признак сравнения.
- •§6,7. Знакопеременные ряды. Знакочередующиеся ряды. Признак Лейбница.
- •§8. Признаки условной сходимости. Особенности условно сходящихся рядов.
- •§9. Функциональные ряды.
- •2. Равномерная сходимость функциональных рядов.
- •Признак Вейерштрасса.
- •4. Свойства равномерно сходящихся рядов.
- •§10. Степенные ряды.
- •2. Свойства степенных рядов.
- •§11. Ряды Тейлора.
- •§12. Разложение функций в ряд Тейлора (Маклорена).
- •§1. Числовые ряды.
§4.Признаки д’ Аламбера и Коши сходимости знакоположительных числовых рядов.
Теорема 1
(признак Д’Аламбера). Пусть
,
![]() и пусть существует
и пусть существует
![]() ,
тогда:
,
тогда:
Если L<1 - сходится.
Если L>1 - расходится.
Доказательство.
Согласно определению интеграла для
![]() такой, что
такой, что
![]() .
.
Пусть L<1, тогда можно выбрать
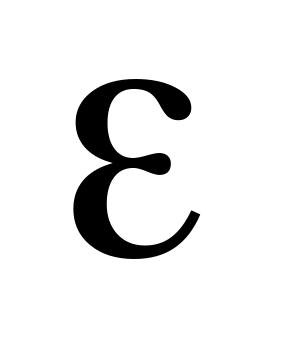 такое, что
такое, что
 ,
так как an>0
an+1<qan
,
так как an>0
an+1<qan
 в частности
в частности
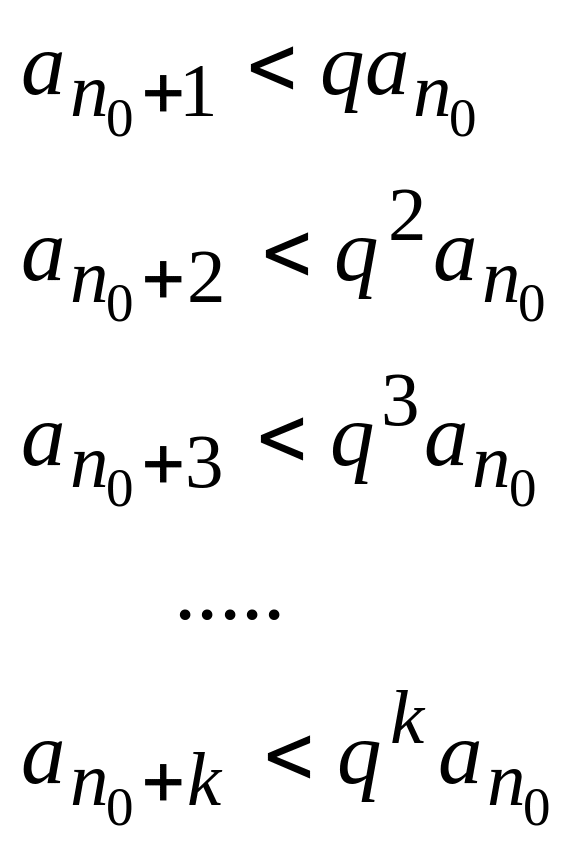 .
.
Рассмотрим
ряд, членами которого являются правые
части
![]() -
геометрическая прогрессия со знаменателем
-
геометрическая прогрессия со знаменателем
![]() сходится, значит согласно теореме 3
сходится ряд
сходится, значит согласно теореме 3
сходится ряд
и из левых частей
![]() (но этот ряд равен исходному) =
(но этот ряд равен исходному) =
![]() что
сходится
что
сходится
![]() .
.
Пусть L>1
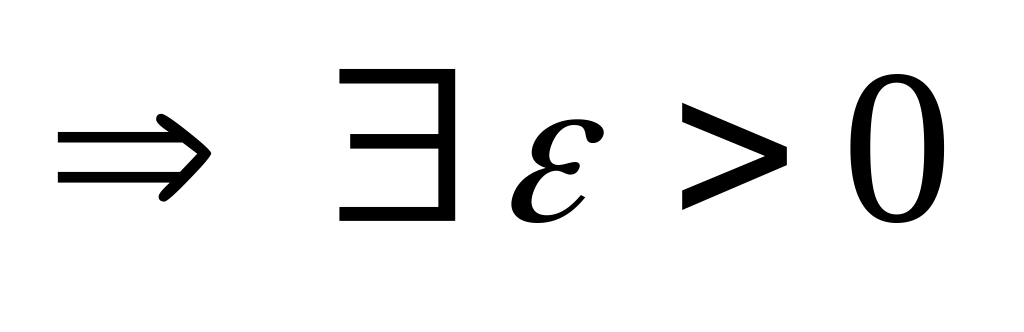 ,
такой, что
,
такой, что
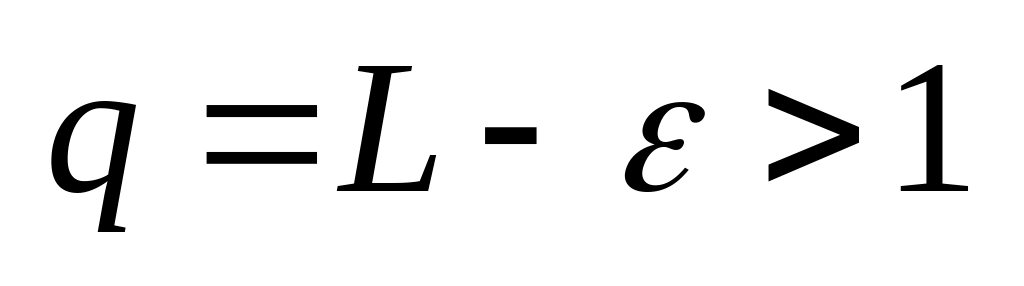 согласно левой части неравенства
получаем, что
согласно левой части неравенства
получаем, что
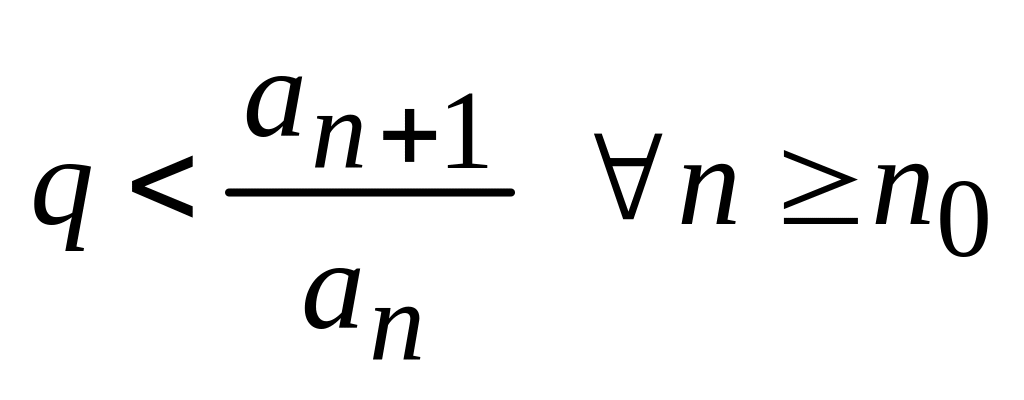 .
.
![]()
![]() ,
т.к. q>1.
,
т.к. q>1.
Это означает, что
последовательность {an}
– не убывающая по крайней мере начиная
с номера n0 тем
самым
![]() тогда не выполняется необходимый признак
сходимости и значит ряд расходится.
тогда не выполняется необходимый признак
сходимости и значит ряд расходится.
Теорема 2
(признак Коши). Пусть
,
![]() и пусть предел
и пусть предел
![]() тогда:
тогда:
Если L<1 - сходится.
Если L>1 - расходится.
Доказательство.
Согласно определению предела для
![]() существует
такой, что
существует
такой, что
![]() .
.
Пусть L<1;
 можно подобрать так, чтобы
можно подобрать так, чтобы
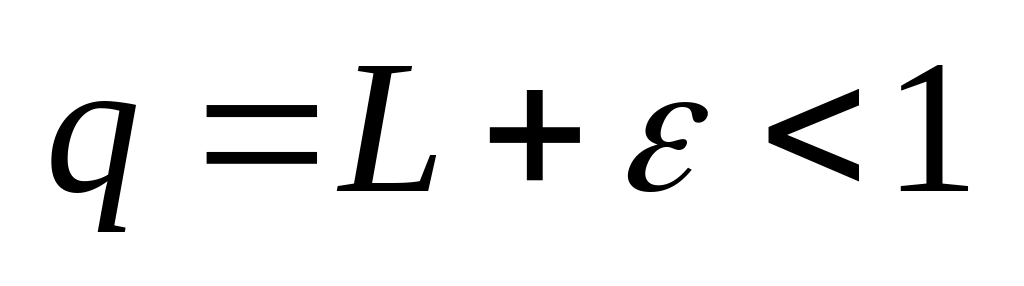
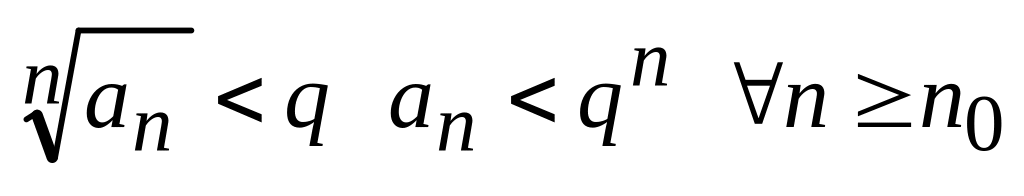
 -
сходится (прогрессия с
-
сходится (прогрессия с
 ),
то
-
сходится по теореме 3.
),
то
-
сходится по теореме 3.Пусть L>1; можно подобрать так, чтобы
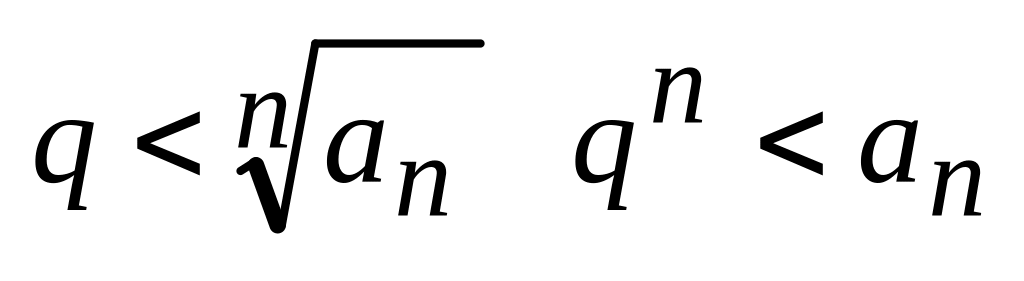 -
расходится, тогда согласно теореме 3
-
расходится.
-
расходится, тогда согласно теореме 3
-
расходится.
§5. Интегральный признак сравнения.
Теорема 2 (интегральный признак сходимости). Пусть - ряд с положительными членами и существует функция f(x) > 0 непрерывная и определенная на интервале [1; + ),
такая что f(n)=an,
![]() .
Ряд
сходится
.
Ряд
сходится
![]() ,
когда сходится
,
когда сходится
![]() .
.
![]() -
ряд Дирихле: при p>1
– ряд сходится;
-
ряд Дирихле: при p>1
– ряд сходится;
при p![]() 1
– ряд расходится.
1
– ряд расходится.
Доказательство.
Для произвольного действительного
числа x найдутся целые
числа k такие, что
![]() .
Так как f(x)
монотонно убывает:
.
Так как f(x)
монотонно убывает:
![]() .
Перейдем к интегралам в неравенстве:
.
Перейдем к интегралам в неравенстве:
![]()
![]() .
.
Просуммируем эти неравенства при всех k=1, .., n.
![]() .
.
Пусть сходится
 ,
где I – число, тогда
,
где I – число, тогда
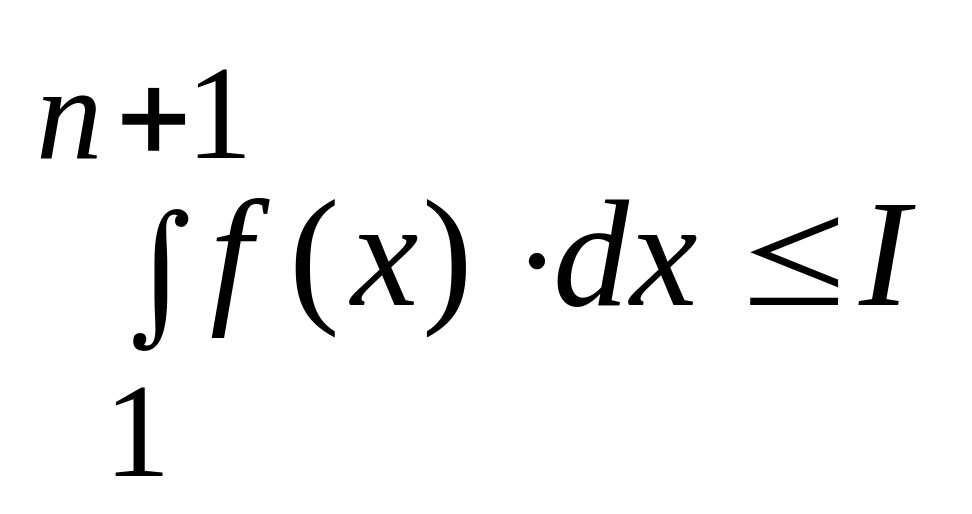 .
Это означает по неравенству (**), что
Sn+1-a1
.
Это означает по неравенству (**), что
Sn+1-a1 I,
т.е.
I,
т.е.
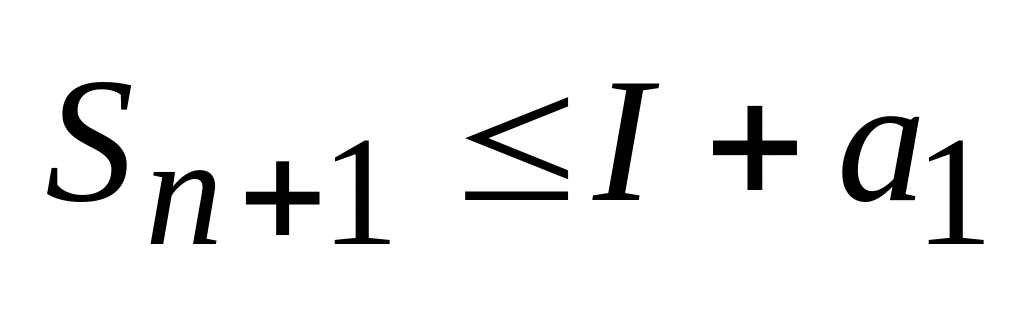 последовательность частичных сумм
ограничена.
последовательность частичных сумм
ограничена.Пусть - сходится, тогда {Sn} – ограничена. Согласно неравенству (*), тогда и последовательность интегралов {
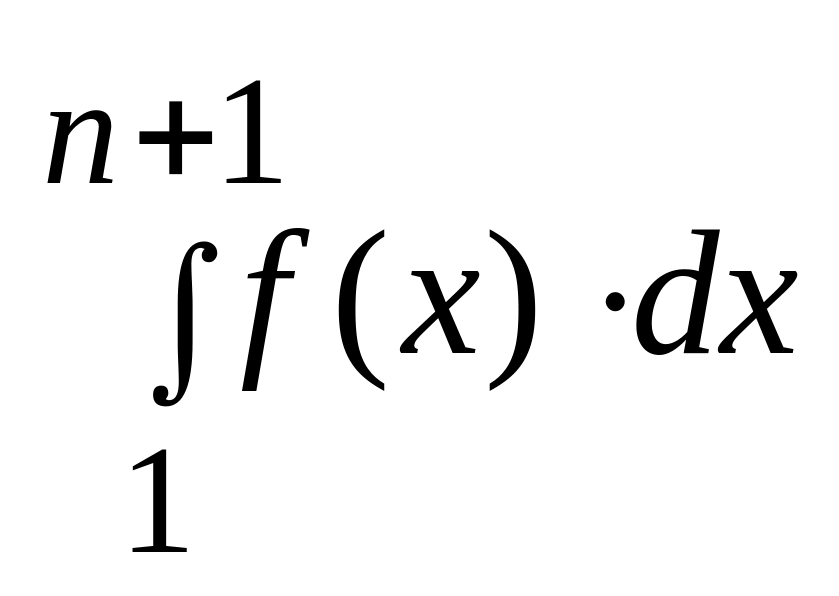 }
– ограничена и значит она сходится при
}
– ограничена и значит она сходится при
 ,
т.е. сходится несобственный интеграл
,
т.е. сходится несобственный интеграл
 - сходится.
- сходится.
Пусть ряд
-
расходится, т.е. расходится последовательность
{Sn}
– (неограниченно возрастает). Тогда
Sn+1-a1
– также неограниченно возрастает. В
силу неравенства (**) последовательность
{![]() }–
}–
неограниченно возрастает. Тогда - расходится.
Если расходится интеграл

 по (*) что
-
расходится.
по (*) что
-
расходится.
q<1 – сход.
q>1- расход.
§6,7. Знакопеременные ряды. Знакочередующиеся ряды. Признак Лейбница.
6. Знакопеременные ряды. Абсолютная и условная сходимость.
Ряд называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные.
Теорема1. Если
знакопеременный ряд
![]() таков, что ряд, составленный из абсолютных
величин его членов
таков, что ряд, составленный из абсолютных
величин его членов
![]() сходится, то и данный знакопеременный
ряд также сходится.
сходится, то и данный знакопеременный
ряд также сходится.
Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов. Если же знакопеременный ряд сходится, а ряд, составленный из абсолютных величин его членов расходится, то данный ряд называется условно или не абсолютно сходящимся рядом.
Знакопеременными называются ряды, которые содержат как положительные, так и отрицательные члены, со сколь угодно большими номерами.
Частным случаем таких рядов являются знакочередующие, т.е. ряды, в которых любые 2 соседних члена имеют разные знаки.
Знакочередующие
ряды удобно представить в виде
![]() (*), где
(*), где![]() (в
случае если a1>0).
(в
случае если a1>0).
Теорема 1 (признак Лейбница). Пусть знакочередующийся ряд (*) удовлетворяет следующим условиям:
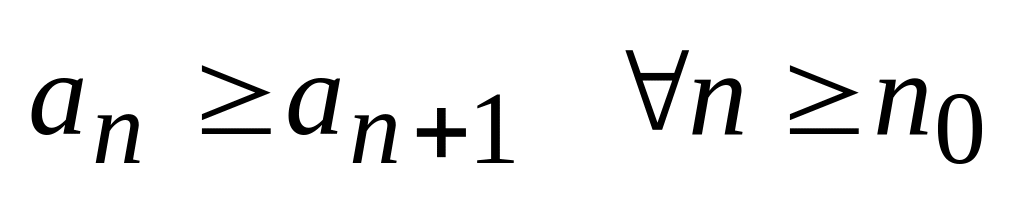 (начиная с номера
n0 монотонно убывает).
(начиная с номера
n0 монотонно убывает). ,
,
тогда данный ряд
сходится, причем для
![]() справедливо следующая оценка остатка
справедливо следующая оценка остатка
![]() .
.
Доказательство. Можно считать, что условие 1 выполняется для всех n. Рассмотрим частичную сумму S2n. Сгруппируем слагаемые следующим образом:
![]()
каждая разность
в скобках неотрицательная. Т.е.
последовательность
![]() и S2n
возрастающая последовательность.
и S2n
возрастающая последовательность.
С другой стороны
последовательность S2n
представима следующим образом
![]() ,
опять в скобках все разности неотрицательны
,
опять в скобках все разности неотрицательны
![]() .
.
Тем самым последовательность {S2n} ограничена и значит она сходится.
Обозначим через
![]() .
.
Рассмотрим
![]() ,
тогда
,
тогда
![]() .
.
Таким образом все
частичные суммы имеют предел S.
Из полученных оценок
![]() ,
поэтому n-ый частичный
остаток
.
,
поэтому n-ый частичный
остаток
.
Пример.
![]() .
.
![]() - убывающая
последовательность
- убывающая
последовательность
![]() ,
значит условие признака Лейбница
выполняется - ряд сходится.
,
значит условие признака Лейбница
выполняется - ряд сходится.
