
- •§1. Числовые ряды.
- •Основные понятия. Примеры.
- •2. Простейшие свойства числовых рядов.
- •§2. Необходимые условия сходимости числового ряда. Гармонический ряд.
- •§3. Признаки сходимости рядов с неотрицательными членами.
- •§4.Признаки д’ Аламбера и Коши сходимости знакоположительных числовых рядов.
- •§5. Интегральный признак сравнения.
- •§6,7. Знакопеременные ряды. Знакочередующиеся ряды. Признак Лейбница.
- •§8. Признаки условной сходимости. Особенности условно сходящихся рядов.
- •§9. Функциональные ряды.
- •2. Равномерная сходимость функциональных рядов.
- •Признак Вейерштрасса.
- •4. Свойства равномерно сходящихся рядов.
- •§10. Степенные ряды.
- •2. Свойства степенных рядов.
- •§11. Ряды Тейлора.
- •§12. Разложение функций в ряд Тейлора (Маклорена).
- •§1. Числовые ряды.
Ряды.
§1. Числовые ряды.
Основные понятия. Примеры.
Определение:
Пусть {an}
– числовая последовательность. Выражение
a1+a2+…+a3+…=![]() называется числовым рядом. Числа
а1, а2, …- члены
ряда, причем an
– общий член ряда. Сумма
Sn=a1+a2+…+a3=
называется числовым рядом. Числа
а1, а2, …- члены
ряда, причем an
– общий член ряда. Сумма
Sn=a1+a2+…+a3=![]() называется
n-ой частичной
суммой данного ряда (сумма первых
n членов ряда).
называется
n-ой частичной
суммой данного ряда (сумма первых
n членов ряда).
Определение:
Если существует конечный предел
последовательности {Sn}
равный S, то ряд
называется сходящимся, а число
S – его суммой.
![]() .
.
Если же такого
предела не существует, либо он равен
![]() ,
то ряд называется расходящимся.
,
то ряд называется расходящимся.
Предложение:
Ряд
![]() -
сходится
-
сходится
![]() ,
,![]() (последовательность остатков
(последовательность остатков
![]() 0).
0).
Доказательство.
Из равенства 1 можно представить
rn=S-Sn,
тогда
![]()
2. Простейшие свойства числовых рядов.
1.Перестановка, отбрасывание или добавление конечного числа членов ряда не влияет на его сходимость или расходимость.
2.Пусть ряд
![]() и ряд
и ряд
![]() -
сходится, тогда сумма этих рядов
-
сходится, тогда сумма этих рядов
![]() тоже сходится.
тоже сходится.
Доказательство.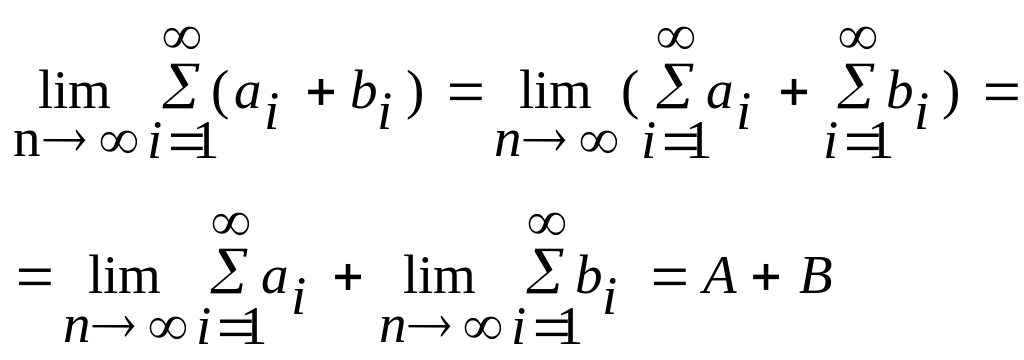 - предел существует.
- предел существует.
1.Если ряд
![]() - сходится, то и ряд
- сходится, то и ряд
![]() -сходится, где c -
некоторое число. Что всякая линейная
комбинация сходящихся рядов есть
сходящийся ряд.
-сходится, где c -
некоторое число. Что всякая линейная
комбинация сходящихся рядов есть
сходящийся ряд.
§2. Необходимые условия сходимости числового ряда. Гармонический ряд.
Теорема 1
(необходимый признак сходимости). Если
ряд
![]() -
сходится, то общий член ряда → 0 (
-
сходится, то общий член ряда → 0 (![]() ).
).
Доказательство.
Между частичными суммами существует
следующая связь: Sn=Sn-1+an,
и поэтому
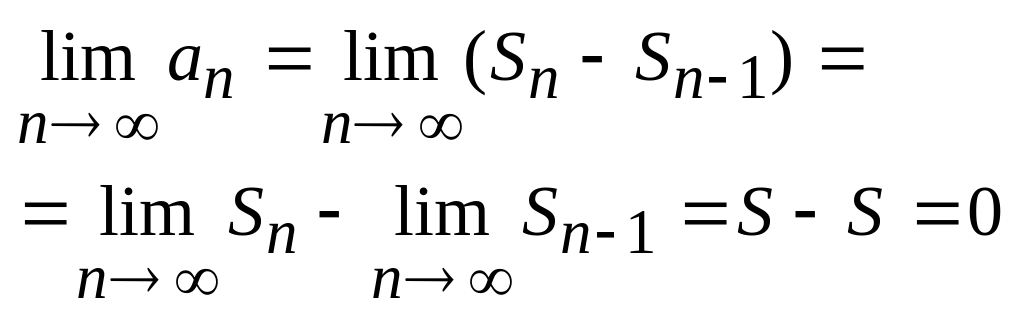 .
.
Следствие:
(достаточный признак расходимости).
Если
![]() ,
то ряд расходится.
,
то ряд расходится.
Пример1.
![]() -гармонический
ряд.
-гармонический
ряд.
![]() →
ряд расходится.
→
ряд расходится.
§3. Признаки сходимости рядов с неотрицательными членами.
Общий вид:
,
![]() .
.
Теорема 1
(предельный признак сравнения). Пусть
и
![]() с
положительными членами. Если существует
с
положительными членами. Если существует
![]() ,
который
,
который
![]() и
и
![]() ,
тогда ряды
и
сходятся или расходятся одновременно.
,
тогда ряды
и
сходятся или расходятся одновременно.
Доказательство.
Обозначим
![]() ;
;
![]() .
Согласно определению обозначим все
члены последовательности {
.
Согласно определению обозначим все
члены последовательности {![]() }
начиная с некоторого номера находящегося
сколь угодно близко к L,
т.е.
}
начиная с некоторого номера находящегося
сколь угодно близко к L,
т.е.
![]() существует номер
существует номер
![]() такой, что
такой, что
![]() .
.
Умножим все части неравенства на bn (bn>0), получим следующее:
![]() .
.
1.Пусть сходится
ряд
,
тогда сходится
![]() и тогда согласно теореме 3 ввиду
неравенства (**) сходится ряд
.
и тогда согласно теореме 3 ввиду
неравенства (**) сходится ряд
.
2.Пусть сходится
ряд
,
тогда согласно теореме 3 ввиду неравенства
(**) сходится ряд
![]() из
чего следует сходимость
.
из
чего следует сходимость
.
Аналогично доказывается случай расходимости.
Замечание.
Применяя признак сходимости чаще
всего сравнивают с
![]() и
и
![]() .
.
Теорема 2
(признак сравнения). Пусть
имеется два ряда
и
и
существует номер n0
![]() N такой, что выполняется
следующее неравенство
N такой, что выполняется
следующее неравенство
![]() ,
тогда:
,
тогда:
если ряд - сходится - сходится.
если ряд - расходится - расходится.
Доказательство.
Можно считать, что члены второго ряда
![]() членам первого ряда уже начиная с первого
номера (иначе можно рассматривать
остатки ряда; их сходимость и расходимость
равносильна сходимости или расходимости
рядов). Считаем, что неравенства
членам первого ряда уже начиная с первого
номера (иначе можно рассматривать
остатки ряда; их сходимость и расходимость
равносильна сходимости или расходимости
рядов). Считаем, что неравенства
![]() выполняется для
выполняется для
![]() ,
тогда аналогичное неравенство выполняется
и для {Sn},
т.е.
,
тогда аналогичное неравенство выполняется
и для {Sn},
т.е.
![]() .
.
Пусть - сходится, тогда последовательность {
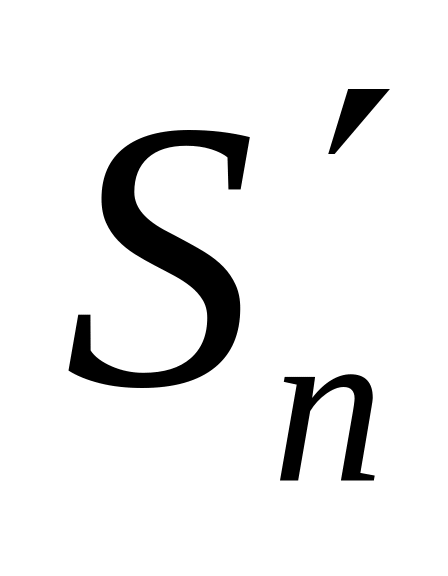 }-
ограничена, значит ограничена и
последовательность {Sn}
-
сходится.
}-
ограничена, значит ограничена и
последовательность {Sn}
-
сходится.Пусть - расходится. Это означает, что неограниченна его последовательность частичных сумм Sn = {
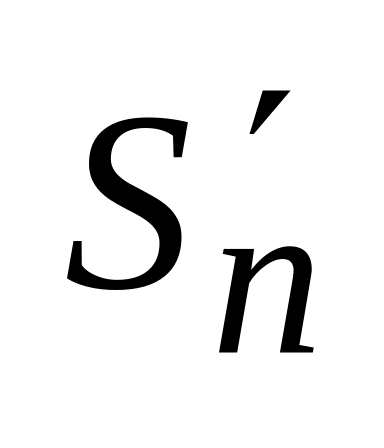 }
– неограниченна, значит расходится
.
}
– неограниченна, значит расходится
.
