21. Графический метод проверки стандартных предположений регрессионного анализа.

Существует четыре стандартных предположения о процессе порождения данных. Первое из этих предположений (в модели не все значения x₁, х₂, …, х_n совпадают между собой) проверяется перед построением регрессионной модели. Остальные три можно проверить только тогда, когда уравнение регрессии уже составлено. Без соблюдения этих условий построенная модель теряет смысл.

Оцененная модель проверяется на отсутствие автокорреляционной зависимости остатков от номера наблюдения, на независимость случайных ошибок ε₁, ε₂,..., ε_n, математическое ожидание которых должно стремиться к нулю (Mε_i=0), на постоянство или гомоскедастичность дисперсии ошибок [ ]. Анализ соблюдения перечисленных условий (дисперсионный анализ), проводят, используя графики стандартизированных остатков

(2.42)

где - оценка дисперсии остатков

(2.43)

Графики позволяют выявлять типичные отклонения от стандартных предположений о модели наблюдений по характеру поведения остатков. При большом количестве наблюдений поведение стандартизированных остатков имитирует поведение ошибок .

Наиболее часто используют графики зависимости стандартизированных остатков (как ординат) от

- оцененных значений у (по оси абсцисс);

- отдельных объясняющих переменных;

- номера наблюдения, если наблюдения производятся в последовательные моменты времени равными интервалами.

График зависимости от , позволяет выявить три довольно распространенных нарушения стандартных предположений о модели наблюдений:

1. Выделяющиеся наблюдения - наличие отдельных наблюдений, для которых либо математическое ожи­дание ошибок отлично от нуля , либо дисперсия ошибки существенно превышает величину дисперсий остальных ошибок. Подобные наблюдения могут обнаруживать себя на графике, как наблюдения со слишком большими по величине остатками (рис. 2.4).

Рисунок 2.5

2. Неоднородность дисперсии (гетероскедастичность), например, в форме той или иной функциональной зависимости 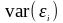от величины . Если рассматриваемый график имеет вид, изображенный на рис. 2.4, то это скорее всего отражает рост дисперсий ошибок с ростом значений .

Рисунок 2.6

3. Неправильная спецификация модели в отношении множества объясняющих переменных, приводящих к нарушению условия (рис. 2.5).

Рисунок 2.7

График, зависимости от значений j-й объясняющей переменной помогает выявить нелинейную зависимость у от j-й объясняющей переменной в случае множественной регрессионной модели (рис. 2.6, 2.7).

Рисунок 2.8

Рисунок 2.9

График зависимости остатков от номера наблюдения полезен в случае, когда наблюдения производятся последовательно во времени (через равные интервалы времени). По такому графику можно обнаружить:

1. Изменение дисперсии ошибок с течение времени.

Рисунок 2.10

2. Не включение в модель переменных, зависящих от времени и существенно влияющих на объясняемую переменную.

Рисунок 2.11

3. Не выполнение условия независимости в совокупности случайных ошибок в форме их автокоррелированности (определенной функциональной за­висимости). График остатков в случае положительной автокоррелированности приведен на рис. 2.12 и в случае отрицательной – на рис. 2.13.

Рисунок 2.13 Рисунок 2.13

В первом случае проявляется тенденция сохранения знака остатка при переходе к следующему наблюдению (за положительным остатком скорее следует также положительный остаток, а за отрицательным – отрицательный). Во втором случае проявляется тенденция смены знака остатка при переходе к следующему наблюдению (за положительным остатком скорее следует отрицательный остаток, а за отрицательным – положительный).

Помимо графических существует довольно много процедур, предназначенных для проверки стандартных предположений о линейной модели наблюдений, использующих статистические критерии.