39. Метод взвешенных наименьших квадратов (обобщенный мнк)

Данный метод применяется, когда построенная модель множественной регрессии не отвечает требованию гомоскедастичности возмущений. Найденные параметры такой модели не обладают свойствами несмещенности и эффективности, о чем можно судить по гетероскедастичности остатков. От таких нежелательных свойств модели можно избавиться с помощью следующих преобразований.

Согласно обобщенного (взвешенного) МНК оценки параметров определяются из условия минимума суммы взвешенных квадратов ошибок:

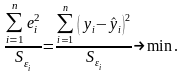(4.36)

Если полученное после оценки параметров модели обычным МНК уравнение имеет вид

(4.37)

то чтобы избавиться от нежелательных свойств ошибок его делят на оценку стандартного отклонения ошибок.

(4.38)

Такая модель будет гомоскедастичной и для ее оценивания можно применить обычный МНК.

Осуществленное преобразование приводит к модификации критерия метода наименьших квадратов. Теперь ошибки (остатки) модели не просто складываются, а берутся с «весами», причем наблюдениям с меньшими дисперсиями (более точным) придаются большие веса. Это позволяет получить эффективные, несмещенные оценки параметров модели. Обобщенный МНК для моделей с гетероскедастичностью называют методом взвешенных наименьших квадратов. Данный метод может применяться и для моделей с автокоррелированными остатками

40. Понятие и примеры фиктивных переменных

Зачастую в регрессионных моделях в качестве объясняющих пе­ременных приходится использовать не только количественные (опре­деляемые численно), но и качественные переменные. Например, спрос на некоторое благо может определяться ценой данного благо, пеной на заменители данного блага, ценой дополняющих благ, доходом по­требителей и т. д. (эти показатели определяются количественно). Но спрос может также зависеть от вкусов потребителей, их ожиданий, национальных и религиозных особенностей и т. д. А эти показатели представить в численном виде нельзя. Возникает проблема отражения в модели влияния таких переменных на исследуемую величину. Это достаточно сложная задача.

Обычно в моделях влияние качественного фактора выражается в виде фиктивной (искусственной) переменной, которая отражает два противоположных состояния качественного фактора. Например, «фактор действует» – «фактор не действует», «курс валюты фиксированный» – «курс валюты плавающий», «сезон летний» – «сезон зимний» и т. д. В этом случае фиктивная переменная может выражаться в двоичной форме:

В зависимости от целей исследования используются различные фиктивные переменные:

Переменная d называется фиктивной (искусственной, двоичной) переменной (индикатором).

Таким образом, кроме моделей, содержащих только количест­венные объясняющие переменные (обозначаемые x_i), в регрессион­ном анализе рассматриваются также модели, содержащие лишь каче­ственные переменные (обозначаемые d_i), либо и те и другие одновре­менно. Искусственные переменные могут входить в состав регрессионных моделей в качестве как объясняющих, так и объясняемых переменных.

Методы оценки параметров и качества моделей, содержащих фиктивные переменные, аналогичны рассмотренным ранее методам для моделей, содержащих только количественные переменные. Рассмотрим примеры простейших моделей с фиктивными переменными.