Обратно пропорциональная зависимость, Линеаризация этой модели и ее эластичность
Если у – объем плановых инвестиций, a z – норма банковского процента, то между ними существует связь (рис. 3.2), которая часто выражается в форме обратно пропорциональной зависимости:
.
(3.12)
Эта модель приводится к линейной, заменой
переменной
:
.
Рисунок 3.2
В этой модели эластичность у по z отрицательна и меньше единицы по абсолютной величине
(3.13)
следовательно объем плановых инвестиций неэластичен по отношению к норме процента (проценты растут быстрее, чем инвестиции).
В моделях «доход-потребление», относящихся
к потреблению продуктов питания линейная
модель в логарифмах уровней, выражающая
уменьшение нормы потребления
с ростом доходов х, не всегда
удовлетворительна, поскольку эластичность
в такой модели
.
0
Модели с убывающей эластичностью, их линеаризация
Часто более подходящей является модель связи с убывающей эластичностью (рис. 3.3). Например:
(3.14)
Тогда
;
(3.15)
(3.16)
Рисунок 3.3
В этой модели возникают проблемы с отрицательными значениями у при малых значениях z.
Такого недостатка нет в модели
,
(3.17)
то есть
.
(3.18)
Здесь
,
.
(3.19)
П
оследнее
соотношение выражает закон Энгеля
– убывания эластичности потребления
продуктов питания по доходу. Значения
у в этой модели ограничены сверху
значением
.
Рисунок 3.4
Модели 3.14 и 3.17 сводятся к линейной форме путем перехода от уровней переменных к их логарифмам или обратным величинам.
Итерационные методы подбора нелинейных моделей
Если, исследователь принимает модель наблюдений
,
(3.20)
то тем самым он соглашается с видом модели
или
,
(3.21)
то есть соглашается с мультипликативным
вхождением ошибок
в нелинейное уравнение
.
Однако не исключено, что по существу модель должна иметь вид
,
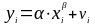(3.22)
то есть имеет аддитивные ошибки.
В этой модели взятие логарифмов от обеих частей не приводит к линейной модели наблюдений.
Для получения оценок наименьших квадратов
параметров
и
сумму квадратов
(3.23)
минимизируют, используя итерационные
методы, в процессе реализации которых,
сначала задаются некоторые «стартовые
значения» оцениваемых параметров, а
затем производится последовательное
приближение значений (а и b)
оценок параметров
и
,
минимизирующих
(a,
b).