1 Поняття про числовий ряд і його суму. Геометричний ряд.

Нехай задано числову послідовність . Тоді вираз 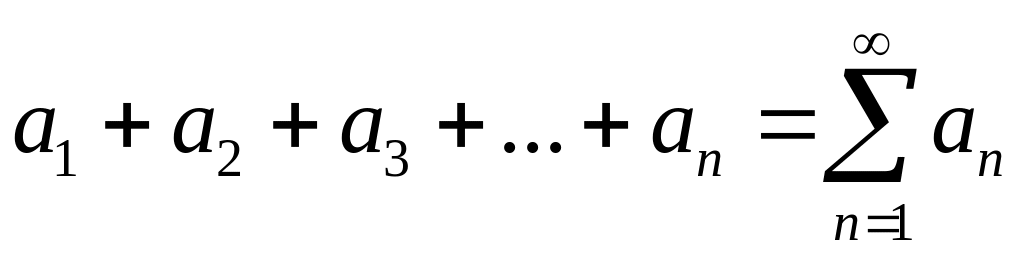називається числовим рядом; елементи послідовності − членами ряду; елемент − -м членом ряду; суму − частинною сумою ряду.

Числовий ряд називається збіжним, якщо послідовність частинних сум збігається до деякого числа , що називається сумою ряду:

Якщо не існує скінченої границі послідовності, то ряд називається розбіжним.

Нехай , тоді такий числовий ряд називається геометричним рядом. В цьому випадку отримаємо такі частинні суми: 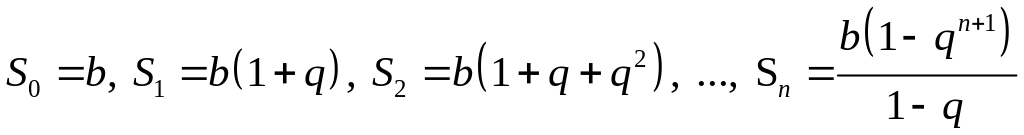. Спрямуємо та розглянемо два випадки: та . В результаті чого отримаємо в першому випадку 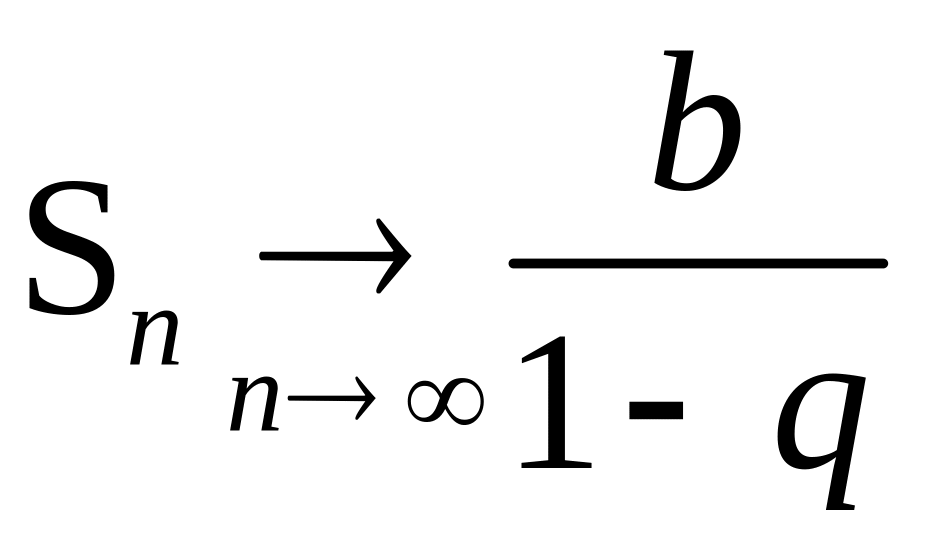, а в другому випадку скінченої границі не існує, ряд є розбіжним.

2 Необхідна умова збіжності ряду. Гармонічний ряд. Залишок ряду. Властивості збіжних рядів. Критерій Коші збіжності ряду.

Нехай маємо ряд , тоді , де та . У збіжних рядів загальний член ряду завжди прямує до нуля при . Це називається необхідною умовою збіжності. Відповідно можна стверджувати, що коли загальний член ряду не прямує до нуля ряд є розбіжним. Це називається достатньою ознакою розбіжності.

Ряд вигляду називається гармонічним. Таким чином маємо 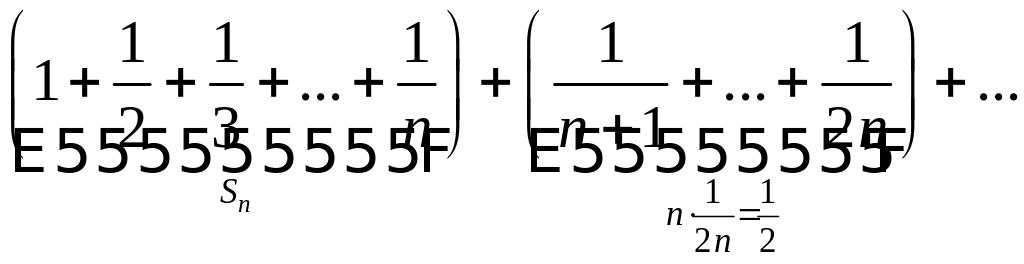в результаті чого залишок суми ряду завжди більший за , а отже у відповідності до критерію Коші ряд є розбіжним. Ряд вигляду називається узагальненим гармонічним.

Будь-який ряд можна записати у вигляді 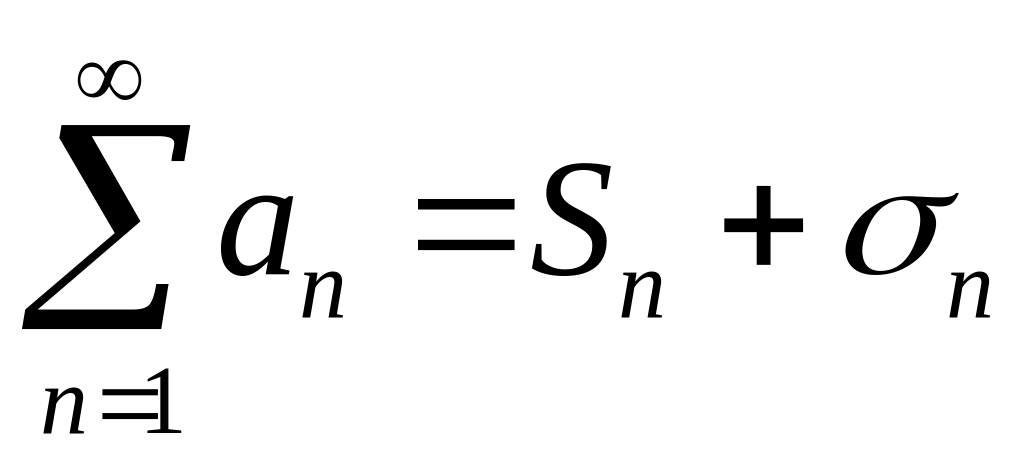, де , при цьому величина називається залишком (хвостом) ряду.

Властивості збіжних рядів:

• Якщо , то

• Якщо і , то

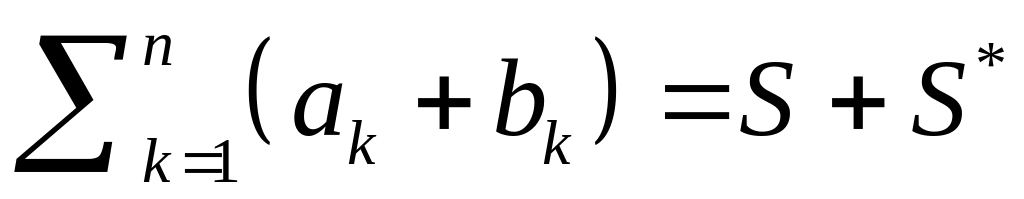
• , де та . Це є необхідною умовою збіжності.

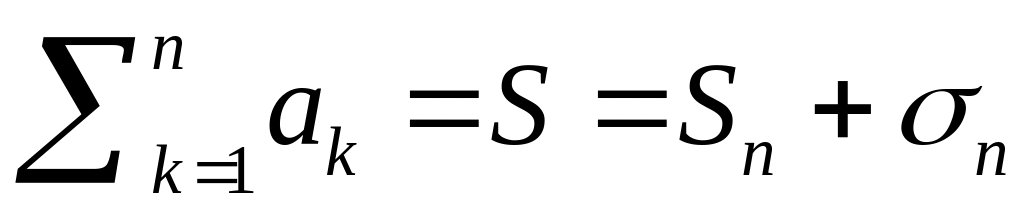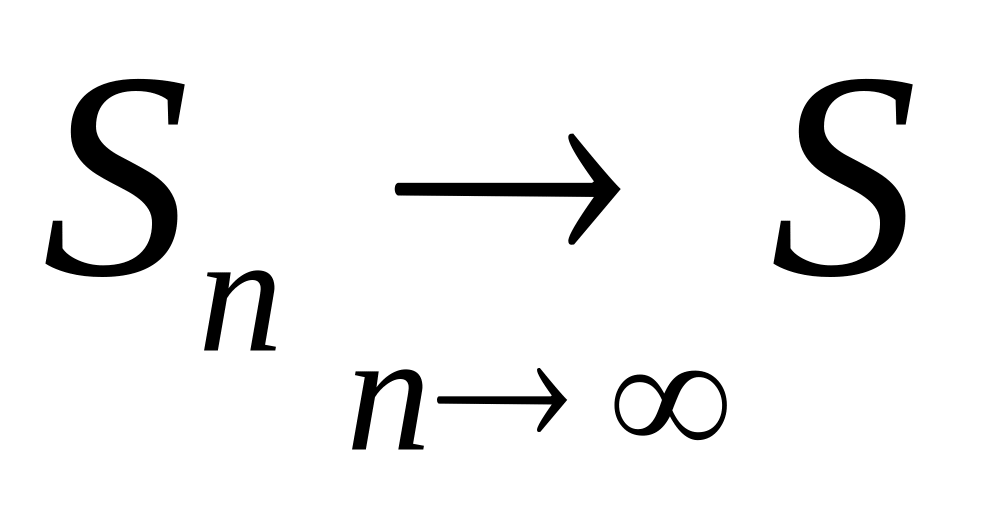• , де та .

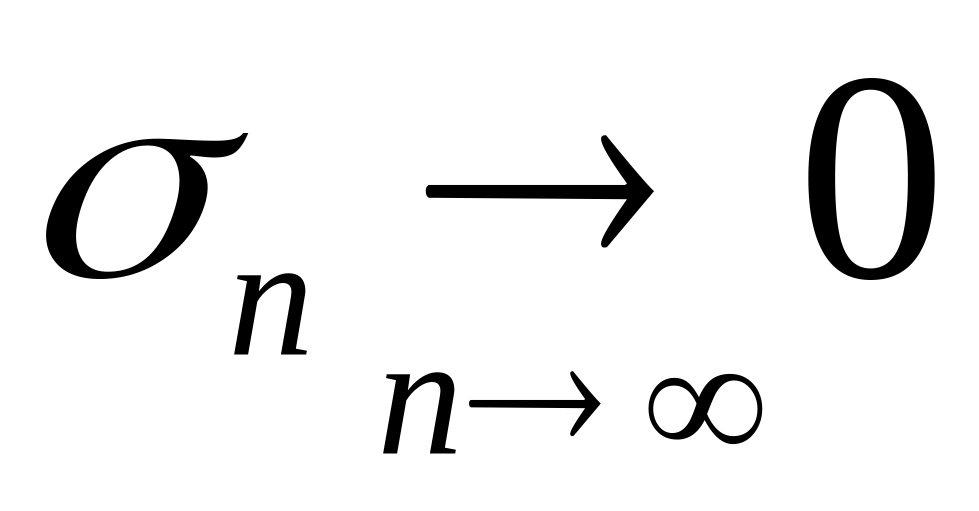Критерій Коші: Ряд є збіжним лише тоді, коли для довільного знайдеться таке залежне від , що для довільного , виконується рівність

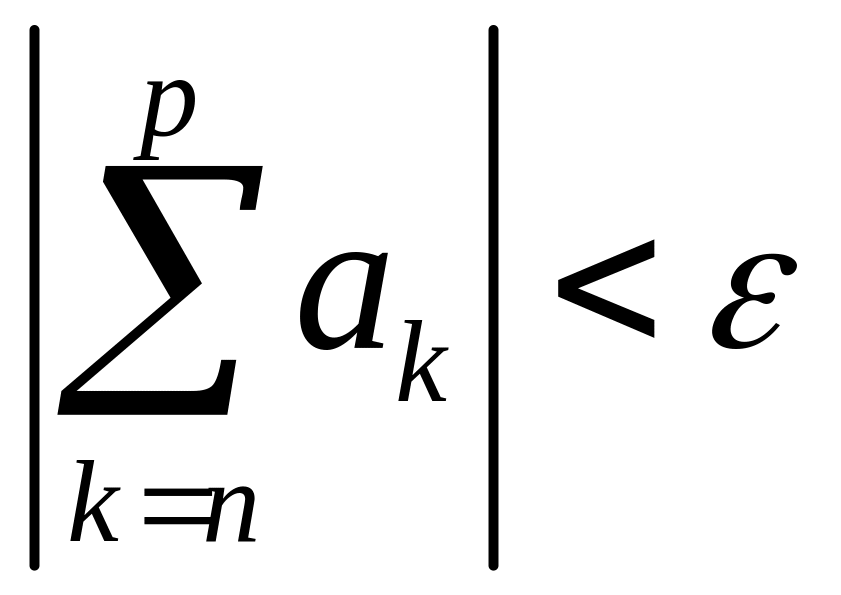
Символами:

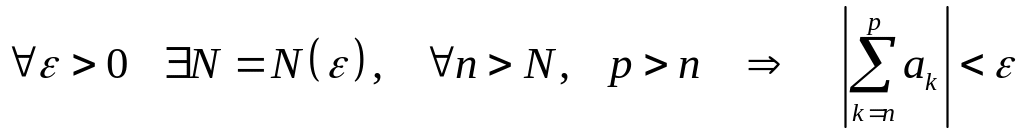
3 Ознаки збіжності числових рядів з додатними членами

1. Перша ознака порівняння.

Нехай маємо ряди 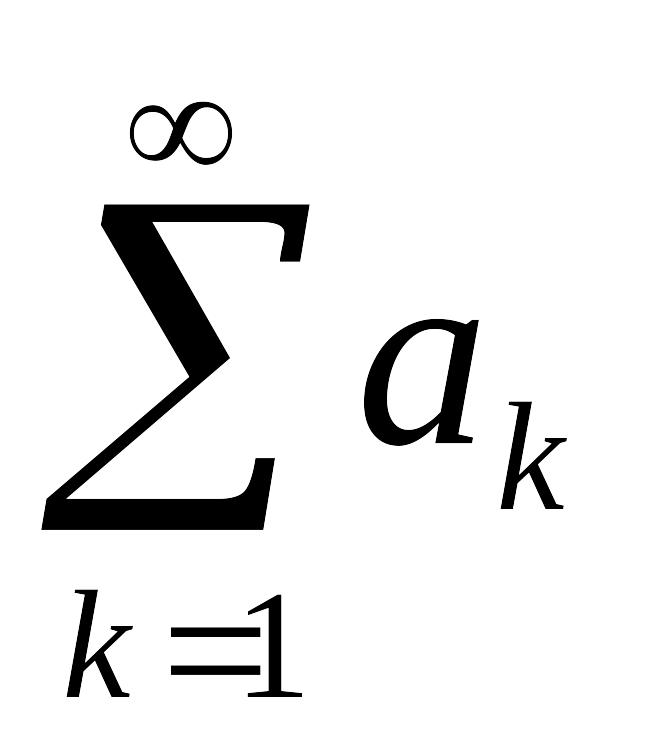та , при цьому для всіх значень виконується нерівність , тоді:

• із збіжності першого ряду випливає збіжність другого ряду.

• із розбіжності другого ряду випливає розбіжність першого ряду.

2. Гранична ознака порівняння.

Нехай для членів рядів та існує скінченна границя , причому . Тоді ці ряди збігаються або розбігаються одночасно.

Доведення: (доведемо, що, якщо другий ряд розбігається, то перший також розбігається):

Для будь-якого знайдеться такий номер починаючи з якого , де . Таким чином . Отже відповідний „хвіст” першого ряду більший за хвіст другого ряду помноженого на . Оскільки відповідно до критерію Коші „хвіст” другого ряду не прямує до нуля, то не прямує до нуля і „хвіст” першого ряду, що свідчить про його розбіжність.

3. Ознака Д’Аламбера.

Якщо для ряду , існує границя , то при - ряд розбіжний; при - ряд збіжний; при - ряд вимагає дослідження за допомогою інших ознак.

4. Радикальна ознака Коші.

Якщо для ряду існує границя , то при - ряд розбіжний, при - ряд збіжний і при - ряд потребує подальшого дослідження іншим методом.

Доведемо, що ряд збіжний при .

Для будь-якого , існує таке , що при , звідси виходить, що

, що й треба було довести

5. Інтегральна ознака Коші.

Таким чином, якщо ряд збіжний, то збіжним є і невласний інтеграл

Отже, розглянутий вище ряд та невласний інтеграл першого роду збіжні чи розбіжні одночасно.