38. Елементи класифікації задач стохастичного програмування. Приклади задач стохастичного програмування.

Типову задачу математичного програмування в детермінованій постановці формулюють так: визначити вектор 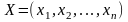, для компонент якого:

,

,

.

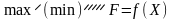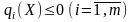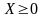Якщо функції в даній задачі крім керованих параметрів Х залежать ще і від деяких випадкових величин , то маємо задачу стохастичного програмування:

,

,

, ,

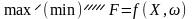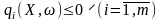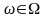де Ω — простір подій ω.

Залежно від можливості отримати та врахувати інформацію стосовно детермінованості (стохастичності) функцій 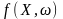, 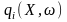постановки задач СП можуть містити:

1. стохастичні коефіцієнти цільової функції та детерміновані обмеження;

2. детерміновані коефіцієнти цільової функції та стохастичні вільні члени і коефіцієнти системи обмежень;

3. стохастичні коефіцієнти цільової функції, вільні члени і коефіцієнти системи обмежень.

Конкретні постановки задач СП мають свою специфіку. Передусім необхідно визначити:

1. Детермінованим чи випадковим є вектор Х. Якщо вектор Х є детермінованим, то він не залежить від випадкових параметрів моделі. Якщо ж він випадковий, то тоді Х є функцією від ω — 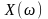, тобто залежить від випадкових змінних.

2. Як розуміти максимізацію (мінімізацію) цільової функції — як абсолютну (для всіх значень ) чи як максимізацію її математичного сподівання або деякої іншої ймовірнісної характеристики цієї функції (моди, медіани), або як мінімізацію середнього квадратичного відхилення?

3. Як виконуються обмеження: абсолютно для всіх чи в середньому, або з допустимими порушеннями, ймовірність яких мала?

При постановці задач стохастичного програмування необхідно виходити не лише з математичних міркувань, а й з економічного зміст.

Методи розв’язування стохастичних задач поділяють на дві групи — прямі та непрямі.

Прямі методи використовують для розв’язування задач стохастичного програмування, коли існують способи побудови функцій і 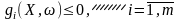на базі інформації щодо параметра ω. Непрямими є методи зведення стохастичної задачі до ЗЛП чи ЗНП, тобто перехід до детермінованого аналога задачі стохастичного програмування.

39. Одноетапні статичні задачі управління виробництвом за умов ризику.

Під статичними розуміють такі моделями, всі параметри яких протягом всього періоду управління залишаться незмінними або ж їх зміною можна знехтувати. Вивчення статичних моделей є доцільним, якщо необхідно встановити початковий рівень виробництва нових товарів, що є відправним етапом для подальшого розв’язку динамічних задач управління виробництвом. В однокрокових задачах нехтують також динамікою надходження інформації, рішення приймаються на основі інформації, яка існує на момент прийняття рішення на початку інтервалу (періоду) управління (планування). Рішення за цих умов є детермінованим. Розглянемо виробничо-економічну систему з певною потужністю х, попит на які на ринку (у споживача) заздалегідь не відомий і вважається випадковою величиною Cо є О,. Позначимо через q(x) величину загальних витрат при виробництві продукції, а через f(x, Cо) збитки, яких зазнає виробництво від недовипуску продукції, якщо Cо>х, через/^х, Cо) — збитки, що виникають тоді, коли виробництво перевищує величину випадкового попиту, тобто коли х>Cо. Таким чином, задача полягає у знаходженні такої кількості товару х, який мінімізує сумарні сподівані витрати, що складаються із вартості виробництва, тобто F(x) = q(x) + Mf(x,Co) —> min(1) при обмеженнях хє X ,(2) де X — деяка множина я-мірного простору, яка може бути утворена обмеженням, пов’язаним з потужністю підприємства, обсягами продукції. У разі якщо максимізується прибуток від реалізації продукції, яка виробляється. F(x) = q(x) - Mf(x, Co) —> max. Типові труднощі, які виникають при розв’язуванні однокро-кової задачі (1), (2), полягають у складності (або неможливості) точного обчислення значень функції сподіваних витрат F(x) та її градієнта, що пов’язано з обчисленням інтегралу виду F(x) = q(x) + f(x, CO)d(p{co) з n де (p(co) — функція розподілу випадкового параметру.