24. Функція ризику

Функція ризику визначається як лінійне перетворення позитивно чи негативно заданого інгредієнта ФО до відносних одиниць вимірювання. Таке перетворення встановлює порядок відліку ФО для кожного стану ЕС :

1) для , коли мають зафіксований стан економічного середовища , знаходять величину і функція ризику визначається у вигляді: ;

2) для F=F ^— при фіксованому знаходять

i функція ризику визначається як .

25. Критерій першої інформаційної ситуації

Під інформаційною ситуацією (ІС) з погляду суб’єкта керування (залежно від ступеня його інформованості) розуміють певний ступінь градації невизначеності вибору середовищем своїх станів у момент прийняття рішення.

І₁ — перша ІС. Характеризується заданим розподілом апріорних імовірностей на елементах множин  (достатня за обсягом інформація):

P = {p₁; p₂; …; p_n}; p_j = P( = _j); ,

Розглянемо деякі з основних критеріїв прийняття рішень, що можуть використовуватись у полі цієї інформаційної ситуації:

1. Критерій Байєса:

Згідно з критерієм Байєса у випадку, коли F = F⁺, оптимальним рішенням вважається таке, для якого математичне сподівання відповідного вектора оцінювання досягає найбільшого можливого значення, тобто знаходять, виходячи з умови:

:^*) В⁺( ; Р) = В⁺(х_k; Р),де В⁺(х_k; Р) = = М(F ).

Якщо ж F = F^–, то оптимальне рішення визначається, виходячи з умови:

: ( ; Р) = (х_k; Р), де (х_k; Р) = = М( ).

2) Модальний критерій

У випадку, коли оптимальне рішення відшукується з умови:

,

У випадку, коли

.

3)Критерій мінімальної дисперсії

У випадку, коли ⁺ чи , оптимальне рішення задовольняє умову:

: ( ; Р) = ( ; Р),

26. Критерії четвертої інформаційної ситуації

Ситуація I4 характеризується відсутністю в об'єкта управління інформації про розподіл ймовірностей вибору середовищем своїх станів. На практиці такі ситуації зустрічаються при реалізації нових зразків товарів народного споживання, коли цілком невідомий попит, коли на підприємстві впроваджуються нові зразки техніки, нові технології, транспортні маршрути і т.д.

Критерій Бернулі - Лапласа.

У основу критерію покладений «принцип недостатньої підстави», що сформулював Бернулі. Відповідно до цього принципу вважають, що ймовірності вибору середовищем своїх станів рівні

,

Такі оцінки розподілу апріорних ймовірностей дозволяють застосовувати критерії першої інформаційної ситуації I1 . Тоді, оптимальним відповідно до критерію Бернулі - Лапласа буде рішення , X_ko є X, що задовольняє умові

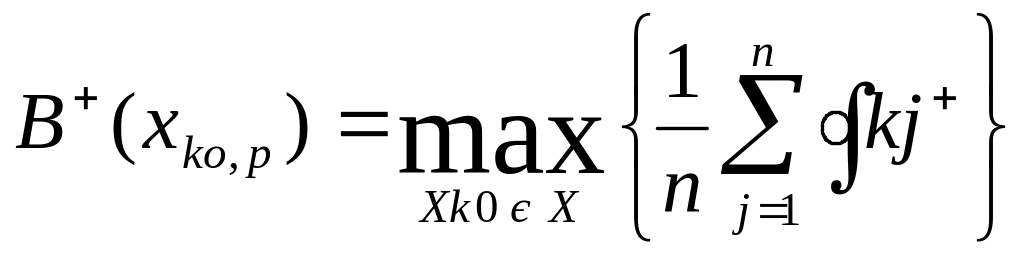
Критерій Хоменюка.

Розглянемо ситуацію прийняття рішень для функціонала заданого у формі F⁺ і F^- .

Критерій Хоменюка базується на понятті «потенційного розподілу ймовірностей» на множині станів середовища Q . Потенціальний вектор pˆ апріорних ймовірностей вибору середовищем своїх станів для

F = F ⁺ визначається по формулі:

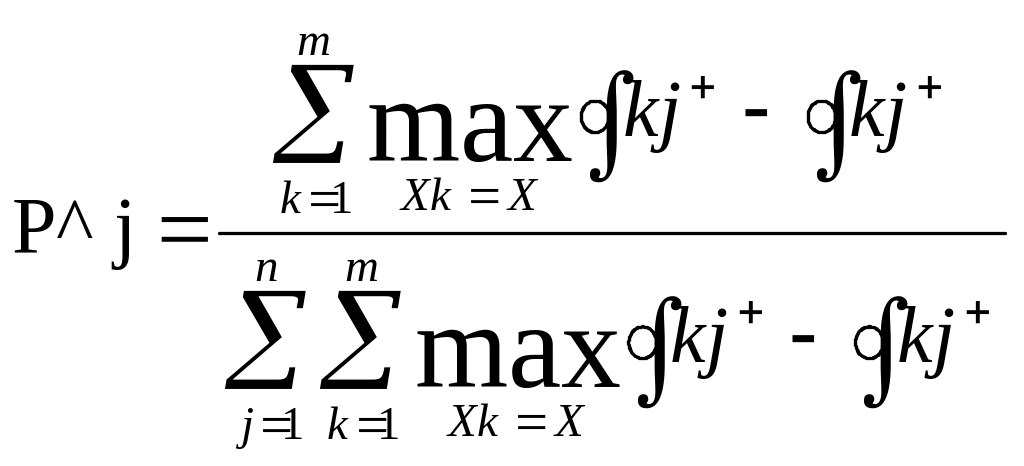
а для F = F^-

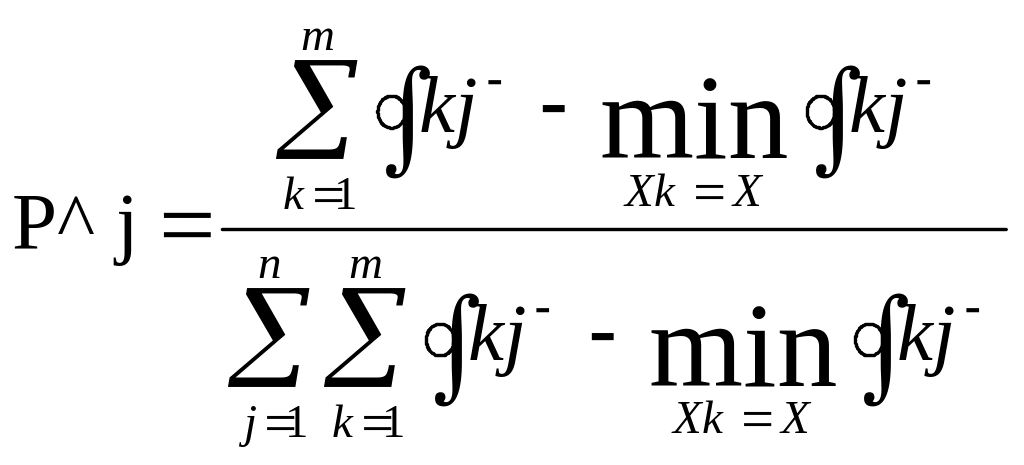
Принцип потенціального розподілу ймовірностей базується на тому, що середовище віддає перевагу вибору із більшою ймовірністю (із меншою ймовірністю F = F^- для ) такого стану середовища з множини Θ, на якому внесок у сумарне значення оцінного F⁺ функціонала по всіх xk є X рішеннях і станам із Θ , має менший розмір у порівнянні з іншими аналогічними значеннями.

Такий принцип представляє собою для суб’єкта управління цілком реальну модель поводження середовища, що прагне в середньому понизити значення оцінного функціонала F⁺ (або підвищити у випадку F = F^- ) для ухвалення рішення. Після одержання оцінок pˆj апріорних ймовірностей pj , проблема ухвалення рішення зводиться до першої інформаційної ситуації I1.

27. Критерії п’ятої інформаційної ситуації

На відміну від пасивних середовищ і середовищ із заданим розподілом ймовірностей, - активне середовище прагне до вибору таких станів із множини , для яких функціонал оцінювання F F⁺приймає мінімальне значення з множини своїх можливих значень.

У теоретичній моделі ступінь невизначеності зменшена за рахунок допущення, що економічне

середовище активно протидіє досягненню найбільшої ефективності прийнятих рішень шляхом вибору таких своїх станів, що обумовлять мінімальну максимальну ефективність процесу управління.

Критерій Вальда.

Основною ціллю об'єкта управління в даній ситуації є забезпечення собі гарантованих (максимальних) рівнів значень функціонала оцінювання. Тоді, при F F^, відповідно до принципу максиміну кожному рішенню присвоюють x k  X показник його гарантованого рівня:

Оптимальним вважають таке рішення x_ko X , для якого відповідний показник максимальний:

тобто оптимальним є рішення, що призводить до найкращого з найгірших значень оцінного функціонала.

Критерій Сэвіджа.

Критерій Севіджа використовують коли F F^.

Цей критерій рекомендує в умовах невизначеності вибрати ту стратегію, при якому розмір ризику приймає найменше значення в самій несприятливій ситуації (задовольняє принципу мінімакса).

Таким чином, у відповідності F F^з цим критерієм оптимальним рішенням є рішення Xk0 , що задовольняє умові:

Критерії Сэвіджа і Вальда - це критерії крайнього песимізму

28. Критерії шостої інформаційної ситуації

Дана інформаційна ситуація визначається наявністю чинників, що характеризують два типи «проміжного» стану поводження середовища. Для першого типу характерно наявність в органа управління деякої «неясної» інформації про істинні розподіли ймовірностей вибору середовищем своїх станів із множини .

Для другого типу передбачається, що орган управління має інформацію про можливі стани середовища, що є «проміжної» між I1 ситуаціями I5 і , що характеризується, з одного боку, повним або частковим знанням розподілів ймовірностей на , а з іншого боку - антагоністичним поводженням середовища.

Критерій Гурвіца.

Відмінною рисою критерію є те, що в ньому передбачається не повний антагонізм середовища, як у критеріях Вальда і Севиджа, а лише частковий (тобто рекомендується керуватися легковажним оптимізмом).

Сутність критерію Гурвіца полягає в знаходженні оптимального рішення xk0 (або множини таких рішень), для якого виконується умова:

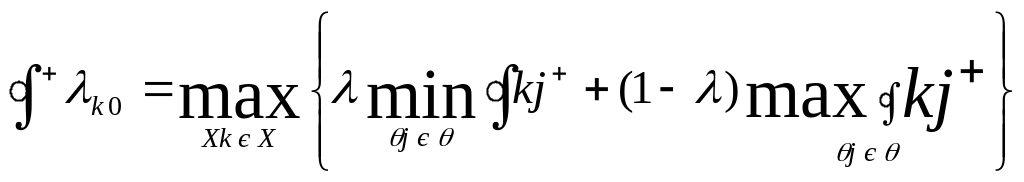
при фіксованому λ [0,1] .

Якщо позначити

, то з кожним рішенням xk X можна зв'язати показник:

, - показник Гурвіца рішення xk X .

Тут λ - коефіцієнт выражающий міру «песимізму» дослідника.

Проаналізуємо критерій Гурвіца:

При λ 0, - одержуємо критерій «крайнього оптимізму»;

при λ 1, - критерій перетворюється в песимистичний критерій Вальда;

при 0  λ 1, - одержуємо щось середнє між крайнім песимізмом і крайнім оптимізмом.

Коефіцієнт λ вибирається із суб'єктивних міркувань: чим опаснее ситуація, тим більше необхідно «подстраховаться», тим ближче λ до «1».

Значення є рівноважною точкою проміжку [0,1].

Можливе заперечення проти критерію Гурвіца: у деяких випадках оптимальні рішення суперечать здоровому глузду.

Приклад:

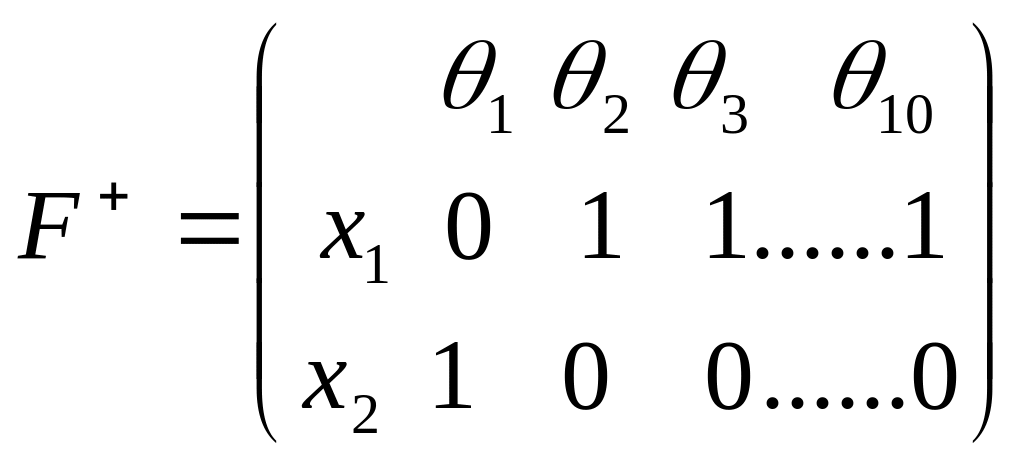
Відповідно до критерію Гурвіца обидва рішення оптимальні, - мають однаковий flk Проте x1 , явно краще чим x2 .

Тому, у критерії Гурвіца необхідно враховувати обмеження, наприклад, виду:

для будь-якого xk X , досліджуваного на оптимальність.

У загальному випадку оптимальне рішення за критерієм Гурвіца є функцією від λ і утворить ломану називану кривою Гурвіца.

Критерій Гурвіца для F.

У даному випадку повинно виконуватися умова:

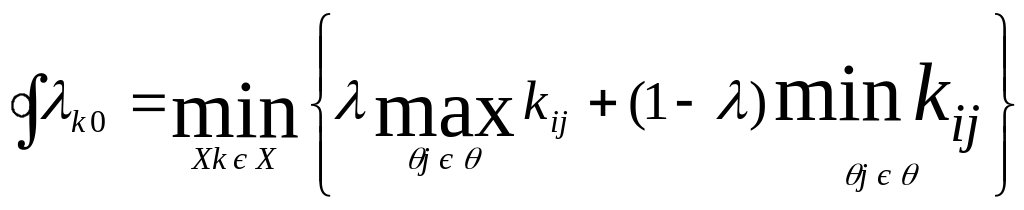
тобто при λ 1 - крайній песимізм (критерій Севіджа);

λ 0 - крайній оптимізм (мінімальний ризик із усіх можливих ситуацій).

Критерій Ходжеса-Лемана.

На практиці в процесі ухвалення рішення в умовах невизначеності інформація про стани середовища часто знаходиться між повним незнанням і точною вказівкою апріорного розподілу. Критерій Ходжеса - Лемана в деякому сенсі являє собою «суміш» критеріїв Байєса і Вальда. У даному випадку обмежене Байєсово рішення xko може бути визначене з умови:

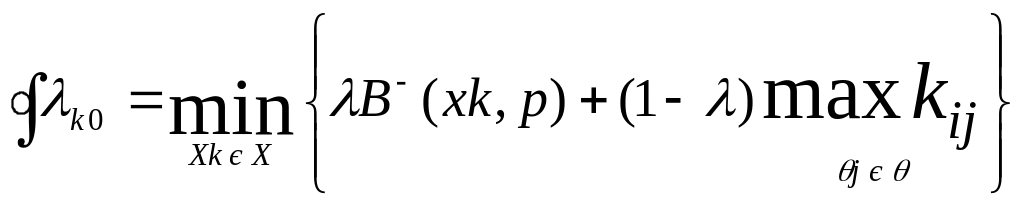
29. Організація ефективного управління в умовах конфлікту і невизначеності. Загальні положення.

Статична модель прийняття рішень породжена теоретико - ігровою концепцією. Під теорією ігор розуміють теорію математичних моделей і методів прийняття раціональних рішень в умовах конфлікту і невизначеності.

Під ситуацією прийняття рішень розуміють трійку {X,Θ, F}, де

X {x1,x2,...,xm } , - множина рішень;

{q1,q2 ,...,qn}, - множина станів економічного середовища, що може знаходиться в однім із цих станів;

F { fkj}, - функціонал оцінювання (матриця оцінного функціонала).

У розгорнутій формі ситуація прийняття рішень характеризується матрицею, елементи fkj якої є кількісними оцінками прийнятого рішення:

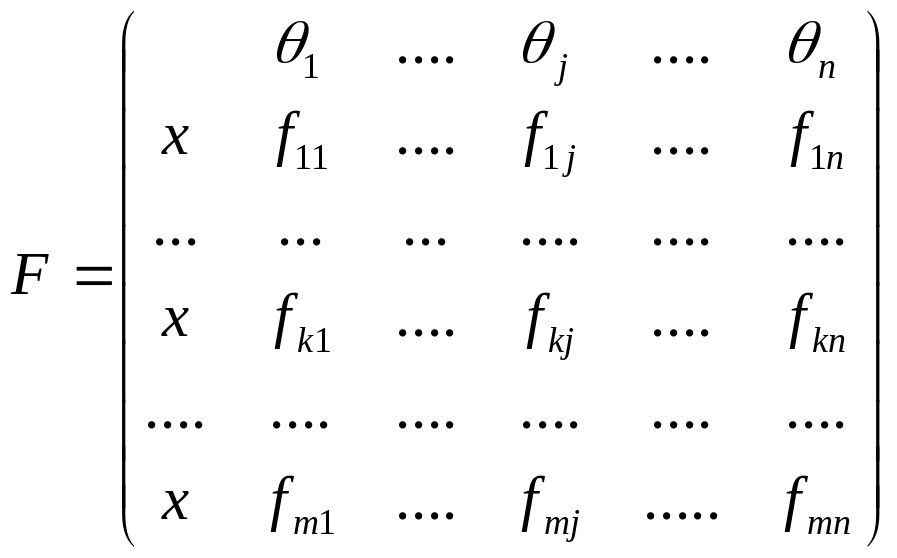
30. Принцип мінімаксу. Нижня і верхня ціна гри.

Розглянемо парну кінцеву гру що має розмірність mn . Нехай гравець A має m особистих стратегій, які позначимо A1, A2,...,Am , а гравець B має n особистих стратегій B1,B2,...,Bn . Позначив aij (aij ) виграш гравця A (програш гравця B ) складемо платіжну матрицю або матрицю гри, що представимо у вигляді табл. 1. Рядки цієї таблиці відповідають стратегіям гравця A , а стовпчики - стратегіям гравця. B .

Ai\Bj	B1	B2	....	Bn	aj
A1	a 11	a 12	.....	a 1n	a1
A2	a 21	a22	.....	a2n	a2
.....	....	.....	....	....	....
Am	am1	am2	....	amn	am
β j	β 1	β 2	....	β n

Поставимо задачу: визначити найкращу серед стратегій A1, A2,...,Am . Проаналізуємо послідовно кожну з них. Обираючи стратегію Ai , гравець A повинен розраховувати, що гравець B відповість на неї тієї із стратегій Bj , для якої виграш гравця A мінімальний (гравець B прагне «нашкодити» гравцю A ). Позначимо через ai , найменший виграш гравця A при виборі ним стратегії Ai , для всіх можливих стратегій гравця B :

Серед усіх чисел a_i (i =1,2,...,m) виберемо найбільше:

Значення a називають нижньою ціною гри, або максимальним виграшем (максиміном), тобто це гарантований виграш гравця A при будь-якій стратегії гравця B :

Стратегія, що відповідає максиміну, називається максимінною стратегією.

Гравець B зацікавлений у тому, щоб зменшити виграш гравця A , обираючи стратегію Bj , він візьме до уваги максимально можливий при цьому виграш для A . Випишемо внизу матриці максимальні значення a_ij по стовпчиках:

Серед усіх чисел b j виберемо найменше:

і назвемо b верхньою ціною гри або мінімаксним виграшем (мінімаксом). Це гарантований програш гравця B . Отже,

Стратегія, що відповідає мінімаксу, називається мінімаксною стратегією. Мінімаксні стратегії є стійкими у тому випадку, якщо одна зі сторін притримується своєї мінімаксної (максимінної) стратегії, то інша сторона не може поліпшити своє положення, відступивши від своєї. Якщо верхня і нижня ціни гри збігаються, то загальне значення верхньої і нижньої ціни гри називається чистою ціною гри, або ціною гри:

a = b =v .

Такі ігри займають особливе місце в теорії ігор і називаються іграми із сідловою точкою. У матриці такої гри існує елемент, що є одночасно мінімальним у своєму рядку і максимальним у своєму стовпчику. У сідловій точці стратегії сторін оптимальні.

31. Рішення ігор у змішаних стратегіях.

Якщо гра не має сідловій точки, то застосування чистих стратегій не дасть оптимального рішення гри. У такому випадку можна одержати оптимальне рішення, випадковим перебором чистих стратегій.

Змішаною стратегією SA гравця А називається застосування чистих стратегій „A1, A2 ,...., Ai ,...., Am” із ймовірностями „p1, p2 ,...., pi ,...., pm” причому сума ймовірностей рівна

Змішані стратегії гравця А` записуються у виді матриці

Або у виді рядка S А =(p1, p2 ,..., p j ,..., pm ). Аналогічно змішані стратегії гравця A` позначаються:

або SB =(q1,q2 ,...,q j ,...,qn) , де сума ймовірностей появи стратегій дорівнює

Очевидно, що чисту стратегію можна вважати окремим випадком змішаної: усі стратегії, крім даної, мають ймовірності, рівні нулю, а дана - одиниці.

На основі принципу минимакса визначається оптимальне рішення (або рішення) гри: це пара оптимальних стратегій S^*A, S^*B у загальному випадку змішаних, що мають властивість: якщо один із гравців притримується своєї оптимальної стратегії, то другому не може бути вигідно відступати від своєї. Виграш, що відповідає оптимальному рішенню, називається ціною v гри . Ціна гри задовольняє нерівності:

a ≤n ≤b ,

де a і b - нижня і верхня ціни гри.

Основна теорема теорії ігор - теорема Неймана. Кожна кінцева гра має принаймні одне оптимальне рішення, можливо, серед змішаних стратегій.

Нехай S^*_A = (p₁^*,...., p_m^*) і S^*_B = (q₁^*,...., q_m^*) - пара оптимальних стратегій. Якщо чиста стратегія входить в оптимальну змішану стратегію з відмінною від нуля ймовірністю, то вона називається активною.

Справедлива теорема про активні стратегії: якщо один із гравців притримується своєї оптимальної змішаної стратегії, то виграш залишається незмінним і рівним ціні гри , якщо другий гравець невиходить за межі своїх активних стратегій.

Ця теорема має велике практичне значення - вона дає конкретні моделі перебування оптимальних стратегій при відсутності сідлової точки.

32. Спрощення ігор.

Якщо гра m  n не має седловій точки, то пошук її рішення, особливо при великих , m  n являє собою достатньо трудомістку задачу. Іноді цю задачу вдасться спростити, якщо заздалегідь «редуцировати» гру, тобто скоротити число стратегій шляхом викреслювання деяких зайвих.

Зайві стратегії бувають двох видів: які дублюють і заздалегідь невигідні.

Приступаючи до рішення будь-якої гри m  n, необхідно насамперед виконати такі процедури:

- подивитися, чи не має в матриці седловой точки: якщо є, рішення вже знайдене

- якщо седловой точки немає, порівняти між собою почленно стовпчики і рядки з метою

викреслювання що дублюють і заздалегідь невигідних стратегій;

- подивитися, чи не можна зменшити число стратегій шляхом заміни деяких груп чистих - змішаними.

33. Приведення матричної гри до задачі лінійного програмування.

Гра m  n в загальному випадку не має наочної геометричної інтерпретації. Її рішення достатньо трудомістке при великих m і n проте принципових трудностей не має, оскільки може бути зведена до рішення задачі лінійного програмування. Нехай гра m  n задана платіжною матрицею (aij) , ; . Гравець А має стратегії A1, A2,..., Ai ,...., Am ,а гравець В стратегіями В1, В2 ,...., Вi ,...., Вn . Необхідно визначити оптимальні стратегії S^*_A = (p₁^*, p₂^*,...., p_m^*) і S^*_B = (q₁^*, q₂^*,...., q_m^*), де p_i^*, q_j^* - можливості застосування відповідних чистих стратегій Ai ,Bj (деякі з них, що відповідають неактивним стратегіям, можуть бути рівними нулю); стратегії p₁^*+ p₂^*+...+p_m^* = 1, q₁^*+ q₂^*+....+ q_m^* =1

Оптимальна стратегія S_A^* повинна задовольняє наступній вимозі:

• забезпечувати гравцю А середній виграш, не менше, чим ціна гри n, при будь-якій стратегії гравця В і виграш, рівний ціні гри n при оптимальній стратегії гравця A .

Ціна гри поки невідома. Не порушуючи спільності можна припустити її рівною деякому позитивному числу n > 0 . Цього можна домогтися, зробивши всі елементи aij невід’ємними шляхом додавання до всіх елементів матриці (aij) достатньо велику величину I .

Якщо гравець А застосовує змішану стратегію S^*_A = (p₁^*, p₂^*,...., p_m^*) проти будь-якої чистої стратегії Bj гравця A , то він одержує середній виграш, або математичне чекання виграшу:

aj = a1 j p1 + a2 j p2 +...+ amj pm, (1 )

де , тобто елементи J-го стовпчика платіжної матриці почленно перемножуються на відповідні ймовірності стратегій , A1, A2,..., Ai ,...., Am і результати складаються. Для оптимальної стратегії S_A^* всі середні виграші не менше ціни гри n , тому одержуємо систему нерівностей:

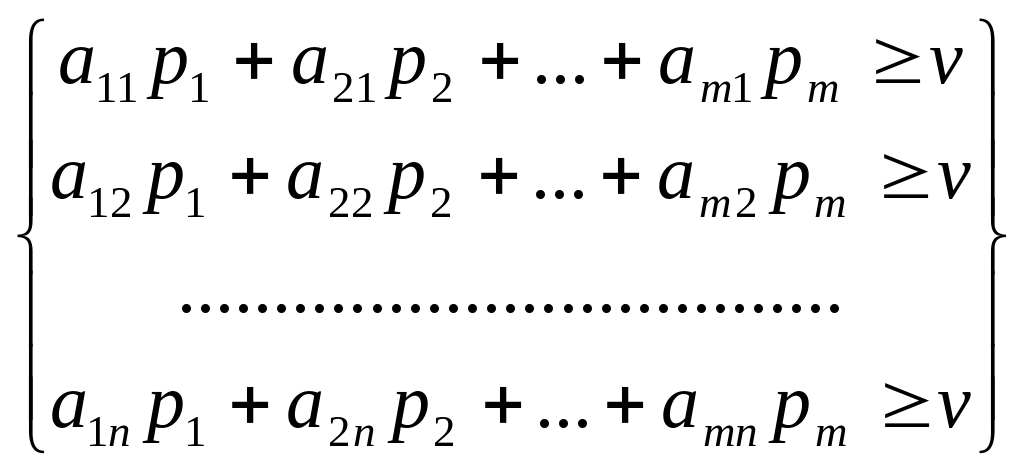(2)

Кожну з нерівностей можна поділити на число n > 0 і ввести нові змінні:

(3)

Тоді система (9.11) прийме вид:

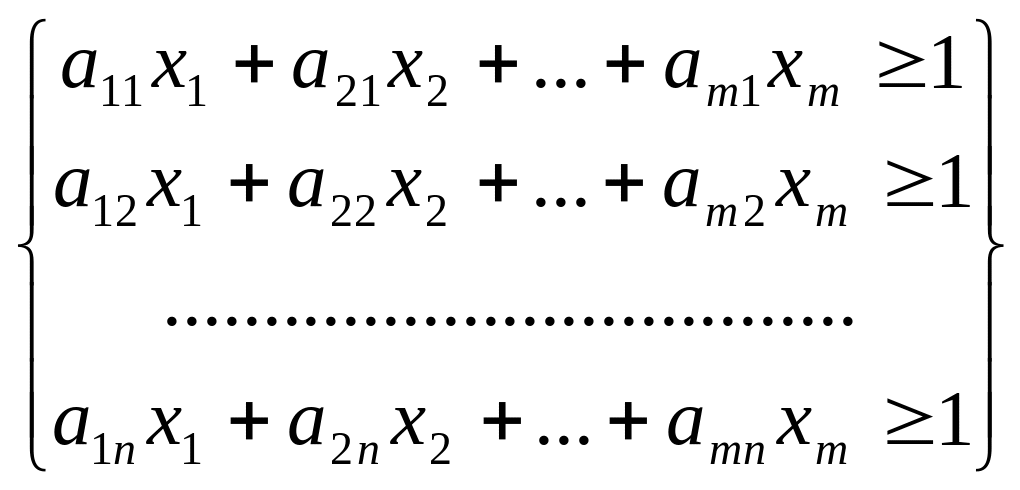(4)

Ціль гравця A - максимізувати свій гарантований виграш (ціну гри v ).

Розділивши на v0 рівність p1 + p2 +...+ pm =1, одержуємо, що змінні xi (i =1,2,...,m) задовольняють умові:

(5)

Максимизация ціни гри v еквівалентна мінімізації величині ( - ціна гри) тому задача може бути сформульована в такий спосіб: визначити значення xi ≥0, i =1,2,...,m перемінних , так, щоб вони задовольняли лінійним обмеженням (1) і при цьому лінійна функція

L = x1 + x2 + ...+ xm (6)

оберталася в мінімум.

Це задача лінійного програмування. Вирішуючи задачу (4) - (6), одержуємо оптимальне рішення p₁^*, p₂^*,...., p_m^* й оптимальну S^*_A

Для визначення оптимальної стратегії S^*_B = (q₁^*, q₂^*,...., q_m^*) варто врахувати, що гравець A прагне минимизировать гарантований виграш, тобто знайти Змінні q1,q2,...,qn удовлетворяют

неравенствам 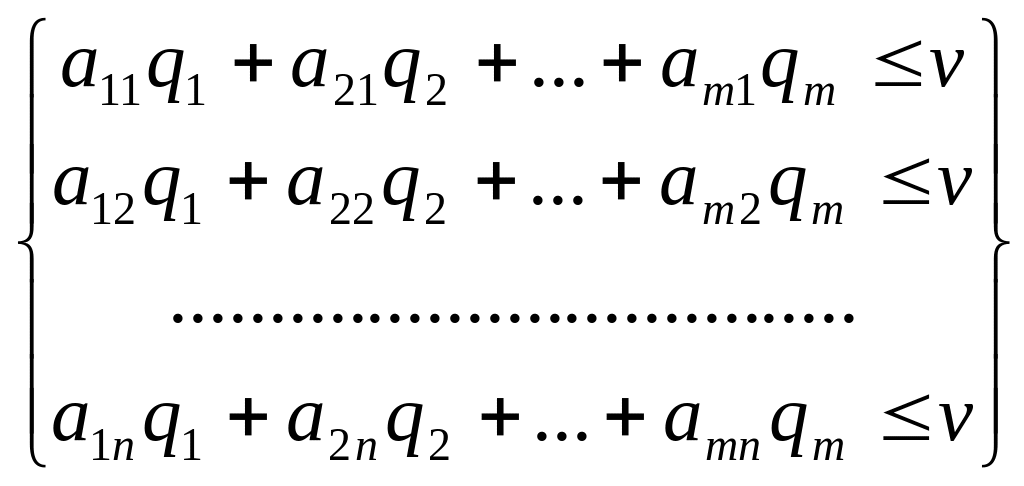(7)

які випливають із того, що середній програш гравця В не перевершує ціни гри, яку б чисту стратегію не застосовував гравець А.

Якщо позначити (8)

то одержимо систему нерівностей:

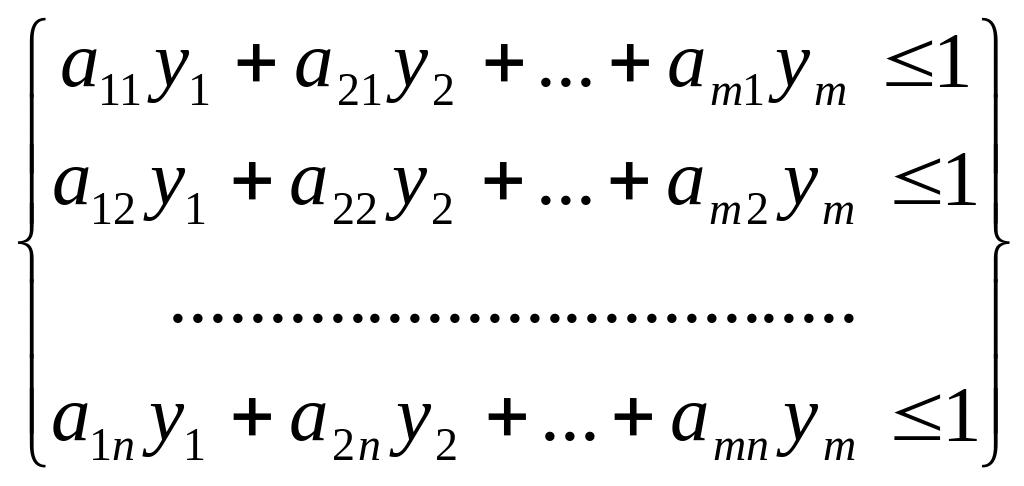(9)

Змінні y _j ( j =1,n) задовольняют умові

(10)

Гра звелася до наступної задачі. Визначити значення змінних yi ≥0, i =1,2,...,n, що задовольняють системі нерівностей (9) і максимізують лінійну функцію

Z = y1 + y2 + ...+ yn. (11)

Рішення задачі лінійного програмування (9) - (11) визначає оптимальну стратегію S^*_B = (q₁^*, q₂^*,...., q_m^*) При цьому ціна гри

(12)

Таким чином, оптимальні стратегії S^*_A = (p₁^*, p₂^*,...., p_m^*) і S^*_B = (q₁^*, q₂^*,...., q_n^*), ігри з матрицею (aij) розмірністю m  n можуть бути знайдені шляхом рішення симетричної пари двоїстих задач лінійного програмування.

Вихідна задача	Двоїста задача

34. Невизначеність цілей та компроміси Парето.

35. Економічна сутність і постановка окремих задач нелінійного програмування (Н.Л.П.).

У залежності від характеру розв’язуваних задач, особливостей методів, які застосовуються для розв’язку задач, всі моделі дослідження операцій поділяють на класи. Слід відзначити великий клас моделей оптимізації. Такі задачі виникають при спробі оптимізувати планування і управління складними системами, в першу чергу економічними. Оптимізацій ну задачу можна сформулювати в загальному вигляді: знайти змінні x₁ , x₂ , ..., xn , які задовольняють систему нерівностей рівнянь

і перетворюють в максимум (мінімум) цільову функцію, тобто

Якщо критерій ефективності і (або) система обмежень задаються нелінійними функціями, то це є задача нелінійного програмування.

36. Оптимізація функції однієї змінної та багатьох змінних.

37. Метод множників Лагранжа.

Метод невизначених множників або метод невизначених множників Лагранжа - метод знаходження умовного оптимуму, запропонований італійським математиком Жозефом-Луї Лагранжем. Метод дозволяє звести задачу на відшукання умовного оптимуму до задачі на знаходження безумовного оптимуму.

Задача

Нехай потрібно знайти оптимум функції n змінних при s умовах

, де .

Невизначені множники

Вводячи s невизначених множників Лагранжа λi, побудуємо функцію

.

Задача знаходження умовного оптимуму зводиться до розв'язування системи n+s рівнянь із n+s змінними:

.

Використання

Метод невизначених множників Лагранжа широко використовується в математичній і теоретичній фізиці. За допомогою цього методу отримані рівняння Лагранжа першого роду, які дозволяють формально ввести сили реакції в фізичні задачі із в'язями. Невизначені множники Лагранжа використовує також варіаційний метод в квантовій механіці.

38. Економічна сутність, деякі основні задачі та моделі динамічного програмування.

Задачі ДП є багатоетапними чи багатокроковими. Іншими словами, знаходження розв`язку конкретних задач методами ДП включають декілька етапів чи кроків, на кожному з яких визначається розв`язок деякої окремої задачі, обумовленою початковою. Тому термін “динамічне програмування” не стільки визначає собою тип задач, скільки характеризує методи знаходження розв`язку окремих класів задач математичного програмування, які можуть відноситися до задач як лінійного, так і нелінійного програмування. Не дивлячись на це, доцільно дати загальну постановку задачі ДП і визначити єдиний підхід до її розв`язку.

Економічну інтерпретацію загальної задачі ДП розглянемо на конкретних прикладах.

У розпорядження міністерства, у підпорядкуванні якого знаходиться k підприємств, виділено кошти в розмірі К тис. грн. для використання їх на розвиток підприємств протягом m років. Ці кошти на початку кожного господарського року, тобто в моменти t1, t2, …, tm , розприділяються між підприємствами. Одночасно з цим між підприємствами розподіляється отриманий ними за минулий рік прибуток. Таким чином, на початок кожного і-го року періоду, який нас цікавить j-те підприємство отримує в своє розпорядження хi( j ) тис.грн. Задача полягає у визначенні таких значень xi( j ) , тобто в знаходженні таких розподілів виділених коштів між підприємствами і прибутку що ними отримується, при яких за m років забезпечується отримання максимального прибутку всіма підприємствами.

Сформулювати поставлену задачу в термінах загальної задачі ДП.

Розв`язок. Припускаючи, що j-му підприємству на і-ий рік виділяється xi(j) тис. грн., будемо розглядати даний розподіл коштів як реалізацію деякого управління ui . Таким чином, управління ui полягає в тому, що на і-му кроці першому підприємству виділяється xi(1) тис. грн., другому - xi(2) тощо. Сукупність чисел xi(1), xi(2), …, xi(k) визначає всю сукупність управлінь u1, u2, …, um на m кроках розподілу коштів як m точок в k-вимірному просторі.

В якостікритерію оцінки якості обраного розподілу коштів, тобто реалізуючих управлінь, взятий сумарний прибуток за m років, який залежить від всієї сукупності управлінь:

W= W (u1, u2, …, um).

Отже, задача полягає у виборі таких управлінь ui*, тобто в такому розподілі коштів, при якому функція W приймає максимальне значення.

Сформульована задача є багатоетапною. Ця багатоетапність визначається її умовами, якими передбачено прийняття певних рішень на початку кожного року періоду часу, який розглядається. Разом з тим в цілому ряді інших задач ДП така багатоетапність безпосередньо не слідує з їх умов. Але в цілях знаходження розв`язку такі задачі доцільно розглядати як багатоетапні.

39. Багатокроковий процес прийняття рішень в динамічному програмуванні.

Будь-яку багатокрокову задачу можна розв’язувати по-різ­ному: або знаходити одразу всі елементи розв’язку на всіх кроках, або будувати оптимальне управління поступово, крок за кроком (на кожному етапі розрахунків оптимізуючи лише один крок). Як правило, другий спосіб оптимізації є значно прості­шим, ніж перший, особливо при значній кількості кроків. Опти­мізація одного кроку є простішою порівняно з оптимізацією всього процесу, тому краще багато разів розв’язувати простіші задачі, ніж один раз — складну.

Динамічний процес поділяється на сукупність послідовних етапів або кроків. На кожному етапі оптимізується тільки один крок, а рішення, під впливом якого система переходить з поточного стану в новий, вибирається з врахуванням його наслідків у майбутньому і не завжди дає найбільший ефект на даному етапі.

Плануючи багатокроковий процес, необхідно обирати управління на кожному кроці з урахуванням його майбутніх наслідків на тих кроках, які ще попереду. Лише на останньому кроці можна прийняти рішення, яке дасть максимальний ефект, оскільки наступного кроку для нього не існує. Тому оптимізація методом динамічного програмування починається з кінця, тобто спочатку планується останній крок. На базі відомої інформації про те, як закінчився попередній крок, для різних гіпотез щодо завершення передостаннього кроку вибирається управління на останньому. Таке управління називають умовно-оптимальним.

Для всіх кроків його знаходять із припущення, що попередній крок закінчився згідно з однією із можливих гіпотез.

Коли всі умовно-оптимальні управління на всіх кроках відомі, то це означає, що визначено, як необхідно керувати на кожному кроці, яким би не був процес на початку. В такому разі можна знайти не умовно-оптимальне, а оптимальне управління.

Дійсно, якщо відомо початковий стан , то можна вибрати для нього оптимальне управління , що приведе до стану , для якого також відоме оптимальне управління і т. д.

Отже, в процесі оптимізації управління методом динамічного програмування багатокроковий процес виконується двічі. Перший раз — від кінця до початку, в результаті чого знаходять умов­но-оптимальні управління і умовно-оптимальні виграші для всіх кроків. Другий раз — від початку до кінця, в результаті чого знаходять вже оптимальні покрокові управління, тобто оптимальне управління процесом у цілому.

Перший етап — знаходження умовно-оптимальних управлінь є дуже складним та довгим у порівнянні з другим. На другому етапі залишається лише «прочитати» рекомендації, що отримані на першому. Зауважимо, що «кінець» та «початок» можна поміняти місцями і здійснювати процес оптимізації також і в іншому напрямку (приклад 9.1).

Враховуючи вищезазначене, опишемо алгоритм розв’язування задач динамічного програмування, який складається з послідовності таких операцій:

1. Визначають специфічні показники стану досліджуваної керованої системи і множину параметрів, що описують цей стан. Стан системи описується у такий спосіб, щоб можна було забезпечити зв’язок між послідовними етапами розв’язання задачі і мати змогу одержати допустиме рішення задачі в цілому як результат оптимізації на кожному кроці окремо, а крім того, приймати оптимальні рішення на наступних етапах без урахування впливу майбутніх рішень на ті, що були прийняті раніше.

2. Поділяють процес на етапи (кроки), які, як правило, відповідають певним періодам планування динамічних процесів, або окремим об’єктам (підприємствам, видам продукції, устаткуванню тощо) у разі підготовки рішень стосовно керування ними.

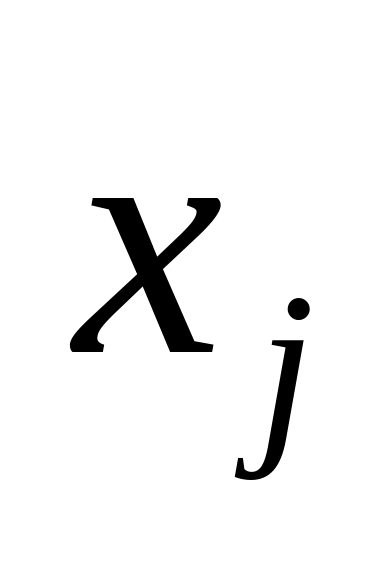
3. Формулюють перелік управлінь для кожного кроку і відповідні обмеження щодо них.

4. Визначають ефект, який забезпечує управління на j–му кроці, якщо перед тим система була у стані S, у вигляді функції ефективності:

.

5. Визначають, як змінюється стан S системи під впливом управління на j-му кроці, тобто як здійснюється перехід до нового стану:

.

6. Будують рекурентну залежність задачі динамічного програмування, що визначає умовний оптимальний ефект 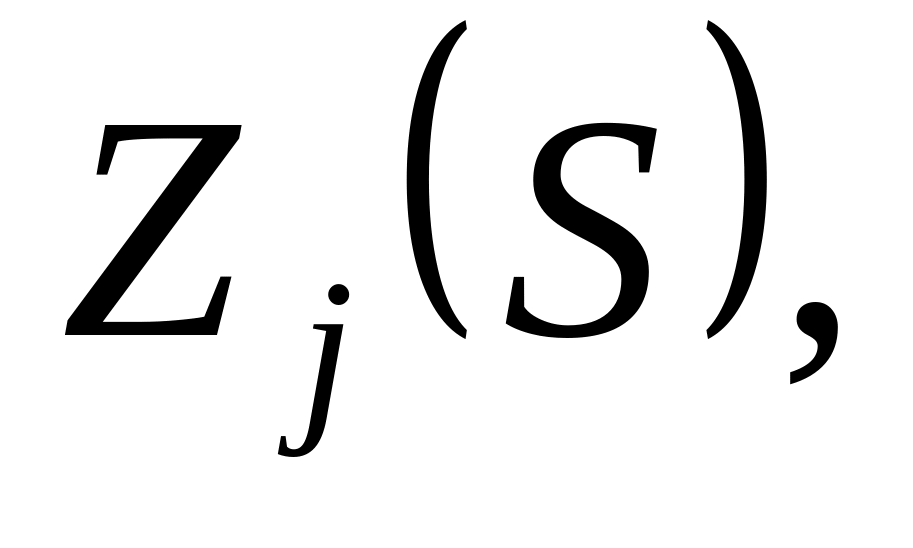починаючи з j–го кроку і до останнього, через вже відому функцію

.

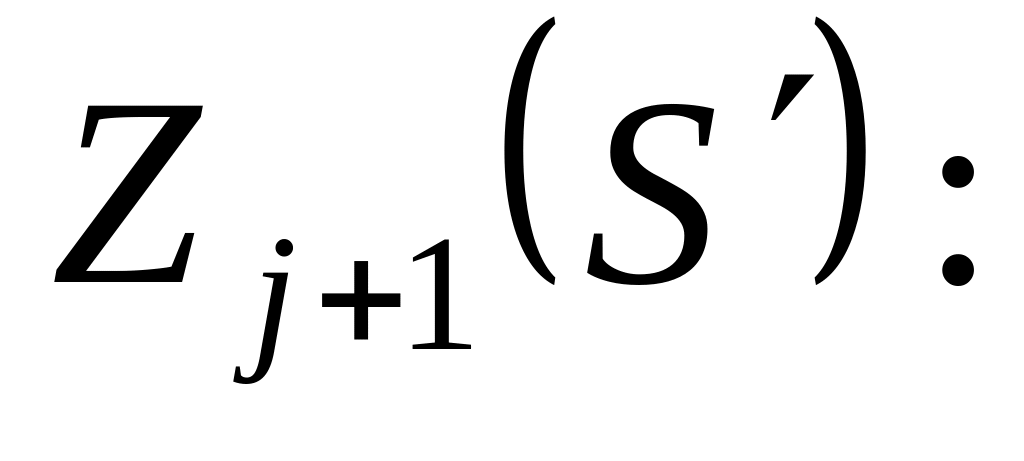
Цьому ефекту відповідає умовне оптимальне управління на j-му кроці Зауважимо, що у функції необхідно замість врахувати змінений стан системи, тобто

6. Використовують умовну оптимізацію останнього n-го кроку, визначаючи множину станів S, з яких можна за один крок дійти до кінцевого стану. Умовно-оптимальний ефект на n-му кроці обчислюють за формулою:

Потім знаходять умовно-оптимальне управління в результаті реалізації якого цей максимум буде досягнуто.

6. Проводять умовну оптимізацію 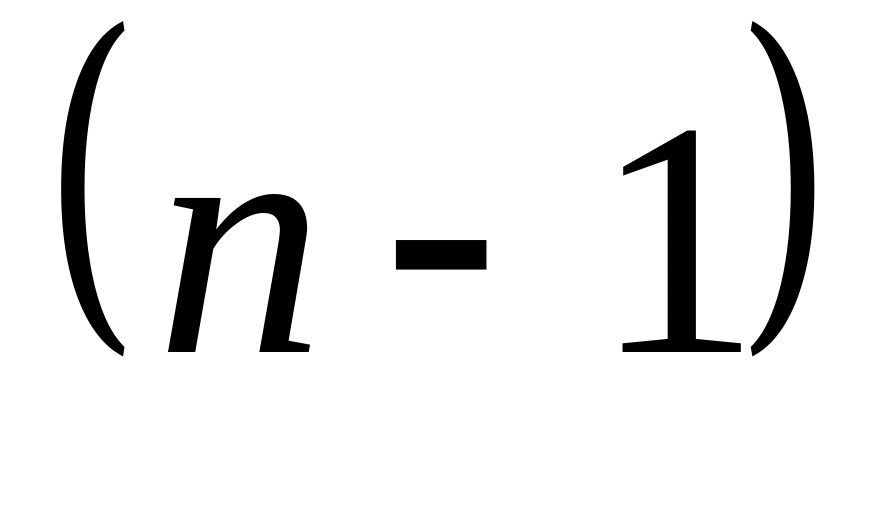-го, 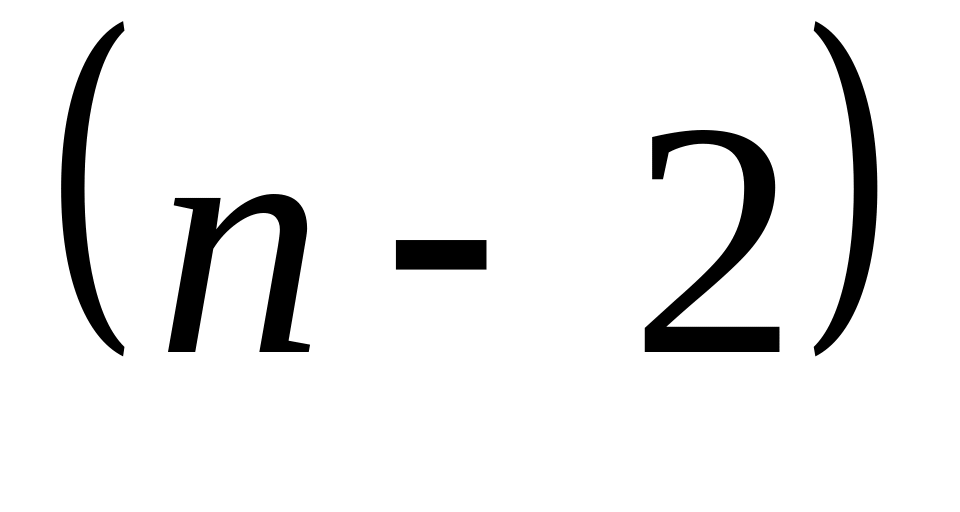-го та інших кроків за рекурентними залежностями (див. п. 6) і визначають для кожного кроку умовно-оптимальне управління:

6. Проводять безумовну оптимізацію управління у «зворотному» напрямку від початкового стану до кінцевого. Для цього з урахуванням визначеного оптимального управління на першому кроц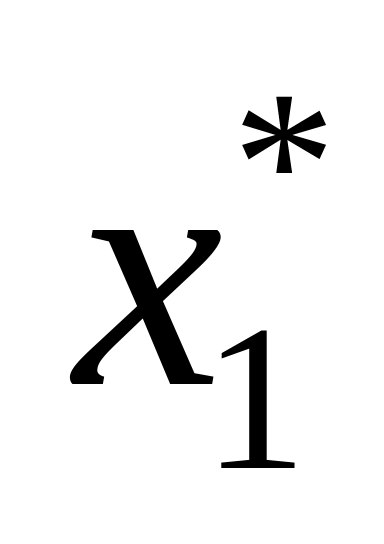і змінюють стан системи згідно з пунктом 5. Потім для цього нового стану знаходять оптимальне управління на другому кроці 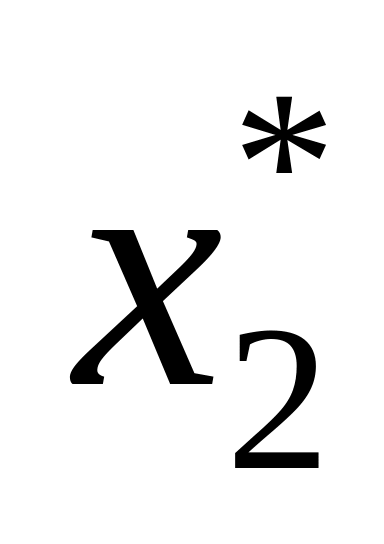і аналогічно ці дії повторюють до останнього етапу (кроку).

В результаті знаходять оптимальне покрокове управління , що забезпечує максимальну ефективність Z^*.

40. Принцип оптимальності Беллмана.

Будем считать, что состояние системы S на k-ом шаге (k=1, n) определяется совокупностью чисел X(k)=(x1(k), x2(k), …, xn(k)), которые получены в результате управления uk, обеспечивающего переход системы S из состояния X(k-1) в состояние X(k). При этом будем предполагать, что состояние X(k), в которое перешла система S, зависит от данного состояния X(k-1) и выбранного управления uk и не зависит от того, каким образом система пришла в состояние X(k-1).

Будем считать, что если в результате k-го шага обеспечен определенный доход или выигрыш, также зависящий от исходного состояния системы X(k-1) и выбранного управления uk и равный Wk(X(k-1), uk), то общий доход или выигрыш за n шагов составляет

Таким образом, сформулированы два условия, которым должна удовлетворять рассматриваемая задача динамического программирования. Первое условие называю условием отсутствия последействия, а второе – условием аддитивности целевой функции задачи.

Определение. Под оптимальной стратегией будем понимать совокупность управлений U*=(u1*, u2*, …, un*), в результате реализации которых система S за n шагов переходит из начального состояния X(0) в конечное состояние X(n) и при этом функция принимает наибольшее значение.

Принцип оптимальности Беллмана. Каково бы нибыло состояние системы перед очередным шагом, надо выбрать управление на этом шаге так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был максимальный.

Для этого нужно сделать различные предположения о том, как мог окончиться пред-последний шаг, и с учет этого выбрать управление un0, обеспечивающее максимальное зна-чение функции Wn(X(n-1), un). Такое управление, выбранное при определенных предположениях о том, как окончился предыдущий шаг, называется условно оптимальным управлением. Следовательно, принцип оптимальности требует находить на каждом шаге условно оптимальное управление для любого из возможных исходов предыдущего шага.

Fn(X(0)) - максимальный доход, получаемый за n шагов при переходе системы S из начального состояния X(0) в конечное состояние X(n) при реализации оптимальной стратегии управления U*=(u1*, u2*, …, un*), а через Fn-k(X(k)) – максимальный доход, получаемый при переходе из любого состояния X(k) в конечное состояние X(n) при оптимальной стратегии управления на оставшихся n-k шагах. Тогда

41. Задача про заміну обладнання підприємства

42. Структура та види запасів, ресурсів.

Задачі управління запасами складають один з найбільш численних класів економічних задач дослідження операцій, розв’язання яких має важливе народногосподарське значення. Правильне і своєчасне визначення оптимальної стратегії управління запасами, а також нормативного рівня запасів дозволяє вивільнити значні оборотні кошти, заморожені в виді запасів, що в кінцевому рахунку підвищує ефективність використання ресурсів. Розглянемо основні характеристики моделей управління запасами.

Попит. Попит на продукт, який запасається може бути детермінованим (в найпростішому випадку – постійним в часі) або випадковим. Випадковість попиту описується або випадковим моментом попиту, або випадковим обсягом попиту в детерміновані або випадкові моменти часу.

Поповнення складу. Поповнення складу може здійснюватися або через певні інтервали часу, або по мірі використання запасів, тобто зниження їх до деякого рівня.

Обсяг замовлення. При періодичному поповненні і випадковому використанні запасів обсяг замовлення може залежати від того стану, який спостерігається в момент подачі замовлення. Замовлення звичайно подається на одну і ту величину при досягненні запасом заданого рівня – так званої, точки замовлення.

Час доставки. В ідеалізованих моделях управління запасами припускається, що замовленепоповнення доставляється на склад миттєво. В інших моделях розглядається затримка поставок на фіксований або випадковий інтервал часу.

Вартість поставки. Як правило, припускається, що вартість кожної поставки складається з двохкомпонентів – разових витрат, які не залежать від обсягу замовленої партії, і витрат, що залежать, (частіше усього – лінійно) від обсягу партії.

Витрати зберігання. В більшості моделей управління запасами вважають обсяг складу практично необмеженим, а в якості величини, яку контролюють служить обсяг запасів, що зберігається. При цьому вважають, що за зберігання кожної одиниці запасу в одиницю часу стягується певна плата.

Штраф за дефіцит. Будь-який склад створюється для того, щоб запобігти дефіцитові певного типу виробів в обслуговуваній системі. Відсутність запасу в певний момент приводить до збитків, пов'язаних з простоями обладнання, неритмічністю виробництва тощо. Ці збитки в подальшому будемо називати штрафом за дефіцит.

Номенклатура запасу. В найпростіших випадках припускається, що на складі зберігається запас однотипних виробів або однорідного продукту. В більш складних випадках розглядається багатономенклатурний запас.

Структура складської системи. Найбільш повно розроблені математичні моделі одиночного складу. Однак на практиці зустрічаються і більш складні структури: ієрархічні системи складів з різноманітними періодами поповнення і часом доставки замовлень, з можливістю обміну запасами між складами одного рівня ієрархії тощо. В якості критерію ефективності прийнятої стратегії управління запасами виступає функція витрат, що подає сумарні витрати на зберігання і поставку продукту (в тому числі втрати від псування продукту при зберіганні і його морального старіння, втрати прибутку від омертвіння капіталу тощо) і витрати на штрафи.

43. Управління запасами.

Управління запасами полягає у відшуканні такої стратегії поповнення і витрат запасів при якому функція витрат приймає мінімальне значення. Нижче розглядаються найпростіші моделі управління запасами. Нехай функції A(t),B(t),R(t) виражають, відповідно, поповнення запасів, витрати і попит на продукт, запас якого формується протягом часу [0;t]. В моделях управління запасами звичайно використовуються похідні цих функцій за часом a(t), b(t), r(t) , що називаються, відповідно, інтенсивностями поповнення запасів, витрат і попиту. Якщо функції a(t), b(t), r(t) – не випадкові величини, то модель управління запасами вважається детермінованою, якщо хоча б одна з них носить випадковий характер – стохастичною. Якщо всі параметри моделі не змінюються в часі, вона називається статичною, в противному випадку – динамічною. Статичні моделі використовуються, коли приймається разове рішення про рівень запасів на певний період, а динамічні – у випадку прийняття послідовних рішень про рівень запасу або коригування раніше прийнятих рішень з урахуванням виникаючих змін.

Рівень запасу в момент t визначається основним рівнянням запасів:

J(t) = J₀ + A(t) – B(t), (1)

де J0 – початковий запас в момент t=0 .Рівняння (1) частіше використовується в інтегральній формі:

О(е) = О₀ + аф(е)ве – аи(е)ве (2)

44. Задачі управління виробництвом та резервами (визначення оптимальної області маневрування з врахуванням непрямого резерву)

45. Задачі управління виробництвом та резервами (обчислення оптимальної області маневрування з врахуванням взаємозаміни матеріальних ресурсів)

46. Задачі управління виробництвом та резервами (обчислення оптимальної області маневрування з врахуванням прямого резерву матеріальних ресурсів)

47. Задачі управління виробництвом та резервами (обчислення та узгодження виробничої програми з оптимальною областю маневрування)

48. Запаси, резерви як способи зниження ризику.

Одним з основних способів мінімізації ризику є створення запасів і резервів.

Мета – уникнення ризику призупинення діяльності господарюючого суб'єкта внаслідок нестачі матеріальних і інших ресурсів. До запасів крім предметів та продуктів праці належать запаси виробничих потужностей, обігових коштів, незавершеного виробництва, кваліфікації кадрів тощо.

Матеріальні запаси можна поділити на три види:

• страховий запас готової продукції на складі;

• страховий виробничий запас;

• динамічний страховий запас.

Створення резерву грошових коштів здійснюється з метою покриття випадкових затрат, при цьому виділяють два види резервів:

загальний резерв грошових коштів покликаний покривати будь-які зміни в кошторисі спричинені впливом факторів ризику;

спеціальний резерв, що складається з надбавок не покриття зростання цін і різних затрат за окремими позиціями.

Створення запасів і резервів на підприємстві є досить дієвим способом захисту від ризику, але і відносно “дорогим”, оскільки вимагає вилучення грошових коштів з господарського обороту.

49. Статична детермінована модель без дефіциту

Припущення про те, що дефіцит не допускається, означає повне задоволення попиту на продукт що запасається, тобто збіг функцій r(t) = b(t). Нехай загальне споживання продукту, за інтервал часу q дорівнює N. Розглянемо найпростішу модель, в якій припускається, що витрачання запасу відбувається безперервно з постійною інтенсивністю, тобто b(t) = b. Цю інтенсивність можна знайти, поділивши загальне споживання продукту на час, за який він витрачається:

b = N/Θ

Поповнення замовлення відбувається партіями однакового обсягу, тобто Функція a(t) не є неперервною: a(t)=0 при всіх t окрім моментів поставки продукту, коли a(t)=n, де n – обсяг партії. Оскільки інтенсивність витрат рівна b, то вся партія буде використана за час:

T = n/b (2).

Якщо відлік часу почати з моменту надходження першої партії, то рівень запасу в початковий момент дорівнює обсягу цієї партії n, тобто J(0)=n. Графічно рівень запасу в залежності від часу показано на рис. 1.

За інтервал часу [0;T] рівень запасу зменшується по прямій J(t) = n –bt від значення n до нуля. Оскільки дефіцит не допускається, то в момент T рівень запасу миттєво поповнюється до колишнього значення n за рахунок надходження партії замовлення. І так процес повторюється на кожному інтервалі часу тривалістю T.

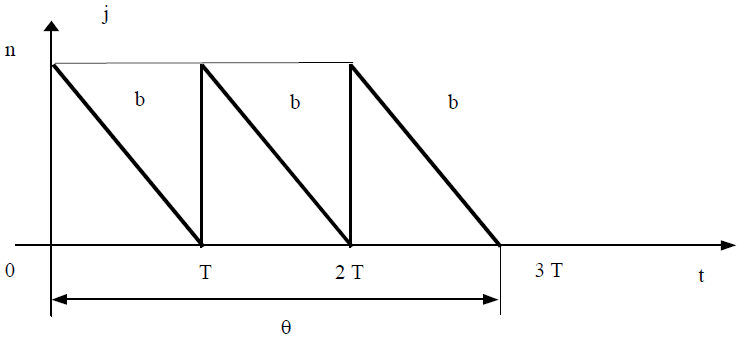
Рис. 1. Статична детермінована модель без дефіциту

Задача управління запасами полягає у визначенні такого обсягу партії n, за якого сумарні

витрати на створення і зберігання запасу були б мінімальними. Позначимо сумарні витрати через C, витрати на створення запасу – через C1, а витрати на зберігання запасу – через C2 і знайдемо ці величини за весь проміжок часу T.

Нехай витрати на доставку однієї партії продукту, не залежні від обсягу партії, рівні C1, а витрати на зберігання однієї одиниці продукту в одиницю часу – C2. Оскільки за час q необхідно сформувати запас у розмірі N одиниць продукту, що доставляється партіями в розмірі n одиниць, тоді число таких партій дорівнює k:

k = N/n = Θ/T. (3)

Звідси маємо:

C1 = c1*k = c1*(N/n). (4)

Середній запас за проміжок [0;T] дорівнює (n*T)/2,тобто витрати на зберігання усього запасу, за лінійних (в часі) його витратах, рівні витратам на зберігання середнього запасу. Враховуючи періодичність функції J(t) (усього за проміжок часу Θ буде k=N/n "зубців", аналогічних розглянутому на відрізку[0;T], і формулу (3), одержуємо, що витрати на зберігання запасу за проміжок часу Θ дорівнюють:

C2 = k*(c2*n*T)/2. (5)

Не важко помітити, що витрати C1 обернено пропорційні, а витрати C2 прямо пропорційні обсягу партії n. Графіки функцій C1(n) і C2(n), а також функції сумарних витрат наведені на рис. 2.

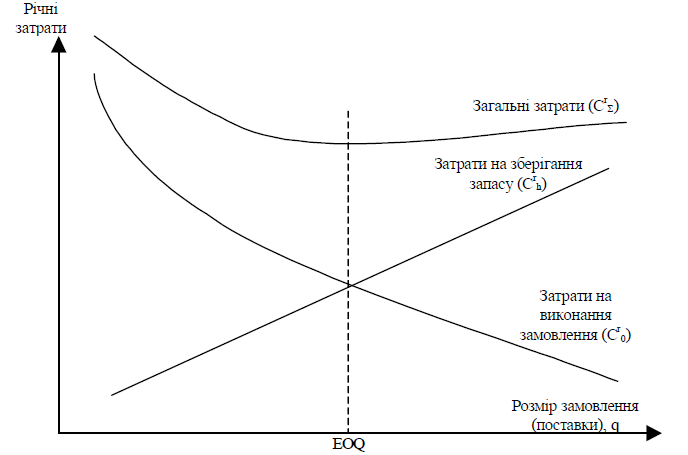
Рис. 2. Витрати на формування запасів

C = (c1*N)/n + n×(c2*Θ)/2. (6)

Розв’язавши задачу пошуку екстремуму цільової функції одержимо значення оптимального обсягу замовлення:

(7)

Виходячи з цього менеджеру треба розуміти, що мінімум загальних витрат задачі управління запасами досягається тоді, коли витрати на створення запасу рівні витратам на зберігання запасу.

При цьому мінімальні сумарні витрати:

C0 = C(n0) = (2*c1*N)/n0. (8)

Число оптимальних партій поставок за час q дорівнює:

k0 =×N/n0. (9)

Час витрат оптимальної партії, виходячи з формули (2) та з урахуванням (1) і (7) дорівнюватиме:

Т0 = n0/b. (10)

50. Статична детермінована модель з дефіцитом

В даній моделі будемо вважати наявність дефіциту. Це означає, що за відсутності продукту, запас якого формується, тобто при J(t)=0, попит зберігається з тією ж інтенсивністю r(t)=b, але споживання запасу буде відсутнє b(t)=0, внаслідок чого формується дефіцит зі швидкістю b, Графік зміни рівня запасу для цього випадку показаний на рис. 1. Спадання графіку нижче осі абсцис в область негативних значень характеризує формування дефіциту. З рис. 1 видно, що кожний період T=n/b розбивається на два тимчасових інтервали –– Т=Т1+Т2, де Т1 – час, протягом якого виробляється споживання запасу, Т2 – час, коли запас буде відсутній і нагромаджується дефіцит, що буде перекритий в момент надходження наступної партії. Необхідність покриття дефіциту призводить до того, що максимальний рівень запасу S в момент надходження кожної партії тепер не рівний її обсягу n, а менш нього на величину дефіциту n - s, що накопичився за час Т2 (рис. 1). З геометричних міркувань легко встановити, що T1 = (s/n)/T, T1 = T*(n – s)/n. Вданій моделі в функцію сумарних витрат C наряду з витратами c1 (на поповнення запасу) і c2 (на зберігання запасу) необхідно ввести витрати c3 – штраф через дефіцит:

С= c1+c2+c3.

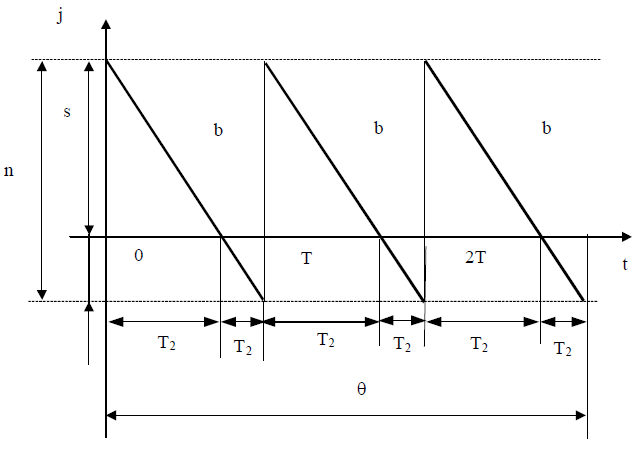
Рис. 1. Статична, детермінована модель з дефіцитом

Застосувавши математичні перетворення, одержуємо формули оптимального обсягу партії n0 і максимального рівня запасу s0 для моделі з дефіцитом (за допомогою достатньої умови екстремуму можна переконатися в тому, що дійсно при n=n0, s=s0функція C(n,s) досягає мінімуму):

де p – щільністю збитків із-за незадоволеного попиту:

p = c3/(c2 + c3).

p грає важливу роль в управлінні запасами. Відмітимо, що 0 ≤ p ≤ 1. Якщо значення с3 мале у порівнянні з с2, то величина p близька до нуля; коли с3 значно переважає с2, – r близька до 1. Неприпустимість дефіциту рівносильна припущенню, що с3=∞ або p=1. Отже, оптимальний обсяг партії в задачі з дефіцитом завжди більше (в раз), ніж в задачі без дефіциту.

36. Оптимізація функції однієї змінної та багатьох змінних.

37. Метод множників Лагранжа.

Метод невизначених множників або метод невизначених множників Лагранжа - метод знаходження умовного оптимуму, запропонований італійським математиком Жозефом-Луї Лагранжем. Метод дозволяє звести задачу на відшукання умовного оптимуму до задачі на знаходження безумовного оптимуму.

Задача

Нехай потрібно знайти оптимум функції n змінних при s умовах

, де .

Невизначені множники

Вводячи s невизначених множників Лагранжа λi, побудуємо функцію

Задача знаходження умовного оптимуму зводиться до розв'язування системи n+s рівнянь із n+s змінними:

Використання

Метод невизначених множників Лагранжа широко використовується в математичній і теоретичній фізиці. За допомогою цього методу отримані рівняння Лагранжа першого роду, які дозволяють формально ввести сили реакції в фізичні задачі із в'язями. Невизначені множники Лагранжа використовує також варіаційний метод в квантовій механіці.

38. Економічна сутність, деякі основні задачі та моделі динамічного програмування.

Задачі ДП є багатоетапними чи багатокроковими. Іншими словами, знаходження розв`язку конкретних задач методами ДП включають декілька етапів чи кроків, на кожному з яких визначається розв`язок деякої окремої задачі, обумовленою початковою. Тому термін “динамічне програмування” не стільки визначає собою тип задач, скільки характеризує методи знаходження розв`язку окремих класів задач математичного програмування, які можуть відноситися до задач як лінійного, так і нелінійного програмування. Не дивлячись на це, доцільно дати загальну постановку задачі ДП і визначити єдиний підхід до її розв`язку.

Економічну інтерпретацію загальної задачі ДП розглянемо на конкретних прикладах.

У розпорядження міністерства, у підпорядкуванні якого знаходиться k підприємств, виділено кошти в розмірі К тис. грн. для використання їх на розвиток підприємств протягом m років. Ці кошти на початку кожного господарського року, тобто в моменти t1, t2, …, tm , розприділяються між підприємствами. Одночасно з цим між підприємствами розподіляється отриманий ними за минулий рік прибуток. Таким чином, на початок кожного і-го року періоду, який нас цікавить j-те підприємство отримує в своє розпорядження хi( j ) тис.грн. Задача полягає у визначенні таких значень xi( j ) , тобто в знаходженні таких розподілів виділених коштів між підприємствами і прибутку що ними отримується, при яких за m років забезпечується отримання максимального прибутку всіма підприємствами.

Сформулювати поставлену задачу в термінах загальної задачі ДП.

Розв`язок. Припускаючи, що j-му підприємству на і-ий рік виділяється xi(j) тис. грн., будемо розглядати даний розподіл коштів як реалізацію деякого управління ui . Таким чином, управління ui полягає в тому, що на і-му кроці першому підприємству виділяється xi(1) тис. грн., другому - xi(2) тощо. Сукупність чисел xi(1), xi(2), …, xi(k) визначає всю сукупність управлінь u1, u2, …, um на m кроках розподілу коштів як m точок в k-вимірному просторі.

В якостікритерію оцінки якості обраного розподілу коштів, тобто реалізуючих управлінь, взятий сумарний прибуток за m років, який залежить від всієї сукупності управлінь:

W= W (u1, u2, …, um).

Отже, задача полягає у виборі таких управлінь ui*, тобто в такому розподілі коштів, при якому функція W приймає максимальне значення.

Сформульована задача є багатоетапною. Ця багатоетапність визначається її умовами, якими передбачено прийняття певних рішень на початку кожного року періоду часу, який розглядається. Разом з тим в цілому ряді інших задач ДП така багатоетапність безпосередньо не слідує з їх умов. Але в цілях знаходження розв`язку такі задачі доцільно розглядати як багатоетапні.

39. Багатокроковий процес прийняття рішень в динамічному програмуванні.

Будь-яку багатокрокову задачу можна розв’язувати по-різ­ному: або знаходити одразу всі елементи розв’язку на всіх кроках, або будувати оптимальне управління поступово, крок за кроком (на кожному етапі розрахунків оптимізуючи лише один крок). Як правило, другий спосіб оптимізації є значно прості­шим, ніж перший, особливо при значній кількості кроків. Опти­мізація одного кроку є простішою порівняно з оптимізацією всього процесу, тому краще багато разів розв’язувати простіші задачі, ніж один раз — складну.

Динамічний процес поділяється на сукупність послідовних етапів або кроків. На кожному етапі оптимізується тільки один крок, а рішення, під впливом якого система переходить з поточного стану в новий, вибирається з врахуванням його наслідків у майбутньому і не завжди дає найбільший ефект на даному етапі.

Плануючи багатокроковий процес, необхідно обирати управління на кожному кроці з урахуванням його майбутніх наслідків на тих кроках, які ще попереду. Лише на останньому кроці можна прийняти рішення, яке дасть максимальний ефект, оскільки наступного кроку для нього не існує. Тому оптимізація методом динамічного програмування починається з кінця, тобто спочатку планується останній крок. На базі відомої інформації про те, як закінчився попередній крок, для різних гіпотез щодо завершення передостаннього кроку вибирається управління на останньому. Таке управління називають умовно-оптимальним.

Для всіх кроків його знаходять із припущення, що попередній крок закінчився згідно з однією із можливих гіпотез.

Коли всі умовно-оптимальні управління на всіх кроках відомі, то це означає, що визначено, як необхідно керувати на кожному кроці, яким би не був процес на початку. В такому разі можна знайти не умовно-оптимальне, а оптимальне управління.

Дійсно, якщо відомо початковий стан , то можна вибрати для нього оптимальне управління , що приведе до стану , для якого також відоме оптимальне управління і т. д.

Отже, в процесі оптимізації управління методом динамічного програмування багатокроковий процес виконується двічі. Перший раз — від кінця до початку, в результаті чого знаходять умов­но-оптимальні управління і умовно-оптимальні виграші для всіх кроків. Другий раз — від початку до кінця, в результаті чого знаходять вже оптимальні покрокові управління, тобто оптимальне управління процесом у цілому.

Перший етап — знаходження умовно-оптимальних управлінь є дуже складним та довгим у порівнянні з другим. На другому етапі залишається лише «прочитати» рекомендації, що отримані на першому. Зауважимо, що «кінець» та «початок» можна поміняти місцями і здійснювати процес оптимізації також і в іншому напрямку (приклад 9.1).

Враховуючи вищезазначене, опишемо алгоритм розв’язування задач динамічного програмування, який складається з послідовності таких операцій:

6. Визначають специфічні показники стану досліджуваної керованої системи і множину параметрів, що описують цей стан. Стан системи описується у такий спосіб, щоб можна було забезпечити зв’язок між послідовними етапами розв’язання задачі і мати змогу одержати допустиме рішення задачі в цілому як результат оптимізації на кожному кроці окремо, а крім того, приймати оптимальні рішення на наступних етапах без урахування впливу майбутніх рішень на ті, що були прийняті раніше.

7. Поділяють процес на етапи (кроки), які, як правило, відповідають певним періодам планування динамічних процесів, або окремим об’єктам (підприємствам, видам продукції, устаткуванню тощо) у разі підготовки рішень стосовно керування ними.

8. Формулюють перелік управлінь для кожного кроку і відповідні обмеження щодо них.

9. Визначають ефект, який забезпечує управління на j–му кроці, якщо перед тим система була у стані S, у вигляді функції ефективності:

.

10. Визначають, як змінюється стан S системи під впливом управління на j-му кроці, тобто як здійснюється перехід до нового стану:

.

6. Будують рекурентну залежність задачі динамічного програмування, що визначає умовний оптимальний ефект починаючи з j–го кроку і до останнього, через вже відому функцію

.

Цьому ефекту відповідає умовне оптимальне управління на j-му кроці Зауважимо, що у функції необхідно замість врахувати змінений стан системи, тобто

6. Використовують умовну оптимізацію останнього n-го кроку, визначаючи множину станів S, з яких можна за один крок дійти до кінцевого стану. Умовно-оптимальний ефект на n-му кроці обчислюють за формулою:

Потім знаходять умовно-оптимальне управління в результаті реалізації якого цей максимум буде досягнуто.

6. Проводять умовну оптимізацію -го, -го та інших кроків за рекурентними залежностями (див. п. 6) і визначають для кожного кроку умовно-оптимальне управління:

6. Проводять безумовну оптимізацію управління у «зворотному» напрямку від початкового стану до кінцевого. Для цього з урахуванням визначеного оптимального управління на першому кроці змінюють стан системи згідно з пунктом 5. Потім для цього нового стану знаходять оптимальне управління на другому кроці і аналогічно ці дії повторюють до останнього етапу (кроку).

В результаті знаходять оптимальне покрокове управління , що забезпечує максимальну ефективність Z^*.

40. Принцип оптимальності Беллмана.

Будем считать, что состояние системы S на k-ом шаге (k=1, n) определяется совокупностью чисел X(k)=(x1(k), x2(k), …, xn(k)), которые получены в результате управления uk, обеспечивающего переход системы S из состояния X(k-1) в состояние X(k). При этом будем предполагать, что состояние X(k), в которое перешла система S, зависит от данного состояния X(k-1) и выбранного управления uk и не зависит от того, каким образом система пришла в состояние X(k-1).

Будем считать, что если в результате k-го шага обеспечен определенный доход или выигрыш, также зависящий от исходного состояния системы X(k-1) и выбранного управления uk и равный Wk(X(k-1), uk), то общий доход или выигрыш за n шагов составляет

Таким образом, сформулированы два условия, которым должна удовлетворять рассматриваемая задача динамического программирования. Первое условие называю условием отсутствия последействия, а второе – условием аддитивности целевой функции задачи.

Определение. Под оптимальной стратегией будем понимать совокупность управлений U*=(u1*, u2*, …, un*), в результате реализации которых система S за n шагов переходит из начального состояния X(0) в конечное состояние X(n) и при этом функция принимает наибольшее значение.

Принцип оптимальности Беллмана. Каково бы нибыло состояние системы перед очередным шагом, надо выбрать управление на этом шаге так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был максимальный.

Для этого нужно сделать различные предположения о том, как мог окончиться пред-последний шаг, и с учет этого выбрать управление un0, обеспечивающее максимальное зна-чение функции Wn(X(n-1), un). Такое управление, выбранное при определенных предположениях о том, как окончился предыдущий шаг, называется условно оптимальным управлением. Следовательно, принцип оптимальности требует находить на каждом шаге условно оптимальное управление для любого из возможных исходов предыдущего шага.

Fn(X(0)) - максимальный доход, получаемый за n шагов при переходе системы S из начального состояния X(0) в конечное состояние X(n) при реализации оптимальной стратегии управления U*=(u1*, u2*, …, un*), а через Fn-k(X(k)) – максимальный доход, получаемый при переходе из любого состояния X(k) в конечное состояние X(n) при оптимальной стратегии управления на оставшихся n-k шагах. Тогда

41. Задача про заміну обладнання підприємства

42. Структура та види запасів, ресурсів.

Задачі управління запасами складають один з найбільш численних класів економічних задач дослідження операцій, розв’язання яких має важливе народногосподарське значення. Правильне і своєчасне визначення оптимальної стратегії управління запасами, а також нормативного рівня запасів дозволяє вивільнити значні оборотні кошти, заморожені в виді запасів, що в кінцевому рахунку підвищує ефективність використання ресурсів. Розглянемо основні характеристики моделей управління запасами.

Попит. Попит на продукт, який запасається може бути детермінованим (в найпростішому випадку – постійним в часі) або випадковим. Випадковість попиту описується або випадковим моментом попиту, або випадковим обсягом попиту в детерміновані або випадкові моменти часу.

Поповнення складу. Поповнення складу може здійснюватися або через певні інтервали часу, або по мірі використання запасів, тобто зниження їх до деякого рівня.

Обсяг замовлення. При періодичному поповненні і випадковому використанні запасів обсяг замовлення може залежати від того стану, який спостерігається в момент подачі замовлення. Замовлення звичайно подається на одну і ту величину при досягненні запасом заданого рівня – так званої, точки замовлення.

Час доставки. В ідеалізованих моделях управління запасами припускається, що замовленепоповнення доставляється на склад миттєво. В інших моделях розглядається затримка поставок на фіксований або випадковий інтервал часу.

Вартість поставки. Як правило, припускається, що вартість кожної поставки складається з двохкомпонентів – разових витрат, які не залежать від обсягу замовленої партії, і витрат, що залежать, (частіше усього – лінійно) від обсягу партії.

Витрати зберігання. В більшості моделей управління запасами вважають обсяг складу практично необмеженим, а в якості величини, яку контролюють служить обсяг запасів, що зберігається. При цьому вважають, що за зберігання кожної одиниці запасу в одиницю часу стягується певна плата.

Штраф за дефіцит. Будь-який склад створюється для того, щоб запобігти дефіцитові певного типу виробів в обслуговуваній системі. Відсутність запасу в певний момент приводить до збитків, пов'язаних з простоями обладнання, неритмічністю виробництва тощо. Ці збитки в подальшому будемо називати штрафом за дефіцит.

Номенклатура запасу. В найпростіших випадках припускається, що на складі зберігається запас однотипних виробів або однорідного продукту. В більш складних випадках розглядається багатономенклатурний запас.

Структура складської системи. Найбільш повно розроблені математичні моделі одиночного складу. Однак на практиці зустрічаються і більш складні структури: ієрархічні системи складів з різноманітними періодами поповнення і часом доставки замовлень, з можливістю обміну запасами між складами одного рівня ієрархії тощо. В якості критерію ефективності прийнятої стратегії управління запасами виступає функція витрат, що подає сумарні витрати на зберігання і поставку продукту (в тому числі втрати від псування продукту при зберіганні і його морального старіння, втрати прибутку від омертвіння капіталу тощо) і витрати на штрафи.

43. Управління запасами.

Управління запасами полягає у відшуканні такої стратегії поповнення і витрат запасів при якому функція витрат приймає мінімальне значення. Нижче розглядаються найпростіші моделі управління запасами. Нехай функції A(t),B(t),R(t) виражають, відповідно, поповнення запасів, витрати і попит на продукт, запас якого формується протягом часу [0;t]. В моделях управління запасами звичайно використовуються похідні цих функцій за часом a(t), b(t), r(t) , що називаються, відповідно, інтенсивностями поповнення запасів, витрат і попиту. Якщо функції a(t), b(t), r(t) – не випадкові величини, то модель управління запасами вважається детермінованою, якщо хоча б одна з них носить випадковий характер – стохастичною. Якщо всі параметри моделі не змінюються в часі, вона називається статичною, в противному випадку – динамічною. Статичні моделі використовуються, коли приймається разове рішення про рівень запасів на певний період, а динамічні – у випадку прийняття послідовних рішень про рівень запасу або коригування раніше прийнятих рішень з урахуванням виникаючих змін.

Рівень запасу в момент t визначається основним рівнянням запасів:

J(t) = J₀ + A(t) – B(t), (1)

де J0 – початковий запас в момент t=0 .Рівняння (1) частіше використовується в інтегральній формі:

О(е) = О₀ + аф(е)ве – аи(е)ве (2)

44. Задачі управління виробництвом та резервами (визначення оптимальної області маневрування з врахуванням непрямого резерву)

45. Задачі управління виробництвом та резервами (обчислення оптимальної області маневрування з врахуванням взаємозаміни матеріальних ресурсів)

46.Розглянемо питання розрахунку оптимального рівня виробництва для систем з нестійким попитом на готову продукцію, що характерно в умовах ринкової економіки.

Імовірнісний характер керованої системи, викликаний нестійкістю попиту, а також вимоги до стабільності ряду показників і наявність певних можливостей маневрування зумовлюють необхідність дослідження адаптивних властивостей рівня виробництва. 3 метою покращення техніко-економічних показників використовують резерви продукції та ресурсів. Розрізняють два види матеріальних резервів.

Прямі резерви, що являють собою запас (надлишок) матеріальних ресурсів, які є особливо дефіцитними при коригуванні рівня виробництва.

Непрямі резерви, що являють собою такий обсяг матеріальних ресурсів, узгоджених з рівнем виробництва, тобто необхідних для його виконання, який при можливому коригуванні цього рівня забезпечив би максимальне задоволення попиту на матеріальні ресурси, а затрати, викликані надлишком ресурсів, були б мінімальними.

47.Стратегія управління запасами при невизначеному (стохастичному) попиті вимагає створення певного резерву заздалегідь визначеного обсягу К, a потім здійснюються чергові поставки запасів. Якщо в певний момент часу загальний запас знижується до розмірів резерву, терміново оформляють заявку на постачання нової партії.

Задача управління запасами в умовах невизначеності та зумовленого нею ризику вимагає визначення оптимального резерву.

Одним з простих способів, що дає змогу вирішити проблему резерву, є застосування принципу гарантованого результату, тобто обрання досить великого резерву, який гарантує мінімальний ризик, тобто компенсацію будь-яких випадкових відхилень, що вимагає великих затрат щодо їх зберігання тощо. Це також веде до так званого ризику невикористаних можливостей, великі резерви пов’язані з відволіканням значних коштів. Тому вводяться додаткові гіпотези, в основу розрахунку необхідного резерву закладається поняття допустимого ризику — ймовірності того, що потреба в запасах не перевищить наявного резерву.

Вводиться поняття коефіцієнта ризику pz, який виражає імовірність того, що потреби у запасах виявляються незадовільними через недостатність резерву, перевищать його обсяг. Значення коефіцієнта ризику pz вибирається не більшим від певної фіксованої величини a — порогу дозволеності. Значення порогу дозволеності найчастіше покладають рівним 0.05, 0.025, 0.01 (відповідно 5%, 2.5%, 1%) тощо.

48. За нестабільного економічного середовища, несвоєчасного виконання прийнятих рішень, помилок в обґрунтуванні оптимального рівня планів тощо виникає істотний (навіть катастрофічний) рівень ризику. У зв’язку з цим менеджерам доцільно вживати відповідних заходів, створюючи резервні фонди (фонди ризику) для страхування несприятливих наслідків, зниження ступеня ризику.

Управління запасами пов’язане з проблемою досягнення оптимальної рівноваги між двома конкуруючими чинниками: мінімізацією капіталовкладень у запаси та максимізацією рівня надійності обслуговування споживачів продукцією даного підприємства.

До запасів, крім предметів і продуктів праці, належать запаси виробничих потужностей, основних фондів і оборотних коштів, незавершене будівництво, кваліфіковані кадри тощо.

49.Модель управління запасами простого типу характеризується сталим у часі попитом, миттєвим збільшенням запасу і відсутністю дефіциту.

Отже, сумарні витрати в одиницю часу С ( у ) як функцію від у можна представити у вигляді: сумарні витрати в одиницю часу С ( у ) - Витрати на оформлення замовлення за одиницю часу + Витрати на зберігання запасів за одиницю часу.

Таким чином, С ( у ) =

Оптимальне значення у отримується в результаті мінімізації С ( у ) по у . Таким чином, у припущенні, що у неперервна змінна, одержуємо:

, звідки оптимальне значення розміру замовлення визначається виразом , Оскільки друга похідна в точці у* строго додатна, досягається мінімум. Отриманий вираз для розміру замовлення, зазвичай, називають формулою економічного розміру замовлення Уілсона.

Оптимальна стратегія моделі передбачає замовлення у* через кожні

t₀^* = у^*/ одиниць часу. Оптимальні витрати С( у^* ), отримані шляхом безпосередньої підстановки, складають .

50,Ця модель призначена для системи управління запасами, яка містить п>1 видів продукції, що зберігається на одному складі з обмеженого площею. Дана умова визначає взаємозв’язок між різними видами продукції і може бути включена в модель як обмеження.

18. Базові показники підприємницького ризику. Чим бiльше коливаються i вiдхиляються доходи, тим вищий ризик. Цю мiнливiсть часто вимiрюють за доп. стандартного вiдхиленя. Ф-ла,що вiдображає величину очiкуваного доходу R i ступенем ризику мае вигляд: R=R_j+kσ_{p ,} де R _j- ,безпечна ставка доходу, σ_p - стандартне вiдхилення заданої комбiнацiї цiнних пап. з ризиковими та безриз. активами. Щоб виконувати матем. розрахунки рiвня ризику, потрiбно знати теорiю йм-сте, матем.моделювання та розумiти як ризик портфеля цiнних пап. i доходи поеднуються в своїй взаемозалежностi. Iснуе модель оцiнювання капiт. активiв (МОКА). МОКА подiляе ризик на 2 складовi: диферсифiкований ризик i недиферсиф. Iдеться про тiсний зв’язок мiж доходами окремих власникiв цiнних пап. i заг. доходами ринку цiнних пап. Модель лiнii надiйностi ринку

(ЛНР)показуе, що необхiдна величина дохiдностi активiв склад. з безпечної ставки та премiї за ризик. Фор-ла: R=R_f+(R_m – R_f) β_p , де R_f –безпечна ставка, R_m –сер. дохiднiсть ринку, β_p- недиверсифiкований ринок.

35. Економічна сутність і постановка окремих задач нелінійного програмування (Н.Л.П.). У залежності від хар-ру розв’язуваних задач, особливостей методів, які застос. для розв’язку задач, всі моделі ДО поділяють на класи. Слід відзначити великий клас моделей оптимізації. Такі задачі виникають при спробі оптимізувати планування і упр-ння складними сис-ми, в першу чергу екон. Оптиміз. задачу можна сформулювати в заг. вигляді: знайти змінні x₁ , x₂ , ..., xn , які задовольняють сис-му нерівностей рівнянь

і перетворюють в максимум (мінімум) цільову ф-цію, тобто

Якщо критерій еф-сті і (або) сис-ма обмежень задаються нелін. ф-ціями, то це є задача нелінійного програмування.

44.ВИЗНАЧЕННЯ ОПТИМАЛЬНОЇ ОБЛАСТІ МАНЕВРУВАННЯ З ВРАХУВАННЯМ НЕПРЯМОГО РЕЗЕРВУ.Непрямий резерв закладено в ресурсах, що використовуються під час виконання замовлення. Він враховує випадкові умови реалізації виготовленої продукції.

Оптимальна область маневрування з врахуванням непрямого резерву визначається за допомогою такої задачі: мінімізувати функцію сподіваних затрат (функцію ризику);

(11.12)

за умови (11.13)

де т — кількість матеріальних ресурсів, що використовуються в системі; і — номер матеріального ресурсу; —вектор області ма-

неврування; ' —випадковий вектор використання матеріаль-

них ресурсів;

(11.14)

— питомі затрати, викликані надлишком і-го матеріального ресурсу; — питомі_затрати, викликані дефіцитом і-го матеріального ресурсу; — вектор обсягу матеріальних ресурсів, необхідних для виконання обов'язкової програми випуску виробів;

(11.15)

п—кількість виробів, що виготовляються; а,у—норма витрат /-теріаяьного ресурсу на одину'-й виріб; щ —обов'язкова програма випуску /го виробу (це може бути замовленням або обсягом випуску, обу-мовленого угодами).

Для розв'язку задачі (11.12), (11.13) застосуємо метод стохас-тичних квазіградіентів [20, 59].

п—кількість виробів, що виготовляються; а,у—норма витрат /-теріаяьного ресурсу на одину'-й виріб; щ —обов'язкова програма випуску /го виробу (це може бути замовленням або обсягом випуску, обу-мовленого угодами).

Для розв'язку задачі (11.12), (11.13) застосуємо метод стохас-тичних квазіградіентів [20, 59]. п—кількість виробів, що виготовляються; а,у—норма витрат /-теріаяьного ресурсу на одину'-й виріб; щ —обов'язкова програма випуску /го виробу (це може бути замовленням або обсягом випуску, обу-мовленого угодами).

Для розв'язку задачі (11.12), (11.13) застосуємо метод стохас-тичних квазіградіентів [20, 59].

45. ОБЧИСЛЕННЯ ОПТИМАЛЬНОЇ ОБЛАСТІ МАНЕВРУВАННЯ З ВРАХУВАННЯМ ВЗАЄМОЗАМІНИ МАТЕРІАЛЬНИХ РЕСУРСІВ Якщо є можливість взаємозаміни матеріальних ресурсів для всіх виробів, що виготовляються, то розрахунок оптимальної області маневрування з врахуванням взаємозаміни /-го ресурсу у-м визначається розв'язанням такої задачі: мінімізувати функ­цію затрат, тобто функцію

де крїО, а/і 0, р,-2 0; У/=(ур /= 1» т; у= 1, л) —обсяг взаємозаміни /-го матеріального ресурсу у-м ресурсом; Ху — коефіцієнт взаємозаміни /-го ресурсу еониту у-м ресурсом; соу — випадковий вектор використання /-го ресурсу; Сі — ціна /-го ресурсу; ц—обсяг у-го матеріального ресурсу, необхідного для виконання обов'язкової програми випуску; у,—обсяг максимально можливого використання у-го ресурсу; о,-, р,-—відповідно шггомі затрати із-за надлишку та дефіциту у-го матеріального ресурсу.

Для розв'язання задачі (11.16), (11.17) також застосовується метод стохастичних квазіградієнтів з проектуванням.

*