Край поверхности и его ориентация.

Опр.:

1. Полупространством называется .

2. Краем полупространства называется

3. - полупространство без края.

Опр.:

называется поверхностью размерности с краем, если:

гомеоморфна либо , либо .

Если заменить в определении на (куб), а на (куб с одной присоединённой гранью), то определение останется эквивалентным.

Опр.:

Точка называется точкой края, если она имеет окрестность гомеоморфную .

Опр.:

Совокупность точек края поверхности с краем называется краем поверхности.

Пример:

- замкнутый шар

- сфера

Согласование ориентации поверхности и её края

Опр.:

Если - ориентирующий атлас стандартных локальных карт поверхности с краем , то -ориентирующий атлас края. Задаваемая им ориентация края называется ориентацией края, согласованной с ориентацией поверхности.

Пример:

- согласованы

Непрерывным преобразованием подводим его к краю. Первый вектор направляем по нормали. Остальные векторы задают ориентацию поверхности.

Согласованность определяется по правилу буравчика.

Касательное пространство к поверхности

- матрица Якоби в точке

- касательное пространство к поверхности в точке .

Утв.: состоит из касательных прямых, проведённых к кривым, проходящим через точку и принадлежащим .

Касательная к поверхности в

- координатные линии

- касательный вектор к координатной линии

- вектор нормали в точке

- уравнение касательной плоскости в векторной форме

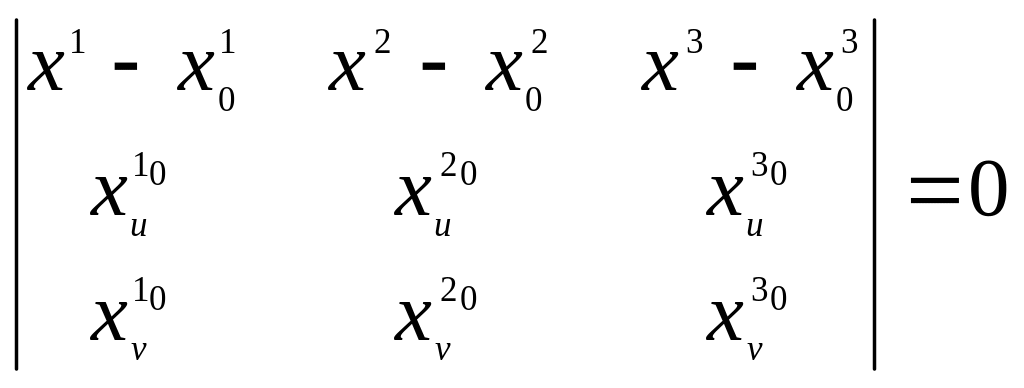- уравнение касательной плоскости в координатной форме

Пример 1:

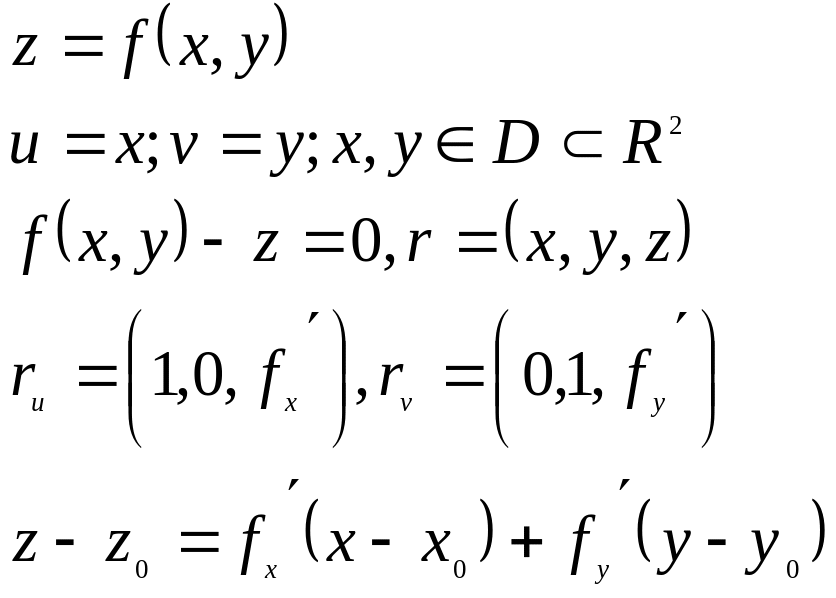
Пример 2:

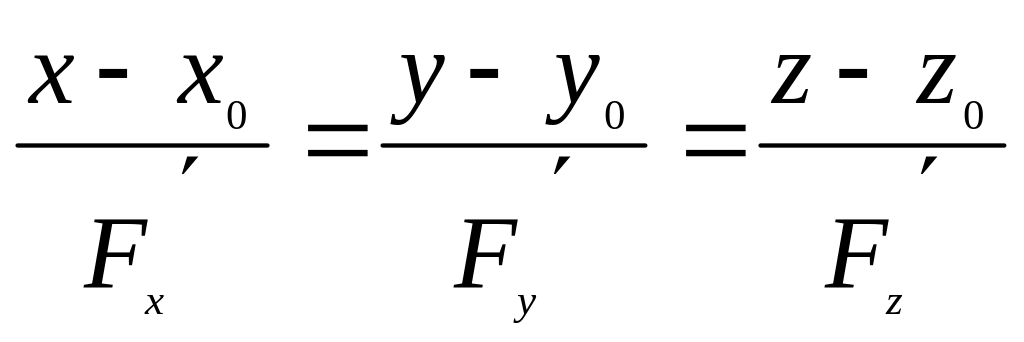- нормаль

Лекция 9

Площадь поверхности в Евклидовом пространстве

1.

- ортонормированный базис

- ориентированный объём парал-да, натянутого на векторы

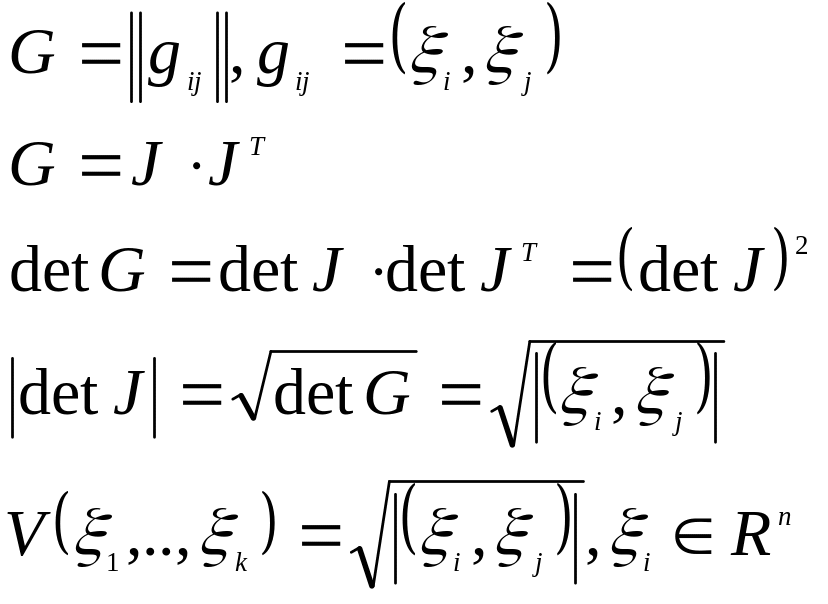
2. - -мерная поверхность в

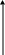
- некий криволинейный параллелепипед в

- параллелепипед на касательном пространстве

- объём параллелепипеда, натянутого на вектора .

Опр.:

- объём поверхности

Замечание:

Это определение имеет смысл, если область измерима по Жордану.

Пример 1:

Пример 2:

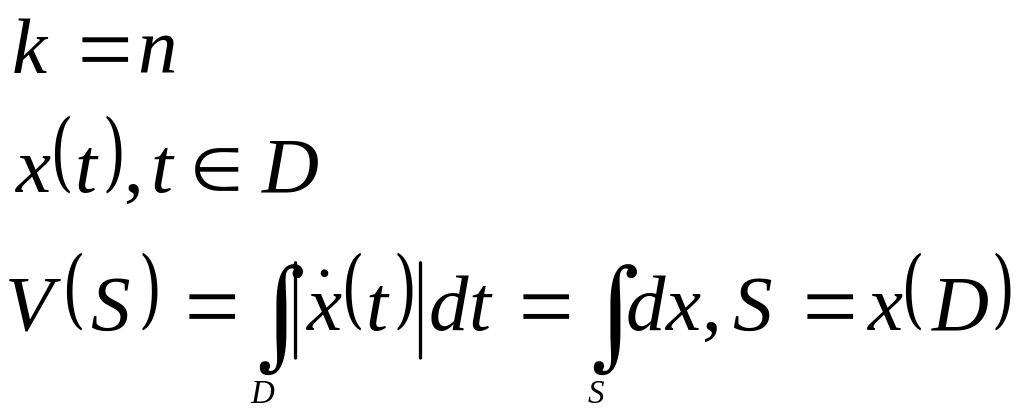
Опр.:

- -мерная поверхность

1.

2.

Утв.:

Если: - кусочно-гладкая поверхность

То: после удаления из конечного или счётного числа поверхностей размерности не выше, чем , распадается на конечное число гладких поверхностей.

Пример:

После удаления из куба рёбер и вершин, он распадается на 6 гладких поверхностей.

Опр.:

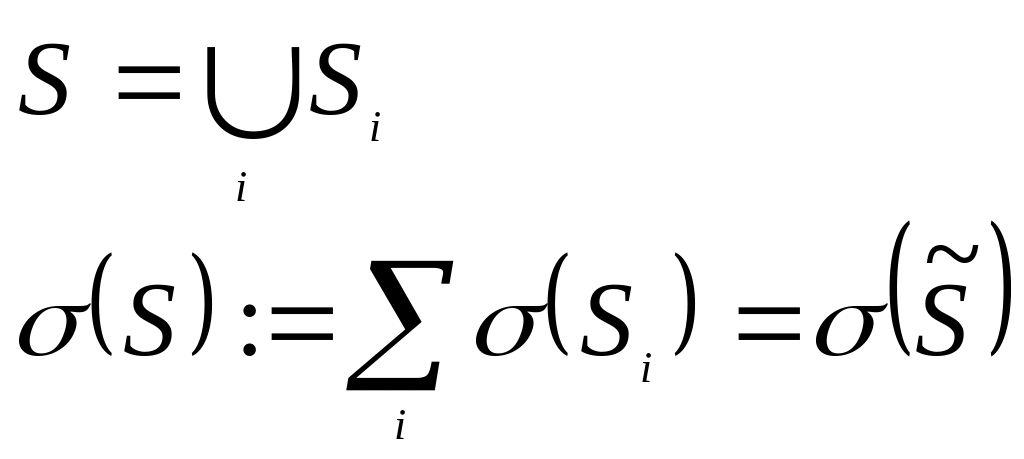
Замечание.

Если из поверхности удалить множество меры ноль, то площадь не изменится, но полученную поверхность возможно можно будет задать одной локальной картой.

Утв.:

Если:

То:

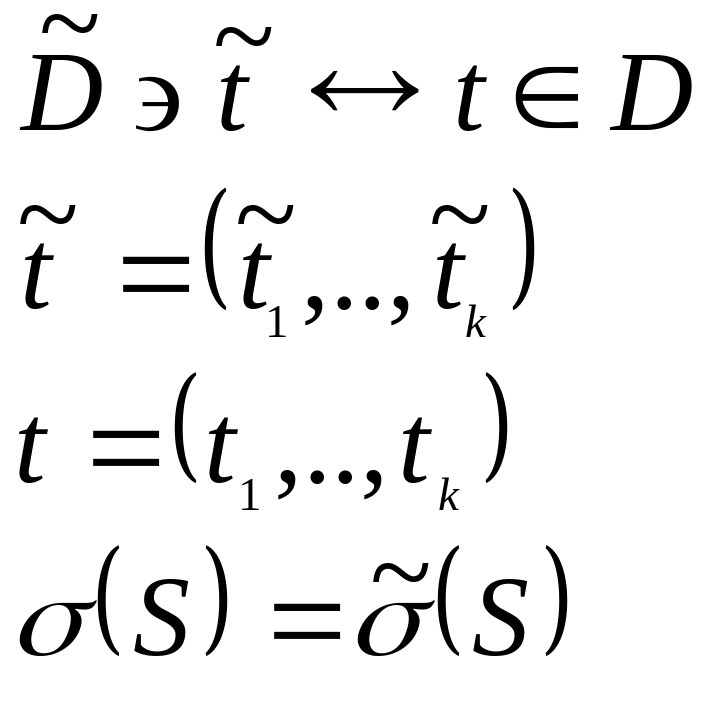
Док-во:

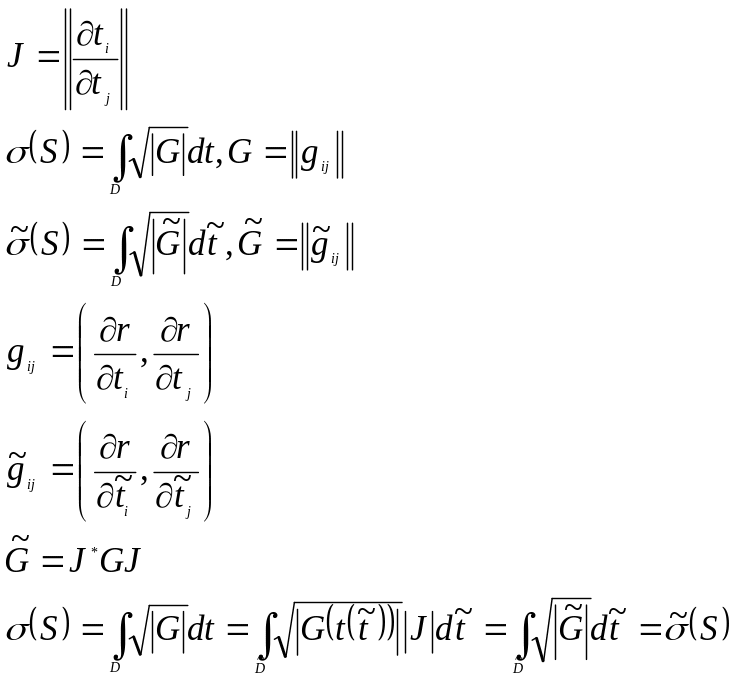
Лекция 10

Площадь поверхности в

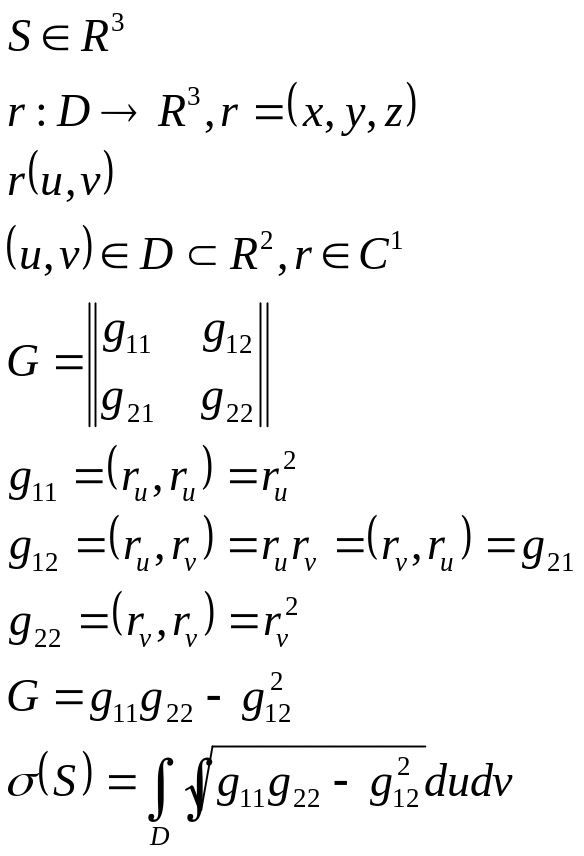
Если:

То:

Первая квадратичная форма поверхности

- касательные к координатным линиям

- касательный вектор к поверхности

Опр.:

- первая квадратичная форма поверхности.

Утв.:

1)

2) Если:

То:

Док-во:

1) очевидно

2)

используем тождество Лагранжа

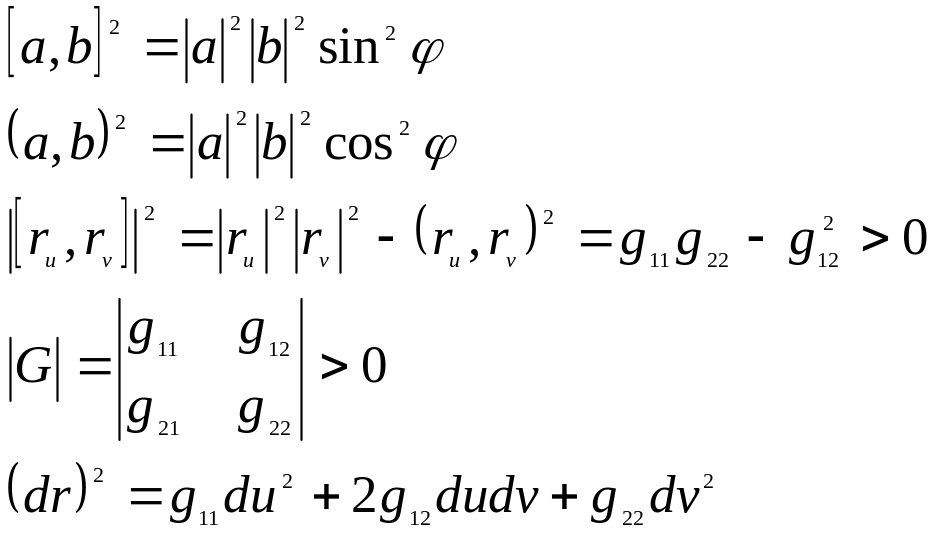
Следствие:

Пример: тор

получаем исключением и .

;

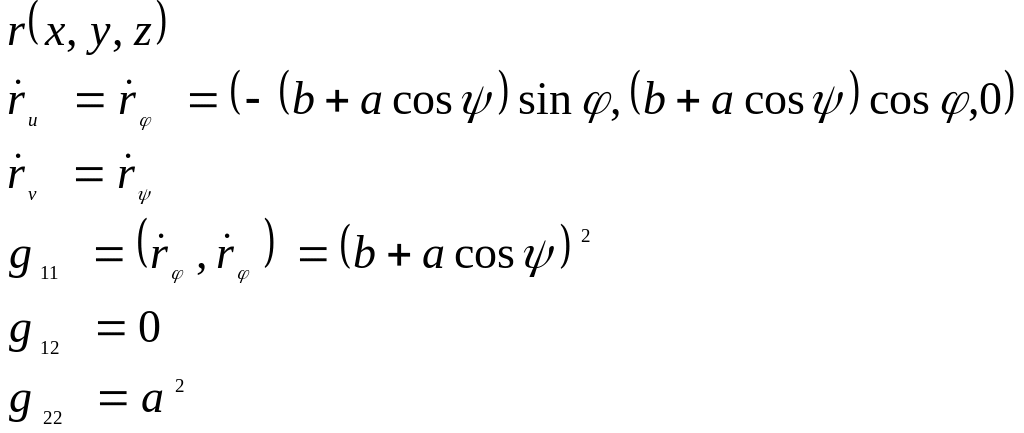
Длина кривой на поверхности

Опр.:

- поверхность

- гладкая кривая, лежащая на

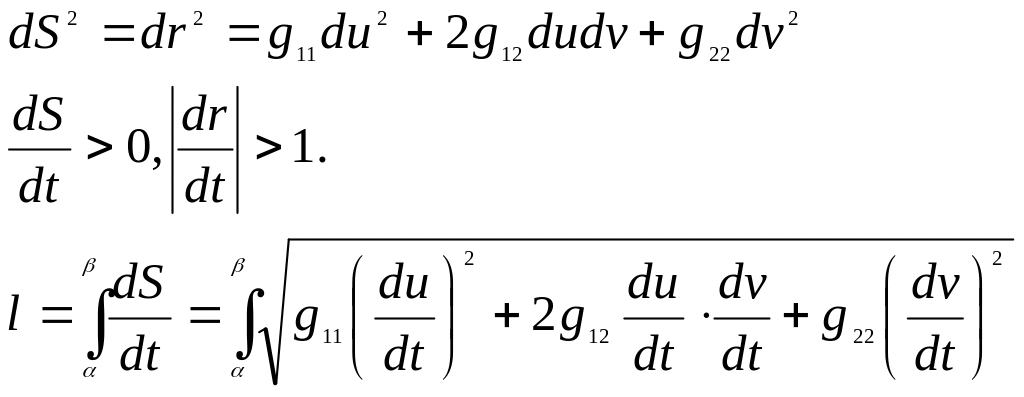
- длина кривой .

Лекция 11

Глава 3. Дифференциальные формы в

3.1. Алгебра форм

Опр.:

Если: - линейное пространство

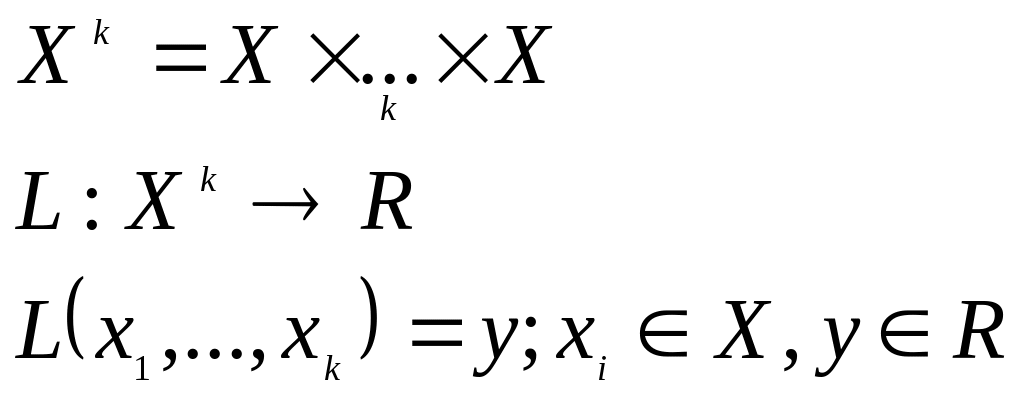
То:

1. называется формой размерности (формой, тензором), если она является полилинейной формой, т.е. формой, линейной относительно каждого аргумента:

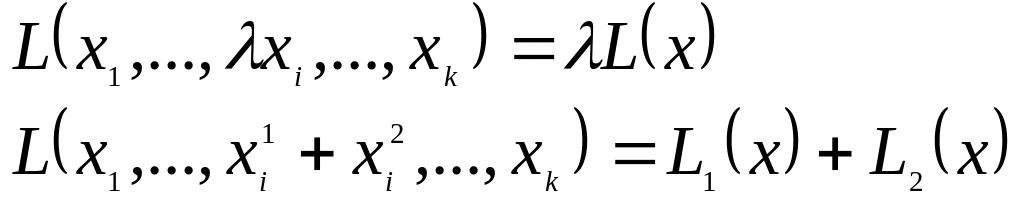
2. при называется линейной формой.

при - билинейной

Пример:

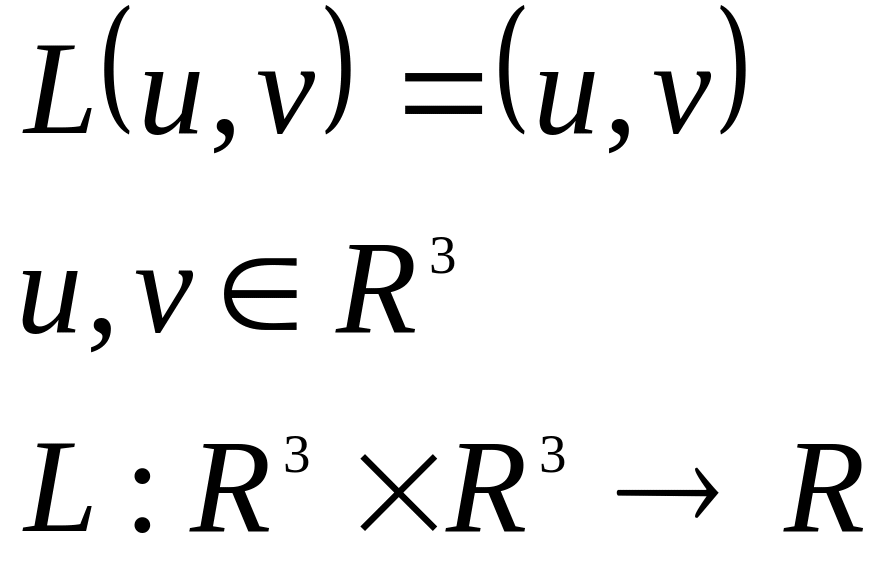
Опр.1:

- конечномерное

- базис в

Опр.2:

Утв.:

Если: -форма

- базис

То: (т.е. форма однозначно определяется набором чисел ).

Док-во:

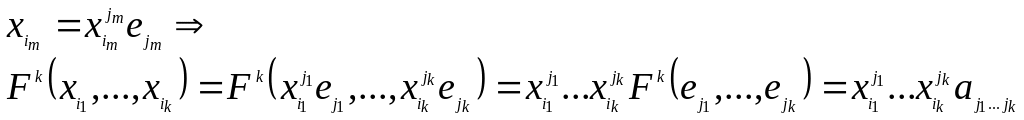
Замечание:

- линейное пространство

1)

2)

- -форма

Опр.:

- формы

операция называется тензорным произведением.

Свойства:

1.

2.

3.

Замечание

Множество всех -форм на линейном пространстве является градуированной алгеброй.

Опр.:

Если: -формы

- линейное пространство

- множество линейных функций , определённых на

То: называется пространством, сопряжённым пространству .

Опр.:

- базис

Базис пространства называется взаимным (сопряженным) базису , если:

Утв.:

Если: - базис

- сопряженный ему базис

То:

Док-во:

Опр.:

оператор называется оператором проектирования

Лекция 12