Несобственные кратные интегралы от неотрицательных функций
Теорема 2. Если:
,
- последовательность, монотонно
исчерпывающая
(
),
.
То:
Этот предел существует (конечный, либо бесконечный) и не зависит от выбора последовательности .
Док-во: Возьмём две последовательности, исчерпывающие :
и
.
1)
- покрытие компакта системой открытых
множеств.
Выделим конечное подпокрытие:
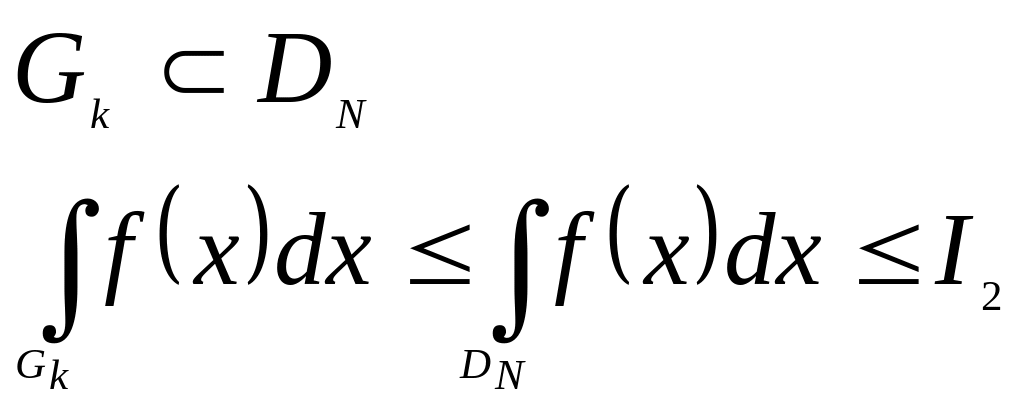
переходим к пределу при
:
2) Аналогично получаем, что
.
3) Из 1) и 2)
.
Признаки сравнения
Утверждение 1. Если: .
То:
сходится
сходится,
расходится
расходится.
Эталоны сравнения
Утверждение 2. Если:
.
То:
сходится при
сходится при
.
Док-во:
переходим к новым координатам (наподобие
полярных)
- углы
- сходится при
.
Интеграл Пуассона
Утверждение 3.
- интеграл Пуассона.
Док-во:
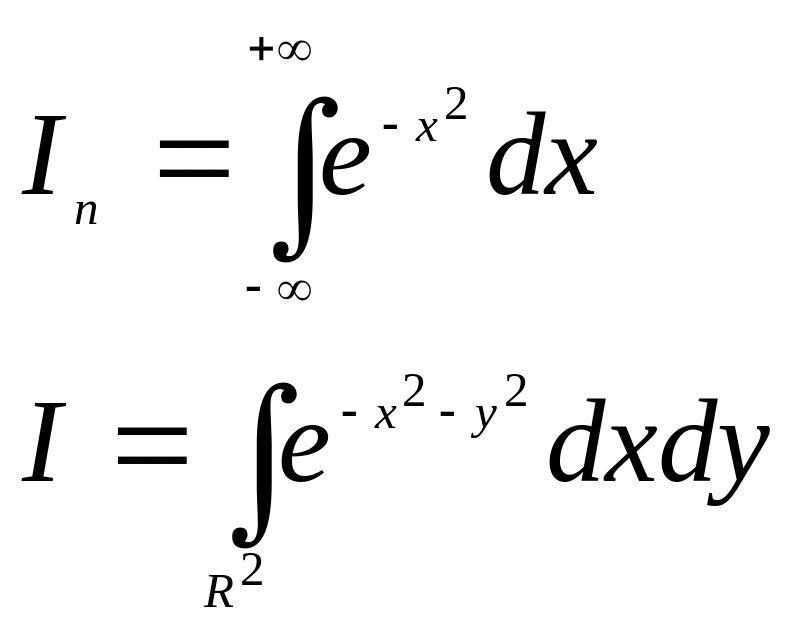
1)
2)
3)
.
Лекция 6
Глава 2. Дифференциальная геометрия
2.1 Кривые в
Векторная функция скалярного аргумента
Определение 1.
1.
- векторная функция скалярного аргумента;
2.
,
;
3.
- кусочно гладкая, когда
- кусочно гладкие.
4. Отображение - путь. Образ при отображении - носитель пути (параметризованная кривая)
Свойства предела
1.
2.
Свойства производной
Определение 2.
- скорость
1.
2. Если:
,
- скалярная функция,
- векторная,
То:
Лемма 1. Если:
- дифференцируема,
То:
.
Док-во:
Следствие 1. Если точка движется по сфере, то скорость направлена по касательной к сфере.
Определение 3.
- путь.
Если - биекция, ,
,
то
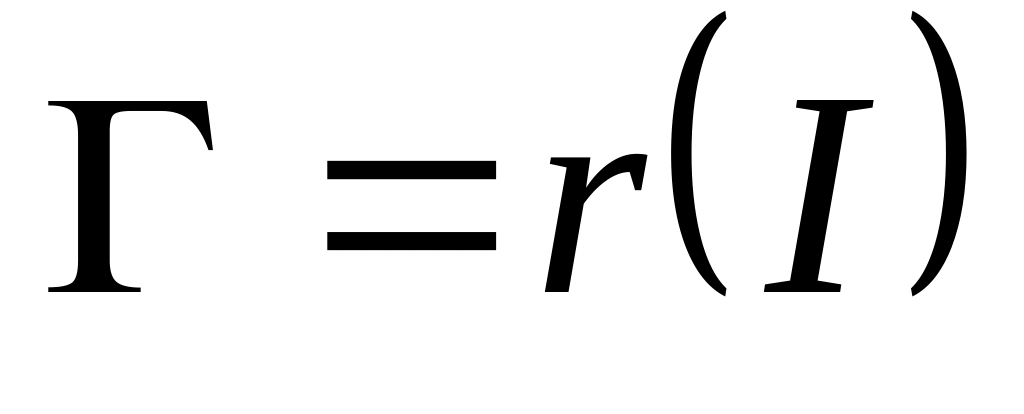- кривая (носитель пути).Гладкость кривой определяется гладкостью функций .
Касательная к кривой
Определение 4. Если:
,
то касательная в точке
имеет вид:
или
- в векторной форме
Или в координатной форме:
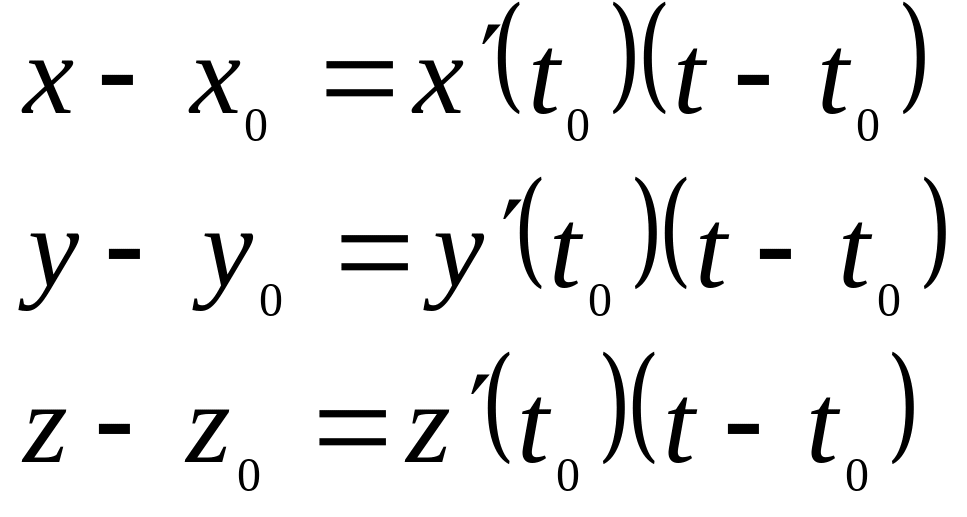
или
.
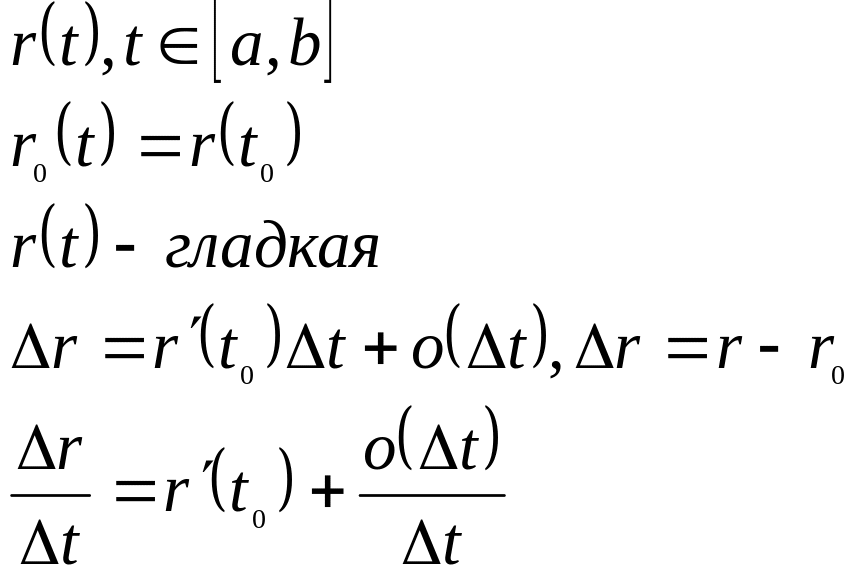
- секущая прямая
Определение 5. Предельное положение вектора секущей задаёт касательный вектор (вектор скорости).
Прямую проходящую в направлении вектора
скорости через заданную точку
называется касательной прямой к данной
кривой в данной точке.
- секущий вектор касательной
Длина кривой. Спрямляемая кривая. Натуральная параметризация
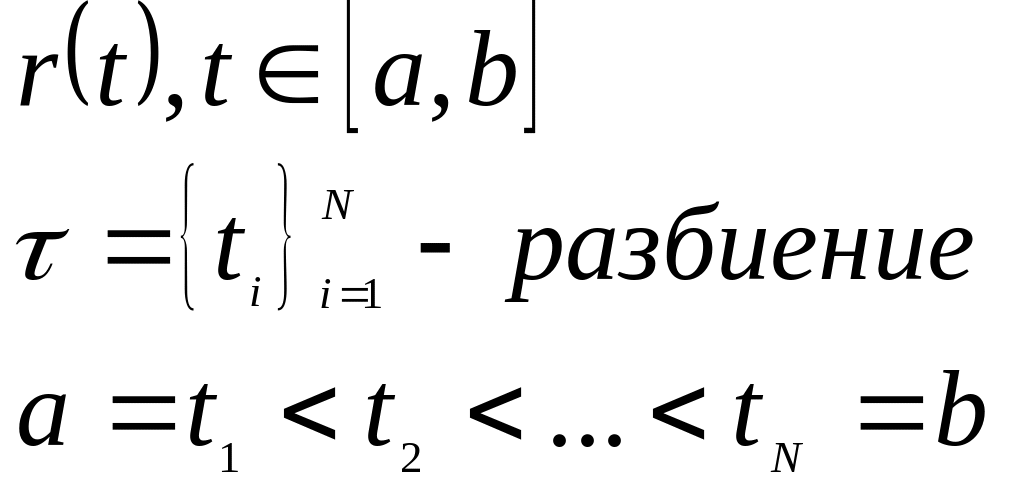
- длина ломаной
- длина кривой.
Определение 7. Если длина кривой
конечна,
то кривая называется спрямляемой.
Утверждение 1.
.
Следствие 1.
Если:
,
на
.
То:
,
Док-во:
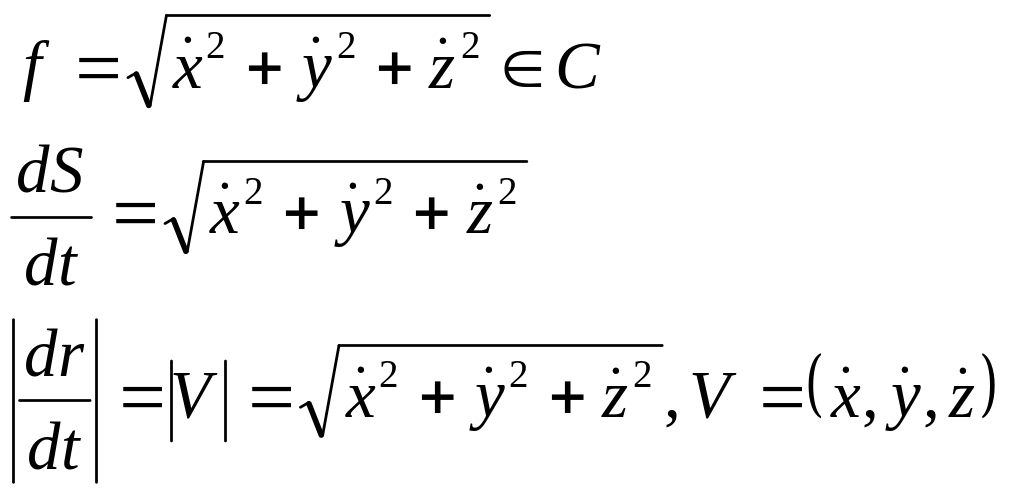
Определение 8. Натуральная параметризация – параметризация, при которой в качестве параметра используется - длина кривой от начала до данной точки.
Замечание 1.
Здесь и далее:
Следствие 2.
.
Док-во:
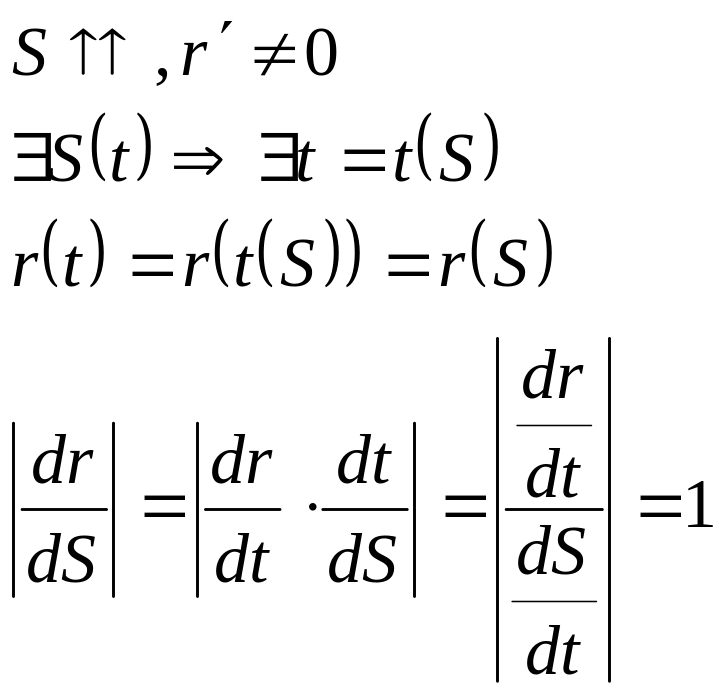
Основной трёхгранник кривой. Формулы Френе
Определение 9.
1.
- касательный вектор;
2.
- вектор нормали;
3.
.
Свойства:
1.
(т.к.
)
2.
(т.к.
и
)
3.
- правая тройка
Замечание 1.
и
- тоже правые тройки.
Определение 10. Система координат называется сопровождающей системой координат.
Определение 11.
1. Плоскость
называется нормальной.
2. Плоскость
- соприкасающаяся.
3. Плоскость
- спрямляющая.
Трёхгранник из плоскостей называется основным трёхгранником кривой.