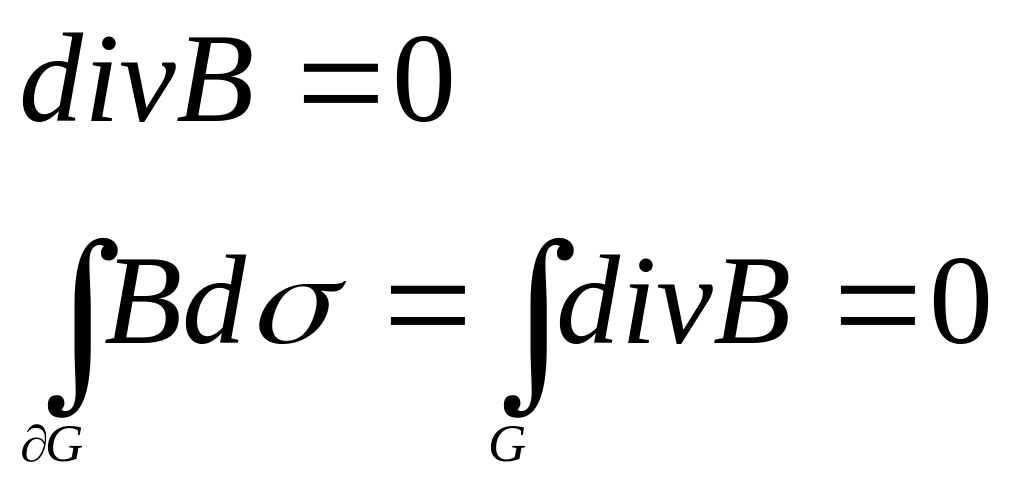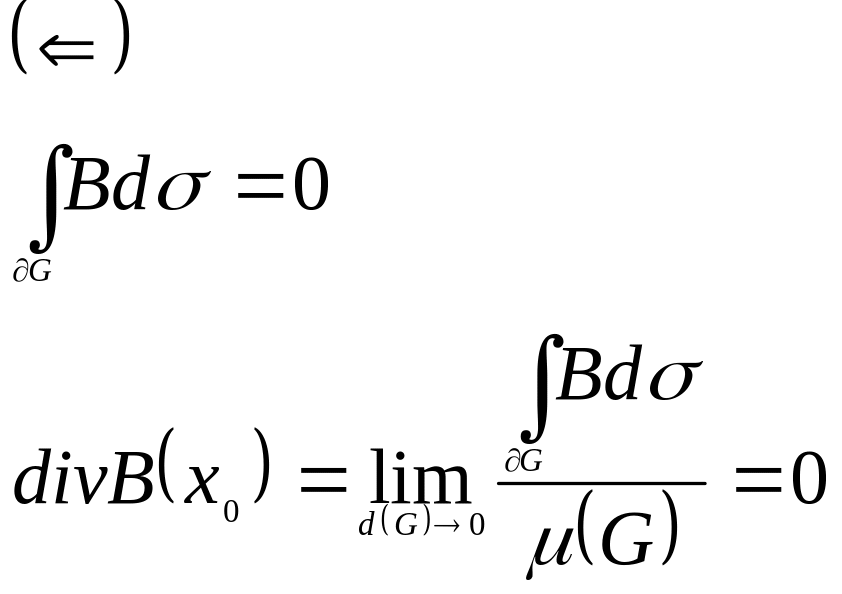- •Глава 2. Дифференциальная геометрия 15
- •1.1. Интеграл Римана на n-мерном промежутке
- •Кратный интеграл.
- •Теорема 1. Необходимое условие интегрируемости по Риману
- •Мера Лебега
- •Критерий Дарбу интегрируемости функции по Риману. Верхние и нижние суммы Дарбу.
- •Лекция 2
- •1.2. Интеграл по множеству. Допустимые множества
- •Общие свойства интеграла
- •Линейность
- •2. Аддитивность
- •3. Оценка интеграла
- •Лекция 3 Сведение кратного интеграла к повторному. Теорема Фубини
- •Замена переменных в кратном интеграле. Формула Грина.
- •Лекция 4 Геометрический смысл модуля якобиана отображения
- •1.3. Приложения кратных интегралов
- •Лекция 5
- •1.4. Несобственные кратные интегралы
- •Несобственные кратные интегралы от неотрицательных функций
- •Касательная к кривой
- •Длина кривой. Спрямляемая кривая. Натуральная параметризация
- •Основной трёхгранник кривой. Формулы Френе
- •Формулы Френе.
- •Геометрический смысл величин k и æ
- •Вид кривой вблизи произвольной точки
- •2.2. Поверхность в Евклидовом пространстве
- •Ориентация поверхности.
- •Край поверхности и его ориентация.
- •Согласование ориентации поверхности и её края
- •Касательное пространство к поверхности
- •Касательная к поверхности в
- •Площадь поверхности в Евклидовом пространстве
- •Алгебра кососимметрических форм
- •3.2. Дифференциальные формы
- •Координатная запись дифференциальной формы
- •3.3. Дифференциальные операторы векторного анализа. Их связь с дифференциальными формами
- •Перенос форм при отображениях
- •Координатная запись форм, возникающих при переносе.
- •Глава 4. Криволинейные и поверхностные интегралы.
- •4.1. Интегралы от формы работы, потока. Форма объёма
- •4.2. Интегралы I и II рода.
- •Общая формула Стокса
- •Глава 5. Элементы векторного анализа
- •5.1. Дифференциальные операции векторного анализа
- •5.2. Потенциальные поля
- •Замкнутые и точные формы
- •5.3. Соленоидальные поля
5.2. Потенциальные поля
Опр.:
1. - векторное поле в
![]() называется потенциалом поля
в
,
если
называется потенциалом поля
в
,
если
![]()
2. Поле, имеющее потенциал, называется потенциальным.
Необходимое условие потенциальности:
Утв.:
![]()
Док-во:

Утв.:
![]()
Док-во:
![]()
Утв.:
![]()
Замечание: Необходимое условие не является достаточным.
Пример:
![]()
![]()
Критерий потенциальности:
Непрерывное векторное поле
потенциально в области
![]()
![]() (циркуляция поля
вдоль любого замкнутого контура
(циркуляция поля
вдоль любого замкнутого контура
![]() равна нулю)
равна нулю)
Док-во:
![]()
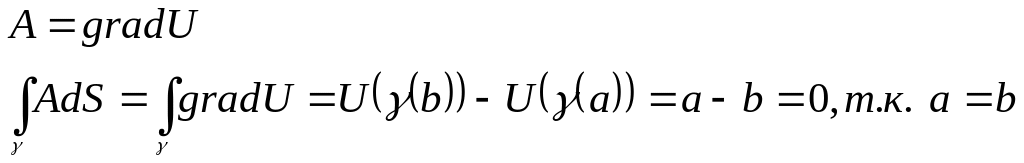


![]()
![]()
![]()
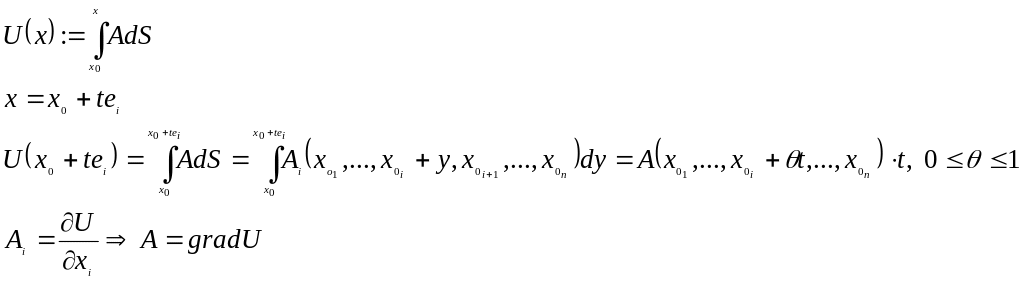
Топологическая структура области и потенциал:
Область
называется односвязной, если
замкнутого контура
![]() кусочно-гладкая ориентированная
поверхность
кусочно-гладкая ориентированная
поверхность
![]() .
.
Утв.:
Если: - односвязная область, - непрерывное векторное поле в .
То: Необходимое условие потенциальности является достаточным.
Док-во:
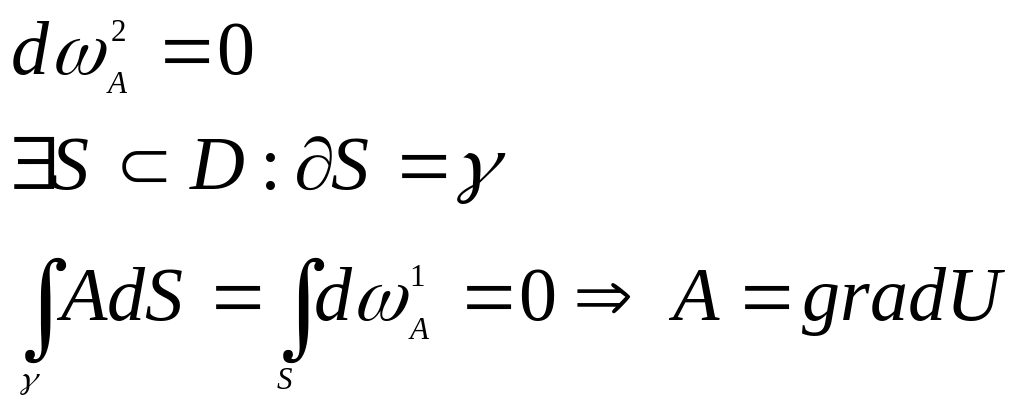
Замкнутые и точные формы
Опр.: Дифференциальная
-форма
![]() называется точной в области
,
если:
называется точной в области
,
если:
![]() .
.
Опр.: Дифференциальная
-форма
замкнута в области
,если
![]() .
.
Утв.:
Если: - точная
То: - замкнутая
Док-во:
![]()
Лемма Пуанкаре.
Если: дифференциальная форма замкнута в шаре
То: она точна в этом шаре.
Th. Пуанкаре
Если: дифференциальная форма замкнута на стягивающемся в точку многообразии
То: она точна на нём.
5.3. Соленоидальные поля
Опр.: Поле
называется векторным потенциалом поля
в области
,
если
![]()
Опр.: Поле
называется соленоидальным, если
![]() .
.
![]()
Th. Необходимое и достаточное условие соленоидальности поля:
Поле в области соленоидально
![]()
- кусочно-гладкая,
![]()
Док-во: