1. 2. Полигон частот. Выборочная функция распределения и гистограмма

Для наглядного представления о поведении исследуемой случайной величины в выборке можно строить различные графики. Один из них – полигон частот: ломаная, отрезки которой соединяют точки с координатами (x₁, n₁), (x₂, n₂),…, (x_k, n_k), где x_i откладываются на оси абсцисс, а n_i – на оси ординат. Если на оси ординат откладывать не абсолютные (n_i), а относительные (w_i) частоты, то получим полигон относительных частот (рис.1). Рис. 1.

По аналогии с функцией распределения случайной величины можно задать некоторую функцию, относительную частоту события X < x.

Выборочной (эмпирической) функцией распределения называют функцию F*(x), определяющую для каждого значения х относительную частоту события X < x. Таким образом,

, (1)

где п_х – число вариант, меньших х, п – объем выборки.

Замечание. В отличие от эмпирической функции распределения, найденной опытным путем, функцию распределения F(x) генеральной совокупности называют теоретической функцией распределения. F(x) определяет вероятность события X < x, а F*(x) – его относительную частоту. При достаточно больших п, как следует из теоремы Бернулли, F*(x) стремится по вероятности к F(x).

Из определения эмпирической функции распределения видно, что ее свойства совпадают со свойствами F(x), а именно:

0 ≤ F*(x) ≤ 1.
F*(x) – неубывающая функция.
Если х₁ – наименьшая варианта, то F*(x) = 0 при х≤ х₁; если х_к – наибольшая варианта, то F*(x) = 1 при х > х_к .

Для непрерывного признака графической иллюстрацией служит гистограмма, то есть ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высотами – отрезки длиной n_i /h (гистограмма частот) или w_i /h (гистограмма относительных частот). В первом случае площадь гистограммы равна объему выборки, во втором –

единице. 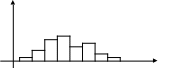Рис.2.

Пример. Дана выборка, вариационный ряд которой имеет вид:

10,8; 11,1; 11,7; 12,2; 13,1; 13,4; 13,9; 14,3; 14,3; 14,4; 14,8; 16,5; 17,7; 18,2; 19,9; 20,0; 20,3; 20,8; 23,1; 24,2; 25,1; 25,1; 25,7; 28,4; 28,5; 29,3; 29,8; 29,9; 30,2; 30,4.

Составить статистический ряд распределения абсолютных и относительных частот, состоящий из пяти интервалов, и построить гистограмму относительных частот.

Объем выборки п = 30. Выберем в качестве границ интервала а = 10,5 и b = 30,5. Тогда и (a, b) разбивается на части (10,5; 14,5), (14,5; 18,5), (18,5; 22,5), (22,5; 26,5) и (26,5; 30,5). Статистический ряд при этом имеет вид:

Номер интервала	Границы интервала	Абсолютные частоты	Относительные частоты
1	10,5; 14,5	10
2	14,5; 18,5	4
3	18,5; 22,5	4
4	22,5; 26,5	5
5	26,5; 30,5	7

Построим гистограмму:

x ◄

Пример. Выборочно обследовано 26 предприятий лёгкой промышленности по валовой продукции. Получены следующие результаты в млн. руб.: 15,0; 16,4; 17,8; 18,0; 18,4; 19,2; 19,8; 20,2; 20,6; 20,6; 20,6; 21,3; 21,4; 21,7; 22,0; 22,2; 22,3; 22,7; 23,0; 24,2; 24,2; 25,1; 25,3; 26,0; 26,5; 27,1. Составить интервальное распределение выборки с началом х₁=15 и длинами частичных интервалов h=2,5. Построить гистограмму частот.

Для составления интервального распределения составим таблицу. В первой строке расположим в порядке возрастания интервалы, длина каждого из которых h=2,5. Во второй строке запишем количество значений признака в выборке, попавших в этот интервал (т.е. сумму частот вариант, попавших в соответствующий интервал). Интервальный статистический ряд таков:

(x_i, x_i+1)	15–17,5	17,5–20	20–22,5	22,5–25	25–27,5
n_i	2	5	10	4	5

Объем выборки n=2+5+10+4+5=26. Для построения гистограммы частот на оси абсцисс откладываем частичные интервалы; на каждом из них строим прямоугольники высотой