
- •Элементы комбинаторики, размещения, перестановки, сочетания.
- •3.Пространство элементарных событий. Классическое определение вероятности
- •4.Геометрическая вероятность. Задача о встрече
- •5.Действия над событиями. Диаграммы Венна.
- •6. Теорема сложения вероятностей. Вер-ть разности двух событий
- •8.Условная вероятность.Теорема умножения вероятностей для двух событий
- •11.Формула Байеса
- •12.Повторные независимые испытания. Формула Бернулли. Наивероятнейшее число успехов
- •14.Редкие события. Теорема Пуассона
- •19.Функция распределения св и ее свойства
- •21.Функции распределения нсв. Плотность распределения вероятностей и ее свойства
- •22.Математическое ожидание дсв и нсв, его свойства и геометр.Смысл
- •23.Дисперсия св и ее свойства. Среднее квадратическое отклонение
- •24.Биноминальный закон распределения. Мат.Ожидание и дисперсия св, распределенной по биноминальному закону
- •25.Закон распределения Пуассона. Мат ожидание и дисперсия св, распределенной по закону Пуассона.
- •26.Поток событий. Простейший пуассоновский поток
- •27.Равномерное распределение. Мат ожидание и дисперсия св, распределенной равномерно
- •28.Показательный закон распределения. Мат ожидание и дисперсия св, распределенной по показательному закону.
- •29.Нормальный закон распределения. Мат ожидание и дисперсия св, распределенной по нормзакону. Влияние параметров a и на вид нормальной кривой.
- •30Выражение функции распределения норм величины через ф Лапласа. Вероятность попадания значения норма св в заданный интервал, правило трех сигм.
- •31.Неравенства Маркова.
- •32.Неравенства Чебышева.
- •33.Закон больших чисел в форме теоремы Чебышева.
- •34.Теорема Бернулли.
- •35.Понятие о центральной предельной теореме.
- •38. Эмперическая функция и эмперическая плотность распределения.
- •39. Основные числовые характеристики вариационных рядов. Среднее арифметическое и выборочная дисперсия и их свойства.
38. Эмперическая функция и эмперическая плотность распределения.
Эмп. ф-цией распределения – ф-ция, значения которой в точке х равно накопленной частоте, т.е. Fn(x)=wx=mx/n
Для
интервального ряда указываются не
конкретные значения вариант, а только
их частоты на интервалах. В этом случае
эмпирич. ф-я распределения определена
только на концах интервалов. Ее можно
изобразить ломаной, проходящей через
точки (ai,Fn(ai)),
i=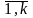
Эмпирическая плотность распр-я непрерывного вар. ряда – ф-я
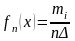 ,
если ai
≤ x≤
ai+1,
i=
;
или =0, если x<a
или x>ak+1.
,
если ai
≤ x≤
ai+1,
i=
;
или =0, если x<a
или x>ak+1.
Ф-я fn является аналогом плотности распределения случайной величины(площадь области под графиком равна
39. Основные числовые характеристики вариационных рядов. Среднее арифметическое и выборочная дисперсия и их свойства.
Средняя арифметическая (выборочное среднее): для дискретного выборочного ряда:
 ,
,
для
интервального ряда
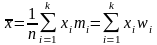 ,
где xi
- середина i-го
интервала.
,
где xi
- середина i-го
интервала.
Свойства средней арифметической:
1)если
xi
= с, то
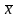 =
с; 2)
=
с; 2)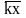 = k
= k ;
;
3)
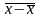 =
0; 4)
=
0; 4)
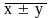 =
±
=
±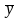 ;
;
Вариационный размах R: R=xmax-xmin.
Ср. лин. отклонение
d
= .
.
Выборочная
дисперсия-
мера рассеивания-средняя арифметическая
квадратов отклонений вариант от их
выборочной средней: S2=
Св-ва выборочной дисперсии:1)Дисперсия постоянной равна нулю;2)Если ко всем вариантам добавить постоянное число, то дисперсия не изменится;3)Если все варианты умножить на одно и то же число k, то дисперсия умножится на k2;
