
- •Элементы комбинаторики, размещения, перестановки, сочетания.
- •3.Пространство элементарных событий. Классическое определение вероятности
- •4.Геометрическая вероятность. Задача о встрече
- •5.Действия над событиями. Диаграммы Венна.
- •6. Теорема сложения вероятностей. Вер-ть разности двух событий
- •8.Условная вероятность.Теорема умножения вероятностей для двух событий
- •11.Формула Байеса
- •12.Повторные независимые испытания. Формула Бернулли. Наивероятнейшее число успехов
- •14.Редкие события. Теорема Пуассона
- •19.Функция распределения св и ее свойства
- •21.Функции распределения нсв. Плотность распределения вероятностей и ее свойства
- •22.Математическое ожидание дсв и нсв, его свойства и геометр.Смысл
- •23.Дисперсия св и ее свойства. Среднее квадратическое отклонение
- •24.Биноминальный закон распределения. Мат.Ожидание и дисперсия св, распределенной по биноминальному закону
- •25.Закон распределения Пуассона. Мат ожидание и дисперсия св, распределенной по закону Пуассона.
- •26.Поток событий. Простейший пуассоновский поток
- •27.Равномерное распределение. Мат ожидание и дисперсия св, распределенной равномерно
- •28.Показательный закон распределения. Мат ожидание и дисперсия св, распределенной по показательному закону.
- •29.Нормальный закон распределения. Мат ожидание и дисперсия св, распределенной по нормзакону. Влияние параметров a и на вид нормальной кривой.
- •30Выражение функции распределения норм величины через ф Лапласа. Вероятность попадания значения норма св в заданный интервал, правило трех сигм.
- •31.Неравенства Маркова.
- •32.Неравенства Чебышева.
- •33.Закон больших чисел в форме теоремы Чебышева.
- •34.Теорема Бернулли.
- •35.Понятие о центральной предельной теореме.
- •38. Эмперическая функция и эмперическая плотность распределения.
- •39. Основные числовые характеристики вариационных рядов. Среднее арифметическое и выборочная дисперсия и их свойства.
30Выражение функции распределения норм величины через ф Лапласа. Вероятность попадания значения норма св в заданный интервал, правило трех сигм.
1) Распределение
N(0;1)
наз-ся станд-ным нормальным..Для
стандартного распред-я плотность вер-ти
равна:
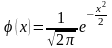 ,
а ф-я распред-я
,
а ф-я распред-я
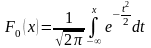 .
.
Ф-я Лапласа
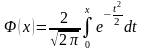 и ф-я распред-я НСВ Х
с параметрами
и ф-я распред-я НСВ Х
с параметрами
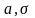 связаны соотнош-м:
связаны соотнош-м:
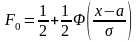 .
.
2)Получим формулу
д/вычисления вер-ти попадания НСВ с
параметрами
в
задан. интервал(α;β) через стандарт-е
распред-е
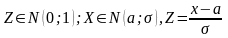 :
: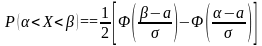
3)3σ
Вер-ть того,
что НСВ отклоняется от своего мат.ожид-япо
модулю меньше, чем ε>0, определяется
формулой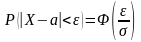 .
Если положить
.
Если положить
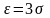 ,
то получим
,
то получим
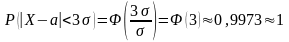 .
.
Отсюда вытекает,
что среди 10000 значений НСВ в среднем
только 27 выйдут за пределы интервала
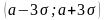 .
Это означает, что практически среди
небольшого числа значений Х нет таких,
кот. выходят за пределы указанного
интервала. Правило 3-х сигм часто
применяется д/грубой оценки сигма:
.
Это означает, что практически среди
небольшого числа значений Х нет таких,
кот. выходят за пределы указанного
интервала. Правило 3-х сигм часто
применяется д/грубой оценки сигма:
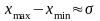 .
.
31.Неравенства Маркова.
Теорема: Пусть Св Х принимает только неограниченное значение α- любое положительное число тогда вероятность того что СВ х≥0 ¥ α>0
P(x<α)≥1-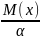 (1)
(1)
Док-во т к х≥0
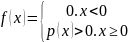
M(X)=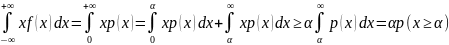
P(X≥α)≤M(X)/α
-P(X≥α)≥-M(X)/α
1-p(X≥α)≥1-M(X)/α
32.Неравенства Чебышева.
Если Х-СВ, мат. ожидание к-рой М(Х) = а, а дисперсия D(Х) конечна, то д/любого числа ε> 0 выполняются неравенства:
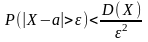
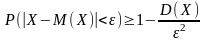
Док-во
Ιx-M(X)ι<E↔(X-M(X))2<E2
Введем новую СВ Y=(X-M(X))2≥0
M(X)=M(X_M(X))2=D(X)
P(X)<E2)≥1-M(X)/E2=1-D(X)/E2т к события РΙx-M(X)ι≥E противоположные то справедливо неравенство
РΙx-M(X)ι≥E)≤D(X)/E2
При неизв-ом з-не распред-я на практике при известных М(Х),D(X) участком возможных значений СВ Х считают М(Х)±3σ(Х)
33.Закон больших чисел в форме теоремы Чебышева.
Лемма
2 (неравенство Чебышева).
Для любой случайной величины Х,
имеющей конечную дисперсию и любого
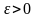
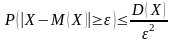 .
.
Следствие 2. Для любой случайной величины Х с конечной дисперсией и любого
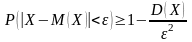
Теорема
Чебышева. Если
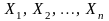 последовательность независимых
случайных величин с математическими
ожиданиями
последовательность независимых
случайных величин с математическими
ожиданиями
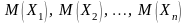 и дисперсиями
и дисперсиями
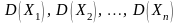 ,
ограниченными одной и той же постоянной
,
ограниченными одной и той же постоянной
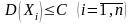 ,
то какова бы ни была постоянная
,
то какова бы ни была постоянная
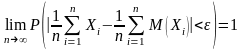 .
.
При доказательстве предельного равенства используется неравенство
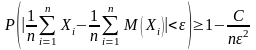 ,
,
которое вытекает из неравенства Чебышева.
34.Теорема Бернулли.
Если вероятность наступления событ А в каждом изn -_независ испыт постоянно то при неограниченном увеличении числа n –испытаний относит частота m/n –наступления событияА стремиться по вероятности к числу р т е для любого Е>0
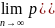 <E)=1
<E)=1
Док-во Рассм Св Х1,Х2…..Хn где Xi–число наступлений события А в i- ом испытании
хi 0 1.
рi 1-р р .
M(X)=p D(X)=pq=c
35.Понятие о центральной предельной теореме.
Закон больших чисел устанавливает факт приближения большого кол-ва СВ к определенным постоянным однако суммарные действия СВ не ограничивается только такими закономерностями
Оказывается что совокупные действия многих случ факторов СВ приводит к определнному закону распределения а именно к норм закону распред
Теорема Ляпунова
Пусть
Xi…Xn–независ
Св имеющие матем ожидание M(Xi)=aibD(X)=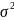 и
абсолютные центральные моменты 3-го
порядка
и
абсолютные центральные моменты 3-го
порядка
M=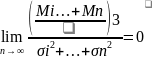 тогда
закон распред суммы Yn=X1….+Xn
неограниченно приближается к норм
закону с ростом n
с мат ожиданием N(
тогда
закон распред суммы Yn=X1….+Xn
неограниченно приближается к норм
закону с ростом n
с мат ожиданием N(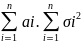 )
)
Т к для Св выполн все условия теоремы Чебышева то мы можем записать для них неравенство с cc-pq
P(ǀ ǀ<E)≥1-pq/nE2
ǀ<E)≥1-pq/nE2
P(ǀm/n-np/nǀ)<E)≥1-pq/nE2
36.Генеральная и выборочная совокупности. Дискретный вариационный ряд и его графические изображения.
Мат. Ст-ка занимается установлением закономерностей, к-рым подчинены массовые случайные явления, на основе обработки стат. данных, полученных в результате наблюдений.
Генеральная совокупность – все множество имеющихся объектов. Выборка – набор объектов, случайно отобранных из генеральной совокупности. Объем генеральной совокупности N и объем выборки n – число объектов в рассматривае-мой совокупности.
Виды выборки: повторная и бесповторная. Выборка должна правиль-но представлять пропорции ген.сов-сти, то есть быть репрезентативной (представительной). Учитывая закон больших чисел, можно утверждать, что это условие выполняется, если каждый объект выбран случайно, причем д/любого объекта вероятность попасть в выборку одинакова.
Вариационный ряд наз-ся ряд вариант расположенных в порядке возрастания вместе с соответствующими весами если изуч.ДСВ то ДВР.
Полигон –ломаная соединяющая точки плоскости с координатами (х,mi)
Кумулянта- ломаная соед точки плос-ти с корд-ми(x,mxi)
Гистограмма –для изобр.вар.рядов и имеют вид ступ фигурыиз прямоуг.с основ.=длина инт-ла и высотами=частотам.
37.Интервальный вариационный ряд и его графические изображения.
Интервальный ряд –ряд, представляющий собой выборку непрерывной случ велечины.
Для построения интер. Вар. Ряда разбивают множество значений вариант на полуинтервалы [ак, ак=1], т.е. проводят группировку.
Для определения оптим. велечины интервала используют формулу Стерджерса: h=(xmax-xmin)/( 1+3,332ln n).
Для графического представления интер.вар. ряда используется гистрограмма – ступенчатая фигура, состоящая из прямоугольников, основанием для которых служат частичные интервалы, а высоты – частоты или частости.
