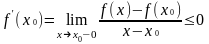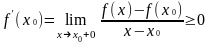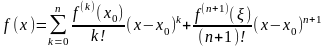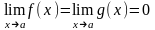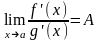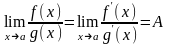- •Множества и действия над ними.
- •Понятие отображения, образ и прообраз множества при отображении, суперпозиция отображений, сужение отображения, график отображения.
- •Сюрьективные, инъективные и биективные отображения. Обратное отображение.
- •Аксиома непрерывности множества вещественных чисел. Точные грани числовых множеств.
- •10. Число e.
- •11. Бесконечно малые и бесконечно большие последовательности.
- •12. Лемма о вложенных отрезках.
- •18. Локальные свойства функций имеющих предел.
- •16. Предел функции: два определения и их эквивалентность. Теоремы о пределе функции, вытекающие из теорем о пределе числовой последовательности
- •21. Бесконечные пределы и пределы в бесконечности.
- •19.Теорема о пределе суперпозиции
- •23. Символы о-малое и о-большое, эквивалентные б.М. И б.Б.
- •24. Замечательные пределы
- •27. Точки разрыва функции и их классификация. Примеры: функция Дирихле и другие примеры
- •29. Теоремы Больцано-Коши о промежуточных значениях непрерывной функции.
- •30. Теоремы Вейерштрасса о непрерывных на отрезке функциях
- •Д о к а з а т е л ь с т в о. Достаточно заметить, что
- •33. Дифференцируемые функции. Понятие дифференциала
- •46. Условия монотонности функции.
- •47. Условия экстремума функции.
- •48. Условия выпуклости функции
- •51.Комплексные числа
- •14. Частичные пределы. Верхний и нижний пределы.
- •13. Подпоследовательности. Теорема Больцано-Вейерштрасса об ограниченной последовательности.
- •28. Равномерно непрерывные функции. Теорема Кантора.
- •40. Производные и дифференциалы высших порядков.
- •39. Теоремы о среднем значении для дифференцируемых функций: теоремы Роля, Лагранжа и Коши.
Д о к а з а т е л ь с т в о. Достаточно заметить, что

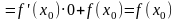 □
□
Геометрический
смысл производной. Производная
функции
в точке
– тангенс угла наклона касательной к
графику этой функции в точке
 (подробнее на лекции и в учебниках
(подробнее на лекции и в учебниках
Физический
смысл производной Если функция
( )
описывает закон изменения одной
физической величины
в зависимости от изменения другой
физической величины
,
то производная
часто называется скоростью изменения
первой из этих величин относительно
второй, причем эта скорость порой имеет
специальное название: сила тока,
плотность вещества, ускорение
)
описывает закон изменения одной
физической величины
в зависимости от изменения другой
физической величины
,
то производная
часто называется скоростью изменения
первой из этих величин относительно
второй, причем эта скорость порой имеет
специальное название: сила тока,
плотность вещества, ускорение
33. Дифференцируемые функции. Понятие дифференциала
Пусть функция определена в окрестности точки .
Определение
1.
Если существует такая линейная функция
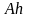 вещественного аргумента
(
вещественного аргумента
(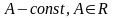 ),
что приращение
),
что приращение
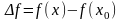 функции
может быть представлено в виде
функции
может быть представлено в виде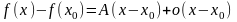
где
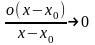 при
при
 ,то
функция
называется дифференцируемой в точке
,
а соответствующая линейная функция
аргумента
,то
функция
называется дифференцируемой в точке
,
а соответствующая линейная функция
аргумента
 называется
ее дифференциалом в этой точке.и
обозначается
называется
ее дифференциалом в этой точке.и
обозначается или
или
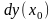 .
.
Теорема 1. Для того, чтобы функция была дифференцируемой в точке , необходимо и достаточно, чтобы она имела в этой точке конечную производную .
Геометрический
смысл дифференциала.
Нетрудно убедиться, что значение
дифференциала
 в точке
в точке
 равно приращению ординаты касательной
к графику функции
в точке
равно приращению ординаты касательной
к графику функции
в точке
 .
Подробнее об этои см. учебники Фихтенгольца
и Кудрявцева.
.
Подробнее об этои см. учебники Фихтенгольца
и Кудрявцева.
Физический
смысл дифференциала.
Если
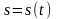 – длина пути, проходимого материальной
точкой за время
– длина пути, проходимого материальной
точкой за время
 ,
то дифференциал
,
то дифференциал
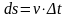 (
(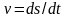 – скорость в момент времени
)
– путь, который она бы прошла за
промежуток времени
– скорость в момент времени
)
– путь, который она бы прошла за
промежуток времени
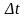 при условии, что она бы двигалась на
нем с постоянной скоростью, равной
скорости
при условии, что она бы двигалась на
нем с постоянной скоростью, равной
скорости
 в момент времени
.
Если
в момент времени
.
Если
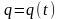 – количество электричества, протекающее
через поперечное сечение проводника
в момент времени
,
то дифференциал
– количество электричества, протекающее
через поперечное сечение проводника
в момент времени
,
то дифференциал
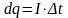 (
(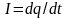 – сила тока в момент времени
)
– количество электричества, которое
протекло бы через это поперечно сечение
за время
,
точнее от момента времени
до момента времени
– сила тока в момент времени
)
– количество электричества, которое
протекло бы через это поперечно сечение
за время
,
точнее от момента времени
до момента времени
 ,
при условии, что сила тока была бы
постоянной и равнялась силе тока в
момент времени
.
,
при условии, что сила тока была бы
постоянной и равнялась силе тока в
момент времени
.
34. Арифметические операции с дифференцируемыми функциями.
Теорема. Пусть функции и определены в окрестности точки и дифференцируемы в этой точке. Тогда в этой точке дифференцируема и каждая из функций
 ,
,
,
,
 и
(при
и
(при
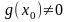 ),
),
Причем



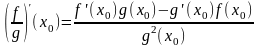
35. Дифференцирование сложной функции
Теорема.
Пусть
функция
определена на интервале
 ,
а функция
определена на интервале
,
а функция
определена на интервале
 ,
причем
,
причем
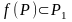 .
Тогда если функция
дифференцируема в точке
.
Тогда если функция
дифференцируема в точке
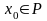 ,
а функция
дифференцируема в точке
,
а функция
дифференцируема в точке
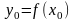 ,
то сложная функция
дифференцируема в точке
и
,
то сложная функция
дифференцируема в точке
и
36. Дифференцирование обратной функции
Теорема
3.
Пусть
функция
строго монотонна и непрерывна в
окрестности
 точки
.
Пусть,
кроме того, функция
дифференцируема в точке
и
точки
.
Пусть,
кроме того, функция
дифференцируема в точке
и
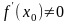 .
Тогда обратная к ней функция
дифференцируема в точке
,
причем
.
Тогда обратная к ней функция
дифференцируема в точке
,
причем
|
(1) |
37. Дифференцирование элементарных функций. Таблица производных
nо 1. Таблица производных
Элементарные
функции (за исключением функций
 и
и
 )
дифференцируемы в своих областях
определения, причем справедливы
следующие формулы (они обосновываются
в следующих пунктах):
)
дифференцируемы в своих областях
определения, причем справедливы
следующие формулы (они обосновываются
в следующих пунктах):
 .
.

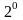 .
.

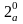 .
.
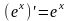
 .
.
![]()
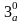 .
.

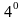 .
.
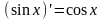
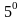 .
.
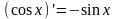
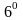 .
.
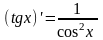
 .
.

 .
.
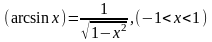
 .
.
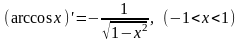
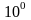 .
.
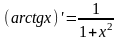
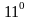 .
.

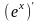 =
=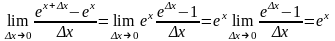
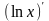 =
= .
.
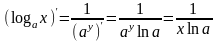
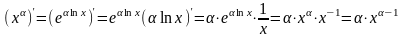
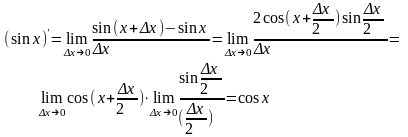
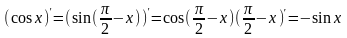
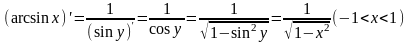
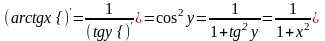
38. Локальный экстремум функции. Теорема Ферма
Определение
1. Пусть
функция
определена
на множестве
и
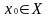 .
Говорят, что в точке
.
Говорят, что в точке
 функция
имеет локальный минимум
(локальный
максимум)
,
если существует такая окрестность
этой
точки, что
функция
имеет локальный минимум
(локальный
максимум)
,
если существует такая окрестность
этой
точки, что
|
(1) |
( |
|
при этом точку называют точкой локального минимума (локального максимума) функции.
локальный экстремум, при этом точку называют точкой локального экстремума.
всякая точка глобального экстремума является также и точкой локального экстремума
Теорема
1(Ферма).
Пусть
функция
определена на множестве
,
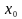 -
внутренняя точка множества
и функция
дифференцируема в этой точке .Тогда,
если
– точка локального экстремума этой
функции, то
-
внутренняя точка множества
и функция
дифференцируема в этой точке .Тогда,
если
– точка локального экстремума этой
функции, то
|
(2) |
Д
о к а з а т е л ь с т в о.
Для определенности будем считать , что
─
точка локального минимума . Тогда
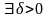 такое, что
такое, что
 (
─
внутренняя
точка
)
и
(
─
внутренняя
точка
)
и
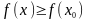
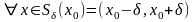 .
.
Поэтому
|
(3)
|
|
(4)
|
Из неравенства (3) , в силу дифференцируемости функции в точке и теоремы о предельном переходе в неравенстве, очевидно следует, что
|
(5)
|
а из неравенства (4) , в силу того же, в свою очередь, следует , что
|
(6)
|
из неравенств (5) и (6) и вытекает равенство (2) □
39 Формула Тейлора для многочлена
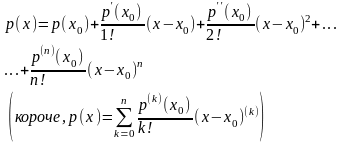 Формулу
Тейлора для многочлена
Формулу
Тейлора для многочлена
 в
точке
в
точке
 ,
то есть формулу
,
то есть формулу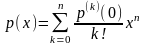 называют
также формулой Маклорена.
называют
также формулой Маклорена.
40. Локальная формула Тейлора (формула Тейлора с остаточным членом в форме Пеано).
|
(3) |
43. Формула Тейлора с остаточным членом в форме Лагранжа и в форме Коши.
(формула Тейлора с остаточным членов в форме Лагранжа),
|
|
|
|
|
|
|
(11) |
||
(формула Тейлора с остаточным членом в форме Коши)□

44. Разложение элементарных функций по формуле Тейлора
.
Пусть


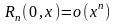 (
в
форме Пеано)
(
в
форме Пеано)
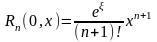 (
в
форме Лагранжа)
(
в
форме Лагранжа)
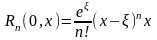 (в
форме Коши),
(в
форме Коши),
.
Пусть
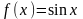
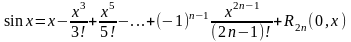
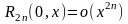 ,
,
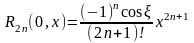
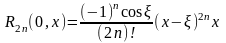
.
Пусть
 .
.


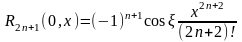
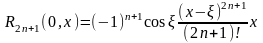
.
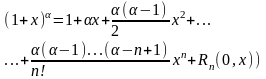
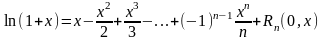

45. Правило Лопиталя
Теорема
1. Пусть
функции
и
дифференцируемы на конечном или
бесконечном интервале
 ,
, на
и
на
и
|
(1) |
Тогда если существует конечный или бесконечный предел
|
(2) |
то существует и равный ему предел , т.е.
|
(3) |
Теорема 2. Пусть функции и дифференцируемы на конечном или бесконечном интервале , на и
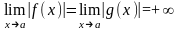 .
.
Тогда если существует конечный или бесконечный предел
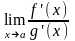 то
существует и равный ему предел
.
то
существует и равный ему предел
.



 ),
),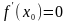 .
.
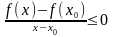
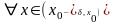
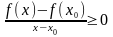
 .
.