27. Точки разрыва функции и их классификация. Примеры: функция Дирихле и другие примеры

Определение 1. Пусть функция определена на множестве и . Если функция непрерывна в точке , то она называется точкой непрерывности функции . В противном случае, точка называется точкой разрыва функции .

Определение 2. Пусть – точка разрыва функции . Если оба односторонних предела и существуют и конечны, то она называется точкой разрыва 1-го рода

Определение 3. Точка разрыва 1-го рода называется точкой устранимого разрыва функции , если в ней существует предел функции , но он не равен ее значению в этой точке.

Определение 4. Точка разрыва функции называется точкой разрыва 2-го рода, если она не является точкой разрыва 1-го рода.

Пример 1 (всюду разрывной функции). Функция Дирихле, определенная на всей числовой оси равенствами:

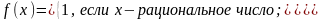
является разрывной в каждой точке .

Более того, нетрудно видеть, что

каждая точка – точка разрыва 2-го рода функции Дирихле.

29. Теоремы Больцано-Коши о промежуточных значениях непрерывной функции.

Теорема 1 (первая теорема Больцано-Коши)

Пусть функция определена и непрерывна на отрезке 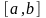( 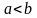) и на концах его принимает значения разных знаков (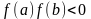 ). Тогда найдется такая точка , в которой функция обращается в нуль:

(1)

Теорема 2 (вторая теорема Больцано-Коши)

Пусть функция определена и непрерывна на отрезке , причем на концах этого отрезка она принимает разные значения

.

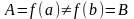Тогда каковы бы ни было число 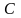, лежащее между и найдется такое , что

.Д о к а з а т е л ь с т в о. Пусть для определенности . Выберем произвольное , , и рассмотрим вспомогательную функцию 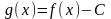. Она, очевидно, непрерывна на отрезке и на его концах принимает значения разных знаков:

По теореме 1 существует такое , что , т.е. или □

Следствие. Если функция определена и непрерывна на конечном или бесконечном промежутке 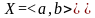, то множество ее значений 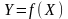также есть некоторый промежуток.

30. Теоремы Вейерштрасса о непрерывных на отрезке функциях

Теорема 1 (первая теорема Вейерштрасса). Всякая непрерывная на отрезке функция ограничена на этом отрезке.

Д о к а з а т е л ь с т в о. Предположим противное. Тога для любого натурального найдется такая точка 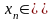, что

.

(1)

Так как последовательность ограничена (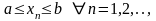 ), то по теореме Больцано-Вейерштрасса она содержит сходящуюся подпоследовательност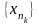ь . Пусть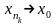 при 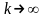.Очевидно, что 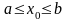(для того, чтобы убедиться в этом достаточно в неравенствах перейти к пределу при ). Поэтому в силу непрерывности функции на отрезке

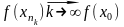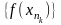Следовательно, последовательность ограничена, что, противоречит тому, что согласно (1) □

Теорема 2 (вторая теорема Вейерштрасса). Всякая непрерывная на отрезке функция достигает на нем своих точных верхней и нижней граней, т.е. существуют такие точки ,что , .

Д о к а з а т е л ь с т в о. Докажем, например, утверждение теоремы относительно точной верхней грани. Доказательство проведем от противного. А именно, положим и предположим, что .Тогда, очевидно, функция

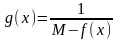
будет непрерывной на отрезке . Поэтому по теореме 1 она будет ограниченной на этом отрезке. В частности, найдется такое 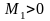, что

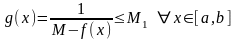Следовательно 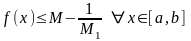,а это противоречит тому, что □

32. Понятие производной, ее геометрический и механический смысл. Уравнение касательной к графику функции в данной точке.

Пусть и . Точка называется внутренней точкой множества , если она принадлежит ему вместе с некоторой своей окрестностью, т.е. существует такая окрестность 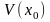точки , что .

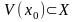Определение 1. Если существует предел 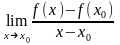то он называется производной функции в точке .

Таким образом

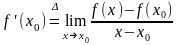
производная 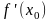равна пределу отношения приращения функции (в точке ) к приращению аргумента

Теорема 1. Пусть функция определена в окрестности точки и имеет в этой точке конечную производную. Тогда она непрерывна в этой точке.
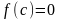
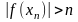