Сюрьективные, инъективные и биективные отображения. Обратное отображение.
Отображение называется
а) сюръективным
или
отображением “на”,
если
;
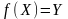b) инъективным или взаимно однозначным отображением «в», если
из того, что
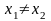следует, что
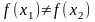(или,
равносильно, если
из того, что
следует, что
);
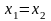в) биективным или взаимно однозначным отображением «на» или также взаимно однозначным соответствием, если оно одновременно инъективно и сюръективно.
Пусть отображение устанавливает взаимно однозначное соответствие между множествами и , т.е. является биективным. Тогда можно определить новое отображение
,
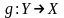полагая, что
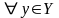его образом
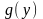при отображении
является тот единственный элемент
,
образом которого при отображении
является
соответствующий элемент
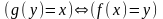Так
определенное отображение g
называется обратным
к отображению
и обозначается
,
т.е.
.
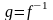Аксиома непрерывности множества вещественных чисел. Точные грани числовых множеств.
Аксиома непрерывности. Для любых непустых подмножеств и числовой прямой
,
обладающих тем свойством, что
,
существует,
по крайней мере, одно такое число
,
которое разделяет эти множества, т.е.
.
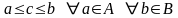Опр 1. Множество
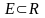называется
а)
ограниченным
сверху,
если существует такое число
, что
,при этом число
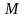назыв
верхней
гранью
множества
.
б)
ограниченным
снизу,
если существует такое число
, что
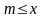,при
этом число
называется
нижней
гранью
множества
.
в) ограниченным, если оно ограничено сверху и снизу.
Лемма
1. Множество
– ограничено
.
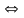
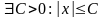Очевидно,
если M – верхняя грань (соотв., m–нижняя
грань) множества
,
то каково бы ни было
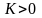число
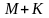также будет его верхней гранью(соотв.,
будет его нижней гранью). Поэтому
ограниченное сверху множество имеет
бесконечное число верхних граней, а
ограниченное снизу множество имеет
бесконечное число нижних граней.
Опр 3. Наименьшая из верхних граней множества называется точной верхней гранью этого множества, а наибольшая из его нижних граней называется точной нижней гранью этого множества.
Точная
верхняя грань множества
обозначается символом
,а
точная нижняя грань множества
обозначается
Лемма
2 (о
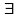точных граней). Всякое непустое,
ограниченное сверху числовое множество
имеет точную верхнюю грань, а всякое
непустое, ограниченное снизу числовое
множество имеет точную нижнюю грань
.
5.Предел числовой последовательности. Сходящиеся и расходящиеся последовательности. Единственность предела. Ограниченность сходящейся числовой последовательности.
Опр
1. Число
(точка)
называется пределом
последовательности
,
если для любого
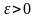существует такой номер
,
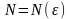что для всех натуральных
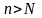имеет место неравенств
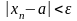.Обозначение:
,Краткое,
символическое определение:
|
В
общем случае, окрестностью
точки
называют всякое множество
,
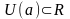которое содержит некоторую ее
-окрестность
.
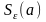Число
(точка)
называется пределом
последовательности
,
если все ее члены, начиная с некоторого
номера, принадлежат любой наперед
заданной окрестности
точки
.
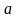Опр 2. Если числовая последовательность имеет предел, то говорят, что она сходится и называют ее сходящейся. В противном случае, т.е. если она не имеет предела, говорят, что она расходится и называют ее расходящейся.
Теорема 1. Всякая сходящаяся последовательность имеет только один предел.
Опр
3. Числовая
последовательность
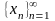называется
А)
ограниченной,
если
:
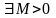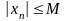
Б)
ограниченной
сверху,
если
:
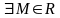В)
ограниченной
снизу,
если
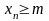
Теорема 2. Всякая сходящаяся последовательность ограничена.
6.Арифметические свойства сходящихся последовательностей.
Лемма
1. Если
последовательность
сходится и
,то
последовательность
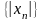также сходится и
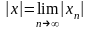(короче,
).
Выберем
.
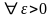Т.к.
,
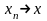то
:
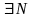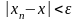
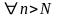,а
по свойству 5о
абсолютной величины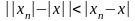
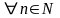,Þ
.
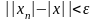В
силу произвольности выбранного
,
это и означает, что
□
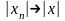Опр
1. Суммой,
разностью, произведением и частным
последовательностей
и
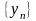называются, соответственно, следующие
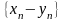последовательности:
,
,
и
,
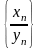для любого
.
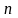Теорема 1. ⊐ последовательности и сходятся.
Тогда
сходятся и последовательности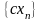
(c-
const),
,
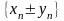и
–
последняя при условии
и
,
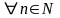– при
этом
а)
,
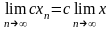б)
(теорема о пределе суммы и разности)
в)
(теорема о пределе произведения)
г)
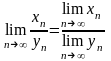(теорема о пределе частного)
7.Предельный переход в неравенствах (для последовательностей).
Лемма
1. Есл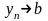и
,
и
,
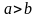то существует такой номер
,
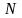что
.
Теорема
2 (о
предельном переходе в неравенстве).
Если
каждая из последовательностей
и
сходится и
,
то
.
Замечание.
Из
того, что
,
и
,
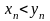в общем случае, следует только, что
,а
не то, что
.
Теорема
3 (принцип
двух милиционеров).
Если
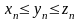,а
последовательности
и
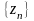сходятся
и имеют один и тот же предел, то сходится
и последовательность
,при
этом.
.
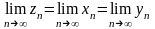Док-во:Пусть
и ,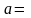
.,
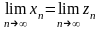(8)
Требуется
доказать, что
(9)
Для
этого выберем произвольное
и покажем, что
такое,
что
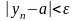.(10)
Поскольку
имеют место равенства (8), то найдется
такой номер
,
что
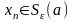и
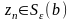,а
так как
,
то отсюда следует, что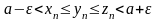
.Следовательно
,что
равносильно (10), а это в силу произвольности
Þ
(9)
8.Монотонные последовательности. Теорема о пределе монотонной последовательности.
Опр1. Последовательность называется
а)
возрастающей,
если,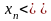
;
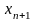б)
неубывающей,
если
;
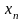в) убывающей, если ;
г)
невозрастающей,
если
;
д) монотонной, если она относится к одному из указанных выше типов а) – г);
е) строго монотонной, если она является либо возрастающей, либо убывающей.
Теорема 1. Всякая ограниченная монотонная последовательность сходится.
Поскольку всякая сходящаяся, и даже необязательно монотонная, последовательность ограничена, то из этой теоремы вытекает такое
Следствие. Для того, чтобы монотонная последовательность была сходящейся, необходимо и достаточно, чтобы она была ограниченной.
Всякая
неубывающая последовательность
,
ограничена
снизу (числом
).
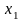Следовательно, для ее ограниченности
достаточно, чтобы она была ограниченной
сверху. Поэтому справедливы следующие
уточнения теорема и ее следствия.
Теорема
2. Всякая
неубывающая,
ограниченная сверху числовая
последовательность
сходится, при этом
Следствие. Для того, чтобы неубывающая числовая последовательность была сходящейся необходимо и достаточно, чтобы она была ограничена сверху.
Аналогично, для невозрастающих последовательностей справедливы следующие утверждения:
Теорема
3. Всякая
невозрастающая,
ограниченная снизу числовая
последовательность
сходится, при этом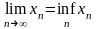
Следствие. Для того, чтобы невозрастающая числовая последовательность была сходящейся необходимо и достаточно, чтобы она была ограничена снизу.
9. Применение теоремы о пределе монотонной последовательности к вычислению пределов.
П
р и м е р 1.
,
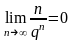если q
> 1.Действительно, здесь
=
,
.
Поэтому
=
,а
так как
=
=
=
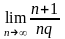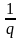
< 1,то найдется номер N,
такой, что при
> N
будем иметь
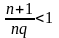и следовательно, при тех же
<
.
Следовательно, если отбросить первые
N
членов рассматриваемой последовательности,
то оставшиеся ее члены будут составлять
монотонно убывающую последовательность,
которая к тому же
ограничена снизу (все ее члены положительные) и в силу этого сходится (теорема 3). Поскольку отбрасывание конечного числа членов последовательности не влияет на ее сходимость, то это означает, что сходится и исходная последовательность.
Найдем
теперь ее предел. Пусть
.
Тогда с учетом равенства (1) будем иметь
=
=
∙
=
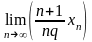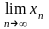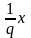.Поэтому
= 0 и, следовательно,
= 0 □
С
л е д с т в и е 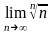1.
= 1.
Д о к а з а т е л ь с т в о. При фиксированном по доказанному в 1-м примере
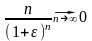(здесь
).
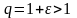Поэтому найдется
такое,
что при
будем иметь ,
и,
следовательно,
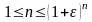при
.А
тогда
при
и
тем более
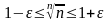при
В силу произвольности это и означает, что = 1 □
С л е д с т в и е 2.
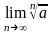= 1
при любом а > 0.,