51.Комплексные числа

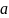Определение 1. Комплексными числами называются всевозможные упорядоченные пары вещественных чисел и 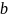, при этом для этих пар понятия равенства, суммы, произведения и отождествления некоторых пар с вещественными числами вводятся по следующим правилам (аксиомам):

I. 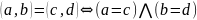(равенство к.ч.)

II. 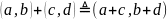(сумма к.ч)

III. 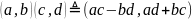(произведение к.ч.)

IV. (отождествление некоторых к.ч с в.ч.)

Множество всех комплексных чисел обозначается буквой .

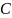Комплексное число

называется противоположным к.ч.

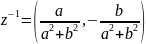
называется обратным к к.ч.

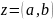
частным от деления к.ч. на к.ч. 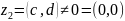называется к.ч.

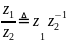
Комплексное число

называется комплексно сопряженным к (для) к.ч.

.

+ .

К.ч. называется мнимой единицей и обозначается буквой

Запись к.ч. в виде

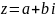
называется алгебраической формой записи этого к.ч

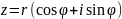
Такая форма записи к.ч. называется тригонометрической формой записи этого к.ч., при этом (заведомо неотрицательное) вещественное число называют модулем к.ч. и обозначают 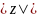, а число 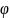называют аргументом к.ч. и обозначают .

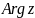14. Частичные пределы. Верхний и нижний пределы.

Определение 2. Число (или символ  или ) называется частичным пределом последовательности , если оно (он) является пределом некоторой ее подпоследовательности. Из теоремы Больцано-Вейерштрасса следует, что всякая числовая последовательность (необязательно ограниченная) имеет хотя бы один (возможно бесконечный) частичный предел. Более того, можно показать, что множество всех частичных пределов всякой числовой последовательности имеет наибольший и наименьший элементы.Определение 3. Наибольший (соотв, наименьший) из частичных пределов ограниченной последовательности называется верхним (соотв., нижним) ее пределом.Верхний и нижний пределы обозначаются , соответственно, символам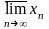и и Пример.Рассмотрим последовательность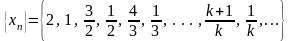 .Легко видеть, что , .

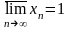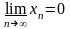50.

Об основных понятиях.

–множество всех натуральных чисел ( N = {1, 2, 3, . . . } );

– множество всех целых чисел ( = {0, ±1, ±2, ±3, . . . } );

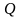– множество всех рациональных чисел, Q = { x | x = p/q, р Z, q N };

– множества всех вещественных чисел.

множество вещественных чисел состоит из всех рациональных чисел и из всех иррациональных чисел. каждое рациональное число можно записать либо в виде конечной десятичной дроби либо в виде периодической бесконечной десятичной дроби

–каждое иррациональное вещественное число отождествляется с бесконечной непериодической десятичной дробью. Таким образом, можно сказать, что множество вещественных чисел это – множество всех десятичных дробей (как конечных, так и бесконечных).

Далее считается известным то, как во множестве вещественных чисел вводятся алгебраические операции сложения и умножения, а также обратные к ним операции вычитания и деления, соответственно; считаются известными также свойства этих операций.

Наконец, далее предполагается известным

а) как во множестве вещественных чисел вводятся отношения :

> - «больше», < - «меньше» ( ),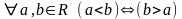

- «больше или равно» - «меньше или равно»;

и каковы свойства этих отношений;

б) что между множеством вещественных чисел и точками той или иной прямой можно установить взаимно-однозначное соответствие и, следовательно, множество вещественных чисел можно отождествить с прямой (поэтому оно часто называется числовой прямой).

Касаясь а) отметим только следующий факт: между любыми двумя различными вещественными числами лежит по крайней мере одно рациональное число (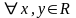 таких, что , : ).

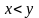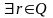Напомним определения некоторых важных подмножеств числовой прямой . Пусть , 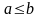. Множество

≜

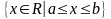
называется отрезком или сегментом (при оно вырождается в точку); множество

≜

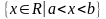
- интервалом (при оно пустое), а множества

≜

≜

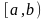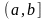- полуинтервалами (при они пустые). Каждое из этих четырех типов множеств называется также промежутком (первое из них иногда называется замкнутым интервалом, а второе – открытым интервалом). Аналогично определяются эти множества и когда 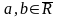. Далее иногда для нас будет неважно с каким из четырех указанных выше типов промежутков мы имеем дело – важно лишь будет, что его концами являются точки , . В таких случаях будем обозначать этот промежуток так: .

Напомним как вводится понятие абсолютной величины (или модуля) 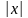вещественного числа и каковы ее свойства. А именно,

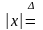
Свойства модуля в.ч.

1^о > 0 .

2^o

3^o .

4^o .

5^о .

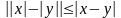Часто бывает удобно дополнить множество вещественных чисел элементами, обозначаемыми и , называемыми соответственно плюс бесконечностью и минус бесконечностью, при этом по определению считается, что

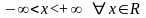
Множество вещественных чисел дополненное элементами и называется расширенным множеством вещественных чисел или расширенной числовой прямой и обозначается (т.о. ).
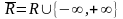