2. Число Рейнольдса. Критерий Рейнольдса. Вязкость. Сила вязкого трения. Течение вязкой жидкости по трубе. Формула Пуазейля.

Re – число Рейнольдса. Re≡ρvl/η – где ρ – плотность среды, v – характерная скорость, l – характерный линейный размер, η — динамическая вязкость среды, ν — кинематическая вязкость среды, м2/с() , Q — объёмная скорость потока, A — площадь сечения трубы.

Число Рейнольдса есть отношение сил инерции, действующих в потоке, к силам вязкости.

Также число Рейнольдса можно рассматривать как отношение кинетической энергии жидкости к потерям энергии на характерной длине.

Критерий Рейнольдса: уравнение Бернулли применимо при Re >> 1

Re≡W_кин/A_трения =(1/2) ρv²(l³)/ηl²(v/l)l; ½ опускаем в связи со знаком >>.

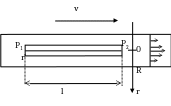Сила вязкого трения. В случае силы сухого трения при силах, меньших силы трения скольжения 2 поверхности не движутся относительно друг друга, а в случае вязкого трения какова бы ни была сила – возникнет движение, причем для малых скоростей сила вязкого трения пропорциональна скорости, а на больших скоростях её квадрату. В общем случае уравнение для силы вязкого трения представляет бесконечный полином.

Течение вязкой жидкости. Формула Пуазейля

Вя́зкость (вну́треннее тре́ние) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. Механизм внутреннего трения в жидкостях и газах заключается в том, что хаотически движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей — это описывается введением силы трения.

Если по горизонтальной трубе постоянного сечения будет протекать реальная жидкость, для которой нельзя пренебречь силами вязкого трения, то давление в трубе не будет постоянным, произойдет перераспределение давления, которое будет существенно зависеть от свойств жидкости (вязкости). Силы вязкости определяется законом Ньютона [1]: тангенциальная сила вязкого трения между движущимися слоями жидкости приходящаяся на единицу площади соприкосновения равна

в этой формуле коэффициент пропорциональности η - полностью определяется свойствами жидкости и называется динамическим коэффициентом вязкости. Вязкость может изменяться в широких пределах, она мала для легко подвижных жидкостей, таких как вода, бензин, эфир, и велика для малоподвижных жидкостей таких как масло, мед, смола и т.д. В целом строгое понятие вязкости вполне соответствует обычным представлениям о вязких и маловязких жидкостях. Модель движущейся жидкости, в рамках которой пренебрегают вязкостью, называется идеальной жидкостью. Для расчета сил вязкого трения, действующих на жидкость необходимо, прежде всего, найти распределение скоростей жидкости внутри трубы (используя закон вязкого трения), после чего можно вычислить силу сопротивления движению, расход жидкости и так далее.

Для круговой цилиндрической трубы эта задача была решена французским физиком Ж. Пуазейлем, который установил, что расход жидкости пропорционален разности давлений на концах трубы Δp, четвертой степени радиуса трубы, обратно пропорционален ее длине: